Bregman–Minc inequality
In discrete mathematics, the Bregman–Minc inequality, or Bregman's theorem, allows one to estimate the permanent of a binary matrix via its row or column sums. The inequality was conjectured in 1963 by Henryk Minc and first proved in 1973 by Lev M. Bregman.[1][2] Further entropy-based proofs have been given by Alexander Schrijver and Jaikumar Radhakrishnan.[3][4] The Bregman–Minc inequality is used, for example, in graph theory to obtain upper bounds for the number of perfect matchings in a bipartite graph.
Statement
The permanent of a square binary matrix [math]\displaystyle{ A = (a_{ij}) }[/math] of size [math]\displaystyle{ n }[/math] with row sums [math]\displaystyle{ r_i = a_{i1} + \cdots + a_{in} }[/math] for [math]\displaystyle{ i=1, \ldots , n }[/math] can be estimated by
- [math]\displaystyle{ \operatorname{per}A \leq \prod_{i=1}^n (r_i!)^{1/r_i}. }[/math]
The permanent is therefore bounded by the product of the geometric means of the numbers from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ r_i }[/math] for [math]\displaystyle{ i=1, \ldots , n }[/math]. Equality holds if the matrix is a block diagonal matrix consisting of matrices of ones or results from row and/or column permutations of such a block diagonal matrix. Since the permanent is invariant under transposition, the inequality also holds for the column sums of the matrix accordingly.[5][6]
Application
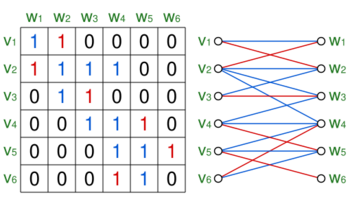
There is a one-to-one correspondence between a square binary matrix [math]\displaystyle{ A }[/math] of size [math]\displaystyle{ n }[/math] and a simple bipartite graph [math]\displaystyle{ G = (V \, \dot\cup \, W, E) }[/math] with equal-sized partitions [math]\displaystyle{ V = \{ v_1, \ldots , v_n \} }[/math] and [math]\displaystyle{ W = \{ w_1, \ldots , w_n \} }[/math] by taking
- [math]\displaystyle{ a_{ij} = 1 \Leftrightarrow \{ v_i, w_j \} \in E. }[/math]
This way, each nonzero entry of the matrix [math]\displaystyle{ A }[/math] defines an edge in the graph [math]\displaystyle{ G }[/math] and vice versa. A perfect matching in [math]\displaystyle{ G }[/math] is a selection of [math]\displaystyle{ n }[/math] edges, such that each vertex of the graph is an endpoint of one of these edges. Each nonzero summand of the permanent of [math]\displaystyle{ A }[/math] satisfying
- [math]\displaystyle{ a_{1\sigma(1)} \cdots a_{n\sigma(n)} = 1 }[/math]
corresponds to a perfect matching [math]\displaystyle{ \{ \{ v_1, w_{\sigma(1)} \}, \ldots , \{ v_n, w_{\sigma(n)} \} \} }[/math] of [math]\displaystyle{ G }[/math]. Therefore, if [math]\displaystyle{ \mathcal{M}(G) }[/math] denotes the set of perfect matchings of [math]\displaystyle{ G }[/math],
- [math]\displaystyle{ | \mathcal{M}(G) | = \operatorname{per}A }[/math]
holds. The Bregman–Minc inequality now yields the estimate
- [math]\displaystyle{ | \mathcal{M}(G) | \leq \prod_{i=1}^n (d(v_i)!)^{1/d(v_i)}, }[/math]
where [math]\displaystyle{ d(v_i) }[/math] is the degree of the vertex [math]\displaystyle{ v_i }[/math]. Due to symmetry, the corresponding estimate also holds for [math]\displaystyle{ d(w_i) }[/math] instead of [math]\displaystyle{ d(v_i) }[/math]. The number of possible perfect matchings in a bipartite graph with equal-sized partitions can therefore be estimated via the degrees of the vertices of any of the two partitions.[7]
Related statements
Using the inequality of arithmetic and geometric means, the Bregman–Minc inequality directly implies the weaker estimate
- [math]\displaystyle{ \operatorname{per}A \leq \prod_{i=1}^n \frac{r_i+1}{2}, }[/math]
which was proven by Henryk Minc already in 1963. Another direct consequence of the Bregman–Minc inequality is a proof of the following conjecture of Herbert Ryser from 1960. Let [math]\displaystyle{ k }[/math] by a divisor of [math]\displaystyle{ n }[/math] and let [math]\displaystyle{ \Lambda_{kn} }[/math] denote the set of square binary matrices of size [math]\displaystyle{ n }[/math] with row and column sums equal to [math]\displaystyle{ k }[/math], then
- [math]\displaystyle{ \max_{A \in \Lambda_{kn}} \operatorname{per}A = (k!)^{n/k}. }[/math]
The maximum is thereby attained for a block diagonal matrix whose diagonal blocks are square matrices of ones of size [math]\displaystyle{ k }[/math]. A corresponding statement for the case that [math]\displaystyle{ k }[/math] is not a divisor of [math]\displaystyle{ n }[/math] is an open mathematical problem.[5][6]
See also
References
- ↑ Henryk Minc (1963), "Upper bounds for permanents of (0,1)-matrices", Bull. Amer. Math. Soc. 69: 789–791, doi:10.1090/s0002-9904-1963-11031-9
- ↑ Lev Bregman (1973), "Some properties of nonnegative matrices and their permanents", Soviet Math. Dokl. 14: 945–949
- ↑ Alexander Schrijver (1978), "A short proof of Minc's conjecture", J. Combin. Theory Ser. A 25: 80–83, doi:10.1016/0097-3165(78)90036-5, https://ir.cwi.nl/pub/7430
- ↑ Jaikumar Radhakrishnan (1997), "An entropy proof of Bregman's theorem", J. Combin. Theory Ser. A 77: 161–164, doi:10.1006/jcta.1996.2727
- ↑ 5.0 5.1 Henryk Minc (1984), Permanents, Encyclopedia of Mathematics and its Applications, 6, Cambridge University Press, pp. 107–109
- ↑ 6.0 6.1 Vladimir Sachkov (1996), Combinatorial Methods in Discrete Mathematics, Cambridge University Press, pp. 95–97
- ↑ Martin Aigner, Günter M. Ziegler (2015), Das Buch der Beweise (4. ed.), Springer, pp. 285–292
External links
- Robin Whitty. "Bregman's Theorem" (PDF; 274 KB). http://www.theoremoftheday.org/CombinatorialTheory/Bregman/TotDBregman.pdf.
 |