False diffusion

Short description: Error in computational fluid dynamics

False diffusion is a type of error observed when the upwind scheme is used to approximate the convection term in convection–diffusion equations. The more accurate central difference scheme can be used for the convection term, but for grids with cell Peclet number more than 2, the central difference scheme is unstable and the simpler upwind scheme is often used. The resulting error from the upwind differencing scheme has a diffusion-like appearance in two- or three-dimensional co-ordinate systems and is referred as "false diffusion". False-diffusion errors in numerical solutions of convection-diffusion problems, in two- and three-dimensions, arise from the numerical approximations of the convection term in the conservation equations. Over the past 20 years many numerical techniques have been developed to solve convection-diffusion equations and none are problem-free, but false diffusion is one of the most serious problems and a major topic of controversy and confusion among numerical analysts.

Definition

False diffusion is defined as an error having a diffusion-like appearance, obtained when the upwind scheme is used in multidimensional cases to solve for the distribution of transported properties flowing non-orthogonally to one or more of the system's major axes. The error is absent when the flow is orthogonal or parallel to each major axis.

Example

Fig 1:Flow domain illustrating false diffusion

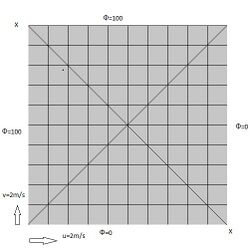
In figure 1, u = 2 and v = 2 m/s everywhere so the velocity field is uniform and perpendicular to the diagonal (XX). The boundary conditions for temperature on north and west wall is 100 ̊C and for east and south wall is 0 ̊C. This region is meshed into 10×10 equal grids. Take two cases, (i) with diffusion coefficient ≠ 0 and, case (ii) with diffusion coefficient = 0.

Case (i)

Fig 2: West face is at 100°C while south wall is at 0°C. Heat is diffused across the diagonal XX

In this case, heat from west and south walls is carried by convection flow towards north and east walls. Heat is also diffused across the diagonal XX from upper to lower triangle. Figure 2 shows the approximate temperature distribution.

Case (ii)

In this case heat from west and south walls is convected by flow towards north and east. There will be no diffusion across the diagonal XX but, when the upwind scheme is applied the results are similar to case (i) where actual diffusion is occurring. This error is known as false diffusion.

Background

In early approaches, derivatives in the differential form of the governing transport equation were replaced by finite difference approximations, usually central differencing approximations with second order accuracy. However, for large Peclet numbers (generally > 2) this approximation gave inaccurate results. It was recognized independently by several investigators that the less expensive but only first order accurate upwind scheme can be employed but that this scheme produces results with false diffusion for multidimensional cases. Many new schemes have been developed to counter false diffusion but a reliable, accurate and economical discretisation scheme is still unavailable.

Reducing errors

Fig 3(a): Mesh size of 8×8

Fig 3(b): Result of upwind scheme with mesh size 8X8

Fig 4(a): Mesh size of 64×64

Fig 4(b): Result of upwind scheme with mesh size 64×64

Finer mesh

False diffusion with the upwind scheme is reduced by increasing the mesh density. In the results of figure 3 and 4 the false diffusion error is lowest in figure 4(b) with finer mesh size.

Other schemes

False diffusion error also can be reduced by using schemes such as the power law scheme, QUICK scheme, exponential scheme, and SUCCA, and others.

Improving the upwind scheme

False diffusion with the simple upwind scheme occurs because the scheme does not take into account grid/flow direction inclination. An approximate expression for the false-diffusion term in two dimensions has been given by de Vahl Davis and Mallinson(1972)

[math]\displaystyle{ {\tau _{fc}^\star= \frac {\rho\ U \,\Delta x \,\Delta y \sin 2\theta}{4(\Delta y \sin ^3 \theta+\Delta x \cos ^3 \theta)}} }[/math]

(1)

where U is the resultant velocity and θ is the angle made by the velocity vector with the x direction. False diffusion is absent when the resultant flow is aligned with either of the sets of grid lines and is greatest when the flow direction is 45˚ to the grid lines.

Determining the accuracy of approximation for the convection term

Using Taylor series for [math]\displaystyle{ \phi_{W} }[/math] and [math]\displaystyle{ \phi_P }[/math] at the time t + kt are

[math]\displaystyle{ \phi_{Wk} = \phi_{wk} - \left(\frac{\delta x_i}{2}\right)\left(\frac{\partial \phi}{\partial x}\right)_{wk}+\frac{1}{2!}\left(\frac{\delta x_i}{2} \right)^2 \left(\frac{\partial^2\phi}{\partial x^2}\right)_{wk} + \cdots. }[/math]

(2a)

[math]\displaystyle{ \phi_{Pk}=\phi_{wk} - \left(\frac{\delta x_i}{2}\right) \left(\frac{\partial \phi}{\partial x}\right)_{wk} + \frac{1}{2!}\left(\frac{\delta x_i}{2} \right)^2 \left(\frac{\partial^2\phi}{\partial x^2}\right)_{wk}+\cdots. }[/math]

(2b)

according to the upwind approximation for convection (UAC),[math]\displaystyle{ {\phi_{wk} = \phi_{Wk}} }[/math]. Neglecting the higher order in equation (2a), the error of convected flux due to this approximation is [math]\displaystyle{ {-\rho_w u_w \delta y_i\left(\frac{\delta x_i}{2} \right) \left( \frac{\partial \phi}{\partial x}\right)_{wk}} }[/math]. It has the form of flux of [math]\displaystyle{ {\phi} }[/math] by false diffusion with a diffusion co-efficient

[math]\displaystyle{ \tau_{fc,UAC}^\star ={\rho_w u_w \left(\frac{\Delta x_i}{2}\right)} }[/math]

(3)

The subscript fc is a reminder that this is a false diffusion arising from the estimate of the convected flux at the instant [math]\displaystyle{ t+k\,\Delta t }[/math] using UAC.

Skew upwind corner convection algorithm (SUCCA)

Fig 5:SUCCA grid cell cluster

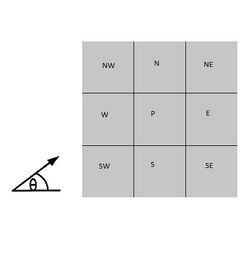
SUCCA takes the local flow direction into account by introducing the influence of upwind corner cells into the discretized conservation equation in the general governing transport equation. In Fig 5, SUCCA is applied within nine cell grid cluster. Considering the SW corner inflow for cell P, the SUCCA equations for the convective transport of the conserved species [math]\displaystyle{ {\phi} }[/math] are

[math]\displaystyle{ C_P \phi _P= \left(\dot m_w - \frac {(\dot m_s)^2} {\dot m_w} \right) \phi_W + \left(\dot m_s + \frac {(\dot m_s) ^2} {\dot m_w} \right)\phi_{SW} + 0.\phi_S\text{ for } 0\lt \theta\le 45 }[/math]

(4)

i.e.,

[math]\displaystyle{ C_P \phi_P = C_w \phi_W + C_sw \phi_{SW} }[/math]

(5)

[math]\displaystyle{ C_P \phi _P= \left(\dot m_s - \frac {(\dot m_w)^2} {\dot m_s} \right)\phi_W +{\left(\dot m_w+ \frac {(\dot m_w) ^2} {\dot m_s} \right) \phi _{SW}} + 0.\phi_W \text{ for }45\lt \theta\lt 90 }[/math]

(6)

i.e.,

[math]\displaystyle{ C_P \phi_P = C_s \phi_S + C_sw \phi_{SW} }[/math]

(7)

This formulation satisfies all the criteria of convergence and stability.

Fig 6: Comparison of different schemes

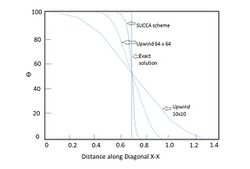
In Fig. 6, as mesh is refined, the upwind scheme gives more accurate results but SUCCA offers a nearly exact solution and is more useful in avoiding multidimensional false diffusion errors.

See also

• Computational fluid dynamics
• Navier–Stokes equations
• Numerical diffusion
• Finite volume method
• Taylor series

Further reading

• Patankar, Suhas V. (1980), Numerical Heat Transfer and Fluid Flow, Taylor & Francis Group, ISBN 9780891165224 
• Wesseling, Pieter (2001), Principles of Computational Fluid Dynamics, Springer, ISBN 978-3-540-67853-3 
• Date, Anil W. (2005), Introduction to Computational Fluid Dynamics, Cambridge University Press, ISBN 9780521853262