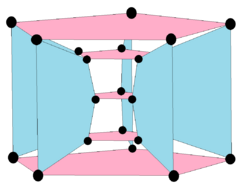
5-5 duoprism

Uniform 5-5 duoprism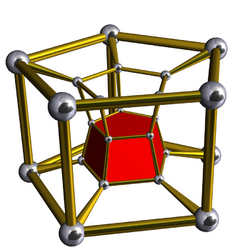 Schlegel diagram
Type	Uniform duoprism
Schläfli symbol	{5}×{5} = {5}2
Coxeter diagram
Cells	10 pentagonal prisms
Faces	25 squares, 10 pentagons
Edges	50
Vertices	25
Vertex figure	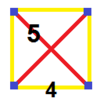Tetragonal disphenoid
Symmetry	[[5,2,5]] = [10,2+,10], order 200
Dual	5-5 duopyramid
Properties	convex, vertex-uniform, facet-transitive

In geometry of 4 dimensions, a 5-5 duoprism or pentagonal duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two pentagons.

It has 25 vertices, 50 edges, 35 faces (25 squares, and 10 pentagons), in 10 pentagonal prism cells. It has Coxeter diagram , and symmetry [[5,2,5]], order 200.

Images

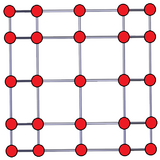Orthogonal projection

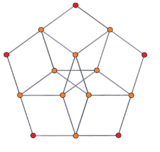Orthogonal projection

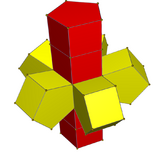Net

Seen in a skew 2D orthogonal projection, 20 of the vertices are in two decagonal rings, while 5 project into the center. The 5-5 duoprism here has an identical 2D projective appearance to the 3D rhombic triacontahedron. In this projection, the square faces project into wide and narrow rhombi seen in penrose tiling.

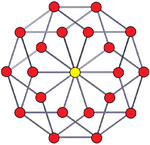
5-5 duoprism	Penrose tiling

Related complex polygons

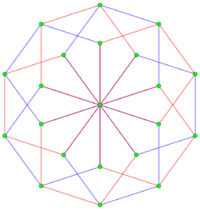
The regular complex polytope ₅{4}₂, , in [math]\displaystyle{ \mathbb{C}^2 }[/math] has a real representation as a 5-5 duoprism in 4-dimensional space. ₅{4}₂ has 25 vertices, and 10 5-edges. Its symmetry is ₅[4]₂, order 50. It also has a lower symmetry construction, , or ₅{}×₅{}, with symmetry ₅[2]₅, order 25. This is the symmetry if the red and blue 5-edges are considered distinct.

Perspective projection of complex polygon, 5{4}2 has 25 vertices and 10 5-edges, shown here with 5 red and 5 blue pentagonal 5-edges.

Orthogonal projection with coinciding central vertices

Orthogonal projection, perspective offset to avoid overlapping elements

Related honeycombs and polytopes

The birectified order-5 120-cell, , constructed by all rectified 600-cells, a 5-5 duoprism vertex figure.

5-5 duopyramid

5-5 duopyramid
Type	Uniform dual duopyramid
Schläfli symbol	{5}+{5} = 2{5}
Coxeter diagram
Cells	25 tetragonal disphenoids
Faces	50 isosceles triangles
Edges	35 (25+10)
Vertices	10 (5+5)
Symmetry	[[5,2,5]] = [10,2+,10], order 200
Dual	5-5 duoprism
Properties	convex, vertex-uniform, facet-transitive

The dual of a 5-5 duoprism is called a 5-5 duopyramid or pentagonal duopyramid. It has 25 tetragonal disphenoid cells, 50 triangular faces, 35 edges, and 10 vertices.

It can be seen in orthogonal projection as a regular 10-gon circle of vertices, divided into two pentagons, seen with colored vertices and edges:

orthogonal projections

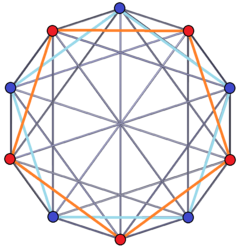Two pentagons in dual positions

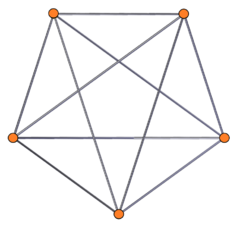Two pentagons overlapping

Related complex polygon

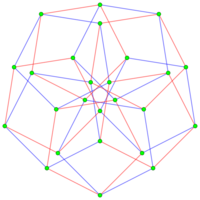
The regular complex polygon ₂{4}₅ has 10 vertices in [math]\displaystyle{ \mathbb{C}^2 }[/math] with a real representation in [math]\displaystyle{ \mathbb{R}^4 }[/math] matching the same vertex arrangement of the 5-5 duopyramid. It has 25 2-edges corresponding to the connecting edges of the 5-5 duopyramid, while the 10 edges connecting the two pentagons are not included. The vertices and edges makes a complete bipartite graph with each vertex from one pentagon is connected to every vertex on the other.

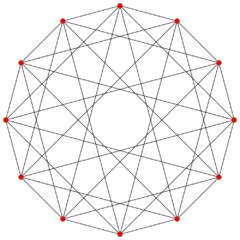Orthographic projection

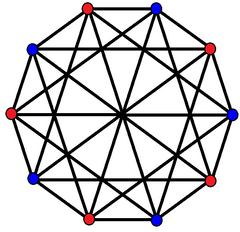The 2{4}5 with 10 vertices in blue and red connected by 25 2-edges as a complete bipartite graph.

See also

• 3-3 duoprism
• 3-4 duoprism
• Tesseract (4-4 duoprism)
• Convex regular 4-polytope
• Duocylinder

References

• Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN:0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
  • Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 (Chapter 26)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• Catalogue of Convex Polychora, section 6, George Olshevsky.

External links

• The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
• Polygloss - glossary of higher-dimensional terms
• Exploring Hyperspace with the Geometric Product