Physics:Undertow (water waves)
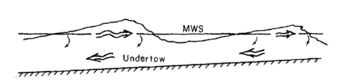
In physical oceanography, undertow is the undercurrent that moves offshore while waves approach the shore. Undertow is a natural and universal feature for almost any large body of water; it is a return flow compensating for the onshore-directed average transport of water by the waves in the zone above the wave troughs. The undertow's flow velocities are generally strongest in the surf zone, where the water is shallow and the waves are high due to shoaling.[1]
In popular usage, the word undertow is often misapplied to rip currents.[2] An undertow occurs everywhere underneath shore-approaching waves, whereas rip currents are localized narrow offshore currents occurring at certain locations along the coast.[3]
Oceanography
An "undertow" is a steady, offshore-directed compensation flow, which occurs below waves near the shore. Physically, nearshore, the wave-induced mass flux between wave crest and trough is onshore directed. This mass transport is localized in the upper part of the water column, i.e. above the wave troughs. To compensate for the amount of water being transported towards the shore, a second-order (i.e. proportional to the wave height squared), offshore-directed mean current takes place in the lower section of the water column. This flow – the undertow – affects the nearshore waves everywhere, unlike rip currents localized at certain positions along the shore.[4]
The term undertow is used in scientific coastal oceanography papers.[5][6][7] The distribution of flow velocities in the undertow over the water column is important as it strongly influences the on- or offshore transport of sediment. Outside the surf zone there is a near-bed onshore-directed sediment transport induced by Stokes drift and skewed-asymmetric wave transport. In the surf zone, strong undertow generates a near-bed offshore sediment transport. These antagonistic flows may lead to sand bar formation where the flows converge near the wave breaking point, or in the wave breaking zone.[5][6][7][8]
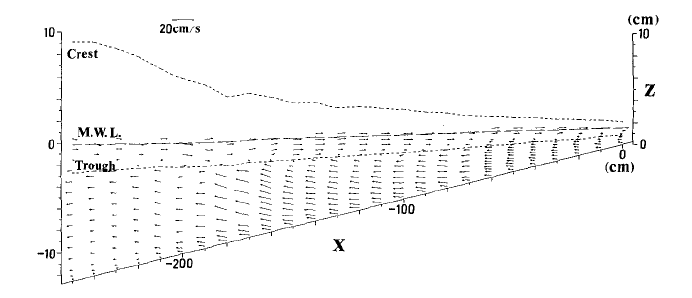
Seaward mass flux
An exact relation for the mass flux of a nonlinear periodic wave on an inviscid fluid layer was established by Levi-Civita in 1924.[9] In a frame of reference according to Stokes' first definition of wave celerity, the mass flux [math]\displaystyle{ M_w }[/math] of the wave is related to the wave's kinetic energy density [math]\displaystyle{ E_k }[/math] (integrated over depth and thereafter averaged over wavelength) and phase speed [math]\displaystyle{ c }[/math] through:
- [math]\displaystyle{ M_w = \frac{2E_k}{c}. }[/math]
Similarly, Longuet Higgins showed in 1975 that – for the common situation of zero mass flux towards the shore (i.e. Stokes' second definition of wave celerity) – normal-incident periodic waves produce a depth- and time-averaged undertow velocity:[10]
- [math]\displaystyle{ \bar{u} = - \frac{2 E_k}{\rho c h}, }[/math]
with [math]\displaystyle{ h }[/math] the mean water depth and [math]\displaystyle{ \rho }[/math] the fluid density. The positive flow direction of [math]\displaystyle{ \bar{u} }[/math] is in the wave propagation direction.
For small-amplitude waves, there is equipartition of kinetic ([math]\displaystyle{ E_k }[/math]) and potential energy ([math]\displaystyle{ E_p }[/math]):
- [math]\displaystyle{ E_w = E_k + E_p \approx 2 E_k \approx 2 E_p, }[/math]
with [math]\displaystyle{ E_w }[/math] the total energy density of the wave, integrated over depth and averaged over horizontal space. Since in general the potential energy [math]\displaystyle{ E_p }[/math] is much easier to measure than the kinetic energy, the wave energy is approximately [math]\displaystyle{ {E_w\approx\tfrac18\rho g H^2} }[/math] (with [math]\displaystyle{ H }[/math] the wave height). So
- [math]\displaystyle{ \bar{u}\approx -\frac18 \frac{g H^2}{ c h }. }[/math]
For irregular waves the required wave height is the root-mean-square wave height [math]\displaystyle{ H_\text{rms}\approx\sqrt{8}\;\sigma, }[/math] with [math]\displaystyle{ \sigma }[/math] the standard deviation of the free-surface elevation.[11] The potential energy is [math]\displaystyle{ E_p=\tfrac12\rho g \sigma^2 }[/math] and [math]\displaystyle{ E_w\approx\rho g \sigma^2. }[/math]
The distribution of the undertow velocity over the water depth is a topic of ongoing research.[5][6][7]
Confusion with rip currents
In contrast to undertow, rip currents are responsible for the great majority of drownings close to beaches. When a swimmer enters a rip current, it starts to carry them offshore. The swimmer can exit the rip current by swimming at right angles to the flow, parallel to the shore, or by simply treading water or floating until the rip releases them. However, drowning can occur when swimmers exhaust themselves by trying unsuccessfully to swim directly against the flow of a rip.
On the United States Lifesaving Association website, it is noted that some uses of the word "undertow" are incorrect:
A rip current is a horizontal current. Rip currents do not pull people under the water—they pull people away from shore. Drowning deaths occur when people pulled offshore are unable to keep themselves afloat and swim to shore. This may be due to any combination of fear, panic, exhaustion, or lack of swimming skills. In some regions, rip currents are referred to by other, incorrect terms such as "rip tides" and "undertow". We encourage exclusive use of the correct term—rip currents. Use of other terms may confuse people and negatively impact public education efforts.[2]
See also
References
Notes
- ↑ Svendsen, I. A. (1984). "Mass flux and undertow in a surf zone". Coastal Engineering Journal 8 (4): 347–365. doi:10.1016/0378-3839(84)90030-9.
- ↑ 2.0 2.1 United States Lifesaving Association Rip Current Survival Guide, United States Lifesaving Association, http://www.usla.org/?page=RIPCURRENTS, retrieved 2014-01-02
- ↑ MacMahan, J. H.; Thornton, E. B.; Reniers, A. J. H. M. (2006). "Rip current review". Coastal Engineering Journal 53 (2): 191–208. doi:10.1016/j.coastaleng.2005.10.009.
- ↑ Lentz, S.J.; Fewings, M.; Howd, P.; Fredericks, J.; Hathaway, K. (2008), "Observations and a Model of Undertow over the Inner Continental Shelf", Journal of Physical Oceanography 38 (11): 2341–2357, doi:10.1175/2008JPO3986.1, Bibcode: 2008JPO....38.2341L
- ↑ 5.0 5.1 5.2 Garcez Faria, A.F.; Thornton, E.B.; Lippman, T.C.; Stanton, T.P. (2000), "Undertow over a barred beach", Journal of Geophysical Research 105 (C7): 16,999–17,010, doi:10.1029/2000JC900084, Bibcode: 2000JGR...10516999F
- ↑ 6.0 6.1 6.2 Haines, J.W.; Sallenger Jr., A.H. (1994), "Vertical structure of mean cross-shore currents across a barred surf zone", Journal of Geophysical Research 99 (C7): 14,223–14,242, doi:10.1029/94JC00427, Bibcode: 1994JGR....9914223H, https://zenodo.org/record/1231343
- ↑ 7.0 7.1 7.2 Reniers, A.J.H.M.; Thornton, E.B.; Stanton, T.P.; Roelvink, J.A. (2004), "Vertical flow structure during Sandy Duck: Observations and modeling", Coastal Engineering 51 (3): 237–260, doi:10.1016/j.coastaleng.2004.02.001
- ↑ Longuet-Higgins, M.S. (1983), "Wave set-up, percolation and undertow in the surf zone", Proceedings of the Royal Society of London A 390 (1799): 283–291, doi:10.1098/rspa.1983.0132, Bibcode: 1983RSPSA.390..283L
- ↑ Levi-Civita, T. (1924), Questioni di meccanica classica e relativista, Bologna: N. Zanichelli, OCLC 441220095, http://mathematica.sns.it/opere/333/
- ↑ Longuet-Higgins, M.S. (1975), "Integral properties of periodic gravity waves of finite amplitude", Proceedings of the Royal Society of London A 342 (1629): 157–174, doi:10.1098/rspa.1975.0018, Bibcode: 1975RSPSA.342..157L
- ↑ Battjes, J.A.; Stive, M.J.F. (1985), "Calibration and verification of a dissipation model for random breaking waves", Journal of Geophysical Research 90 (C5): 9159–9167, doi:10.1029/JC090iC05p09159, Bibcode: 1985JGR....90.9159B, http://resolver.tudelft.nl/uuid:5a03bc35-d87b-464d-b9b9-726fd5b2c624
Other
- Buhr Hansen, J.; Svendsen, I.A. (1984), "A theoretical and experimental study of undertow", in Edge, B.L., Proceedings 19th International Conference on Coastal Engineering, Houston: ASCE, pp. 2246–2262, https://icce-ojs-tamu.tdl.org/icce/index.php/icce/article/viewArticle/3932
- Okayasu, A.; Shibayama, T.; Mimura, N. (1986), "Velocity field under plunging waves", in Edge, B.L., Proceedings of the 20th International Conference on Coastal Engineering, 1, Taipei: ASCE, pp. 660–674, https://icce-ojs-tamu.tdl.org/icce/index.php/icce/article/view/4051
External links
- Tatiana Morales (2004-05-27), Watch out for rip tides, CBS News, http://www.cbsnews.com/stories/2004/05/27/earlyshow/living/main619959.shtml, retrieved 2015-06-24
 |