Bidiakis cube
| bidiakis cube | |
|---|---|
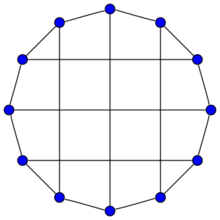 The bidiakis cube | |
| Vertices | 12 |
| Edges | 18 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 4 |
| Automorphisms | 8 (D4) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Cubic Hamiltonian Triangle-free Polyhedral Planar |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the bidiakis cube is a 3-regular graph with 12 vertices and 18 edges.[1]
Construction
The bidiakis cube is a cubic Hamiltonian graph and can be defined by the LCF notation [-6,4,-4]4.
The bidiakis cube can also be constructed from a cube by adding edges across the top and bottom faces which connect the centres of opposite sides of the faces. The two additional edges need to be perpendicular to each other. With this construction, the bidiakis cube is a polyhedral graph, and can be realized as a convex polyhedron. Therefore, by Steinitz's theorem, it is a 3-vertex-connected simple planar graph.[2]
Algebraic properties
The bidiakis cube is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 8, the group of symmetries of a square, including both rotations and reflections.
The characteristic polynomial of the bidiakis cube is [math]\displaystyle{ (x-3)(x-2)(x^4)(x+1)(x+2)(x^2+x-4)^2 }[/math].
Gallery
The chromatic number of the bidiakis cube is 3.
The chromatic index of the bidiakis cube is 3.
The bidiakis cube is a planar graph.
The bidiakis cube constructed from a cube.
References
- ↑ Weisstein, Eric W.. "Bidiakis cube". http://mathworld.wolfram.com/BidiakisCube.html.
- ↑ Branko Grünbaum, Convex Polytopes, 2nd edition, prepared by Volker Kaibel, Victor Klee, and Günter M. Ziegler, 2003, ISBN:0-387-40409-0, ISBN:978-0-387-40409-7, 466pp.
 |
Wikimedia Commons has media related to Bidiakis cube. |
 |  |
