Steinitz's theorem

From HandWiki
Short description: Graph-theoretic description of polyhedra

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.[1]

This result provides a classification theorem for the three-dimensional convex polyhedra, something that is not known in higher dimensions.[2] It provides a complete and purely combinatorial description of the graphs of these polyhedra, allowing other results on them, such as Eberhard's theorem on the realization of polyhedra with given types of faces, to be proven more easily, without reference to the geometry of these shapes.[3] Additionally, it has been applied in graph drawing, as a way to construct three-dimensional visualizations of abstract graphs.[4] Branko Grünbaum has called this theorem "the most important and deepest known result on 3-polytopes."[5]

The theorem appears in a 1922 publication of Ernst Steinitz,[6] after whom it is named. It can be proven by mathematical induction (as Steinitz did), by finding the minimum-energy state of a two-dimensional spring system and lifting the result into three dimensions, or by using the circle packing theorem. Several extensions of the theorem are known, in which the polyhedron that realizes a given graph has additional constraints; for instance, every polyhedral graph is the graph of a convex polyhedron with integer coordinates, or the graph of a convex polyhedron all of whose edges are tangent to a common midsphere.

Definitions and statement of the theorem

Illuminating the skeleton of a convex polyhedron from a light source close to one of its faces causes its shadows to form a planar Schlegel diagram.

An undirected graph is a system of vertices and edges, each edge connecting two of the vertices. As is common in graph theory, for the purposes of Steinitz's theorem these graphs are restricted to being finite (the vertices and edges are finite sets) and simple (no two edges connect the same two vertices, and no edge connects a vertex to itself). From any polyhedron one can form a graph, by letting the vertices of the graph correspond to the vertices of the polyhedron and by connecting any two graph vertices by an edge whenever the corresponding two polyhedron vertices are the endpoints of an edge of the polyhedron. This graph is known as the skeleton of the polyhedron.[7]

A graph is planar if it can be drawn with its vertices as points in the Euclidean plane, and its edges as curves that connect these points, such that no two edge curves cross each other and such that the point representing a vertex lies on the curve representing an edge only when the vertex is an endpoint of the edge. By Fáry's theorem, every planar drawing can be straightened so that the curves representing the edges are line segments. A graph is 3-connected if it has more than three vertices and, after the removal of any two of its vertices, any other pair of vertices remain connected by a path. Steinitz's theorem states that these two conditions are both necessary and sufficient to characterize the skeletons of three-dimensional convex polyhedra: a given graph [math]\displaystyle{ G }[/math] is the graph of a convex three-dimensional polyhedron, if and only if [math]\displaystyle{ G }[/math] is planar and 3-vertex-connected.[5][8]

Proofs

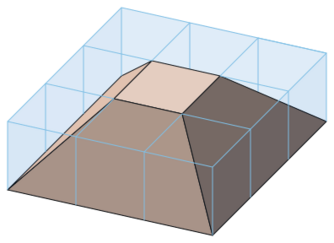
Illustration of the proof of Balinski's theorem, showing the zero set of a linear function (blue) passing through two given vertices (yellow) and the simplex-method paths connecting the remaining graph (green)

One direction of Steinitz's theorem (the easier direction to prove) states that the graph of every convex polyhedron is planar and 3-connected. As shown in the illustration, planarity can be shown by using a Schlegel diagram: if one places a light source near one face of the polyhedron, and a plane on the other side, the shadows of the polyhedron edges will form a planar graph, embedded in such a way that the edges are straight line segments. The 3-connectivity of a polyhedral graph is a special case of Balinski's theorem that the graph of any [math]\displaystyle{ k }[/math]-dimensional convex polytope is [math]\displaystyle{ k }[/math]-connected. The connectivity of the graph of a polytope, after removing any [math]\displaystyle{ k-1 }[/math] of its vertices, can be proven by choosing one more vertex [math]\displaystyle{ v }[/math], finding a linear function that is zero on the resulting set of [math]\displaystyle{ k }[/math] vertices, and following the paths generated by the simplex method to connect every vertex to one of two extreme vertices of the linear function, with the chosen vertex [math]\displaystyle{ v }[/math] connected to both.[9]

The other, more difficult, direction of Steinitz's theorem states that every planar 3-connected graph is the graph of a convex polyhedron. There are three standard approaches for this part: proofs by induction, lifting two-dimensional Tutte embeddings into three dimensions using the Maxwell–Cremona correspondence, and methods using the circle packing theorem to generate a canonical polyhedron.

Induction

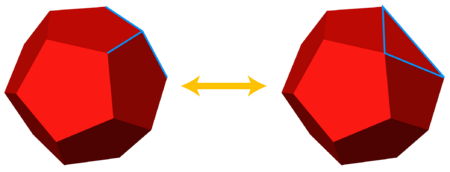
ΔY- and YΔ-transformation of a polyhedron

Although Steinitz's original proof was not expressed in terms of graph theory, it can be rewritten in those terms, and involves finding a sequence of ΔY- and YΔ-transformations that reduce any 3-connected planar graph to [math]\displaystyle{ K_4 }[/math], the graph of the tetrahedron. A YΔ-transformation removes a degree-three vertex from a graph, adding edges between all of its former neighbors if those edges did not already exist; the reverse transformation, a ΔY-transformation, removes the edges of a triangle from a graph and replaces them by a new degree-three vertex adjacent to the same three vertices. Once such a sequence is found, it can be reversed and converted into geometric operations that build up the desired polyhedron step by step starting from a tetrahedron. Each YΔ-transformation in the reversed sequence can be performed geometrically by slicing off a degree-three vertex from a polyhedron. A ΔY-transformation in the reversed sequence can be performed geometrically by removing a triangular face from a polyhedron and extending its neighboring faces until the point where they meet, but only when that triple intersection point of the three neighboring faces is on the far side of the removed face from the polyhedron. When the triple intersection point is not on the far side of this face, a projective transformation of the polyhedron suffices to move it to the correct side. Therefore, by induction on the number of ΔY- and YΔ-transformations needed to reduce a given graph to [math]\displaystyle{ K_4 }[/math], every polyhedral graph can be realized as a polyhedron.[5]

A later work by Epifanov strengthened Steinitz's proof that every polyhedral graph can be reduced to [math]\displaystyle{ K_4 }[/math] by ΔY- and YΔ-transformations. Epifanov proved that if two vertices are specified in a planar graph, then the graph can be reduced to a single edge between those terminals by combining ΔY- and YΔ-transformations with series–parallel reductions.[10] Epifanov's proof was complicated and non-constructive, but it was simplified by Truemper using methods based on graph minors. Truemper observed that every grid graph is reducible by ΔY- and YΔ-transformations in this way, that this reducibility is preserved by graph minors, and that every planar graph is a minor of a grid graph.[11] This idea can be used to replace Steinitz's lemma that a reduction sequence exists. After this replacement, the rest of the proof can be carried out using induction in the same way as Steinitz's original proof.[8] For these proofs, carried out using any of the ways of finding sequences of ΔY- and YΔ-transformations, there exist polyhedral graphs that require a nonlinear number of steps. More precisely, every planar graph can be reduced using a number of steps at most proportional to [math]\displaystyle{ n^{3/2} }[/math], and infinitely many graphs require a number of steps at least proportional to [math]\displaystyle{ n^{3/2} }[/math], where [math]\displaystyle{ n }[/math] is the number of vertices in the graph.[12][13]

An alternative form of induction proof is based on removing edges (and compressing out the degree-two vertices that might be left after this removal) or contracting edges and forming a minor of the given planar graph. Any polyhedral graph can be reduced to [math]\displaystyle{ K_4 }[/math] by a linear number of these operations, and again the operations can be reversed and the reversed operations performed geometrically, giving a polyhedral realization of the graph. However, while it is simpler to prove that a reduction sequence exists for this type of argument, and the reduction sequences are shorter, the geometric steps needed to reverse the sequence are more complicated.[14]

Lifting

Equilibrium stress on the graph of a cube
A frustum lifting the stressed drawing (with the same 2d positions) into 3d

If a graph is drawn in the plane with straight line edges, then an equilibrium stress is defined as an assignment of nonzero real numbers (weights) to the edges, with the property that each vertex is in the position given by the weighted average of its neighbors. According to the Maxwell–Cremona correspondence, an equilibrium stress can be lifted to a piecewise linear continuous three-dimensional surface such that the edges forming the boundaries between the flat parts of the surface project to the given drawing. The weight and length of each edge determines the difference in slopes of the surface on either side of the edge, and the condition that each vertex is in equilibrium with its neighbors is equivalent to the condition that these slope differences cause the surface to meet up with itself correctly in the neighborhood of the vertex. Positive weights translate to convex dihedral angles between two faces of the piecewise linear surface, and negative weights translate to concave dihedral angles. Conversely, every continuous piecewise-linear surface comes from an equilibrium stress in this way. If a finite planar graph is drawn and given an equilibrium stress in such a way that all interior edges of the drawing have positive weights, and all exterior edges have negative weights, then by translating this stress into a three-dimensional surface in this way, and then replacing the flat surface representing the exterior of the graph by its complement in the same plane, one obtains a convex polyhedron, with the additional property that its perpendicular projection onto the plane has no crossings.[15][16]

The Maxwell–Cremona correspondence has been used to obtain polyhedral realizations of polyhedral graphs by combining it with a planar graph drawing method of W. T. Tutte, the Tutte embedding. Tutte's method begins by fixing one face of a polyhedral graph into convex position in the plane. This face will become the outer face of a drawing of a graph. The method continues by setting up a system of linear equations in the vertex coordinates, according to which each remaining vertex should be placed at the average of its neighbors. Then as Tutte showed, this system of equations will have a unique solution in which each face of the graph is drawn as a convex polygon.[17] Intuitively, this solution describes the pattern that would be obtained by replacing the interior edges of the graph by ideal springs and letting them settle to their minimum-energy state.[18] The result is almost an equilibrium stress: if one assigns weight one to each interior edge, then each interior vertex of the drawing is in equilibrium. However, it is not always possible to assign negative numbers to the exterior edges so that they, too, are in equilibrium. Such an assignment is always possible when the outer face is a triangle, and so this method can be used to realize any polyhedral graph that has a triangular face. If a polyhedral graph does not contain a triangular face, its dual graph does contain a triangle and is also polyhedral, so one can realize the dual in this way and then realize the original graph as the polar polyhedron of the dual realization.[4][19] An alternative method for realizing polyhedra using liftings avoids duality by choosing any face with at most five vertices as the outer face. Every polyhedral graph has such a face, and by choosing the fixed shape of this face more carefully, the Tutte embedding of the rest of the graph can be lifted.[20]

Circle packing

A polyhedron realized from a circle packing on the blue midsphere. Each polyhedron vertex is represented in the packing by its horizon circle (red). Each face is represented by the circle made by its intersection with the sphere.

According to one variant of the circle packing theorem, for every polyhedral graph, there exists a system of circles in the plane or on any sphere, representing the vertices and faces of the graph, so that:

  • each two adjacent vertices of the graph are represented by tangent circles,
  • each two adjacent faces of the graph are represented by tangent circle,
  • each pair of a vertex and a face that it touches are represented by circles that cross at a right angle, and
  • all other pairs of circles are separated from each other.[21]

The same system of circles forms a representation of the dual graph by swapping the roles of circles that represent vertices, and circles that represent faces. From any such representation on a sphere, embedded into three-dimensional Euclidean space, one can form a convex polyhedron that is combinatorially equivalent to the given graph, as an intersection of half-spaces whose boundaries pass through the face circles. From each vertex of this polyhedron, the horizon on the sphere, seen from that vertex, is the circle that represents it. This horizon property determines the three-dimensional position of each vertex, and the polyhedron can be equivalently defined as the convex hull of the vertices, positioned in this way. The sphere becomes the midsphere of the realization: each edge of the polyhedron is tangent to the sphere, at a point where two tangent vertex circles cross two tangent face circles.[22]

Realizations with additional properties

Integer coordinates

It is possible to prove a stronger form of Steinitz's theorem, that any polyhedral graph can be realized by a convex polyhedron whose coordinates are integers.[23] For instance, Steinitz's original induction-based proof can be strengthened in this way. However, the integers that would result from Steinitz's construction are doubly exponential in the number of vertices of the given polyhedral graph. Writing down numbers of this magnitude in binary notation would require an exponential number of bits.[19] Geometrically, this means that some features of the polyhedron may have size doubly exponentially larger than others, making the realizations derived from this method problematic for applications in graph drawing.[4]

Subsequent researchers have found lifting-based realization algorithms that use only a linear number of bits per vertex.[20][24] It is also possible to relax the requirement that the coordinates be integers, and assign coordinates in such a way that the [math]\displaystyle{ x }[/math]-coordinates of the vertices are distinct integers in the range from 0 to [math]\displaystyle{ 2n-4 }[/math] and the other two coordinates are real numbers in the unit interval, so that each edge has length at least one while the overall polyhedron has linear volume.[25][26] Some polyhedral graphs are known to be realizable on grids of only polynomial size; in particular this is true for the pyramids (realizations of wheel graphs), prisms (realizations of prism graphs), and stacked polyhedra (realizations of Apollonian networks).[27]

Another way of stating the existence of integer realizations is that every three-dimensional convex polyhedron has a combinatorially equivalent integer polyhedron.[23] For instance, the regular dodecahedron is not itself an integer polyhedron, because of its regular pentagon faces, but it can be realized as an equivalent integer pyritohedron.[20] This is not always possible in higher dimensions, where there exist polytopes (such as the ones constructed from the Perles configuration) that have no integer equivalent.[28]

Equal slopes

A Halin graph is a special case of a polyhedral graph, formed from a planar-embedded tree (with no degree-two vertices) by connecting the leaves of the tree into a cycle. For Halin graphs, one can choose polyhedral realizations of a special type: the outer cycle forms a horizontal convex base face, and every other face lies directly above the base face (as in the polyhedra realized through lifting), with all of these upper faces having the same slope. Polyhedral surfaces with equal-slope faces over any base polygon (not necessarily convex) can be constructed from the polygon's straight skeleton, and an equivalent way of describing this realization is that the two-dimensional projection of the tree onto the base face forms its straight skeleton. The proof of this result uses induction: any rooted tree may reduced to a smaller tree by removing the leaves from an internal node whose children are all leaves, the Halin graph formed from the smaller tree has a realization by the induction hypothesis, and it is possible to modify this realization in order to add any number of leaf children to the tree node whose children were removed.[29]

Specifying the shape of a face

In any polyhedron that represents a given polyhedral graph [math]\displaystyle{ G }[/math], the faces of [math]\displaystyle{ G }[/math] are exactly the cycles in [math]\displaystyle{ G }[/math] that do not separate [math]\displaystyle{ G }[/math] into two components: that is, removing a facial cycle from [math]\displaystyle{ G }[/math] leaves the rest of [math]\displaystyle{ G }[/math] as a connected subgraph. Such cycles are called peripheral cycles. Thus, the combinatorial structure of the faces (but not their geometric shapes) is uniquely determined from the graph structure. Another strengthening of Steinitz's theorem, by Barnette and Grünbaum, states that for any polyhedral graph, any face of the graph, and any convex polygon representing that face, it is possible to find a polyhedral realization of the whole graph that has the specified shape for the designated face. This is related to a theorem of Tutte, that any polyhedral graph can be drawn in the plane with all faces convex and any specified shape for its outer face. However, the planar graph drawings produced by Tutte's method do not necessarily lift to convex polyhedra. Instead, Barnette and Grünbaum prove this result using an inductive method.[30] It is also always possible, given a polyhedral graph [math]\displaystyle{ G }[/math] and an arbitrary cycle [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math], to find a realization for which [math]\displaystyle{ C }[/math] forms the silhouette of the realization under parallel projection.[31]

Tangent spheres

The realization of polyhedra using the circle packing theorem provides another strengthening of Steinitz's theorem: every 3-connected planar graph may be represented as a convex polyhedron in such a way that all of its edges are tangent to the same unit sphere, the midsphere of the polyhedron.[22] By performing a carefully chosen Möbius transformation of a circle packing before transforming it into a polyhedron, it is possible to find a polyhedral realization that realizes all the symmetries of the underlying graph, in the sense that every graph automorphism is a symmetry of the polyhedral realization.[32][33] More generally, if [math]\displaystyle{ G }[/math] is a polyhedral graph and [math]\displaystyle{ K }[/math] is any smooth three-dimensional convex body, it is possible to find a polyhedral representation of [math]\displaystyle{ G }[/math] in which all edges are tangent to [math]\displaystyle{ K }[/math].[34]

Circle packing methods can also be used to characterize the graphs of polyhedra that have a circumsphere through all their vertices, or an insphere tangent to all of their faces. (The polyhedra with a circumsphere are also significant in hyperbolic geometry as the ideal polyhedra.) In both cases, the existence of a sphere is equivalent to the solvability of a system of linear inequalities on positive real variables associated with each edge of the graph. In the case of the insphere, these variables must sum to exactly one on each face cycle of the graph, and to more than one on each non-face cycle. Dually, for the circumsphere, the variables must sum to one at each vertex, and more than one across each cut with two or more vertices on each side of the cut. Although there may be exponentially many linear inequalities to satisfy, a solution (if one exists) can be found in polynomial time using the ellipsoid method. The values of the variables from a solution determine the angles between pairs of circles in a circle packing whose corresponding polyhedron has the desired relation to its sphere.[35][36]

Related results

The graphs of three-dimensional non-convex polyhedra might not be connected (left), and even for topologically spherical polyhedra whose faces are simple polygons these graphs might not be 3-connected (right).[37]

In any dimension higher than three, the algorithmic Steinitz problem consists of determining whether a given lattice is the face lattice of a convex polytope. It is unlikely to have polynomial time complexity, as it is NP-hard and more strongly complete for the existential theory of the reals, even for four-dimensional polytopes, by Richter-Gebert's universality theorem.[38] Here, the existential theory of the reals is a class of computational problems that can be formulated in terms of finding real variables that satisfy a given system of polynomial equations and inequalities. For the algorithmic Steinitz problem, the variables of such a problem can be the vertex coordinates of a polytope, and the equations and inequalities can be used to specify the flatness of each face in the given face lattice and the convexity of each angle between faces. Completeness means that every other problem in this class can be transformed into an equivalent instance of the algorithmic Steinitz problem, in polynomial time. The existence of such a transformation implies that, if the algorithmic Steinitz problem has a polynomial time solution, then so does every problem in the existential theory of the reals, and every problem in NP.[39] However, because a given graph may correspond to more than one face lattice, it is difficult to extend this completeness result to the problem of recognizing the graphs of 4-polytopes. Determining the computational complexity of this graph recognition problem remains open.[40]

Researchers have also found graph-theoretic characterizations of the graphs of certain special classes of three-dimensional non-convex polyhedra[37][41] and four-dimensional convex polytopes.[40][42][43] However, in both cases, the general problem remains unsolved. Indeed, even the problem of determining which complete graphs are the graphs of non-convex polyhedra (other than [math]\displaystyle{ K_4 }[/math] for the tetrahedron and [math]\displaystyle{ K_7 }[/math] for the Császár polyhedron) remains unsolved.[44]

Eberhard's theorem partially characterizes the multisets of polygons that can be combined to form the faces of a convex polyhedron. It can be proven by forming a 3-connected planar graph with the given set of polygon faces, and then applying Steinitz's theorem to find a polyhedral realization of that graph.[3]

László Lovász has shown a correspondence between polyhedral representations of graphs and matrices realizing the Colin de Verdière graph invariants of the same graphs. The Colin de Verdière invariant is the maximum corank of a weighted adjacency matrix of the graph, under some additional conditions that are irrelevant for polyhedral graphs. These are square symmetric matrices indexed by the vertices, with the weight of vertex [math]\displaystyle{ i }[/math] in the diagonal coefficient [math]\displaystyle{ M_{i,i} }[/math] and with the weight of edge [math]\displaystyle{ i,j }[/math] in the off-diagonal coefficients [math]\displaystyle{ M_{i,j} }[/math] and [math]\displaystyle{ M_{j,i} }[/math]. When vertices [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] are not adjacent, the coefficient [math]\displaystyle{ M_{i,j} }[/math] is required to be zero. This invariant is at most three if and only if the graph is a planar graph. As Lovász shows, when the graph is polyhedral, a representation of it as a polyhedron can be obtained by finding a weighted adjacency matrix of corank three, finding three vectors forming a basis for its nullspace, using the coefficients of these vectors as coordinates for the vertices of a polyhedron, and scaling these vertices appropriately.[45]

History

The history of Steinitz's theorem is described by (Grünbaum 2007),[46] who notes its first appearance in a cryptic form in a publication of Ernst Steinitz, originally written in 1916.[6] Steinitz provided more details in later lecture notes, published after his 1928 death. Although modern treatments of Steinitz's theorem state it as a graph-theoretic characterization of polyhedra, Steinitz did not use the language of graphs.[46] The graph-theoretic formulation of the theorem was introduced in the early 1960s by Branko Grünbaum and Theodore Motzkin, with its proof also converted to graph theory in Grünbaum's 1967 text Convex Polytopes.[46] The work of Epifanov on ΔY- and YΔ-transformations, strengthening Steinitz's proof, was motivated by other problems than the characterization of polyhedra. (Truemper 1989) credits Grünbaum with observing the relevance of this work for Steinitz's theorem.[11]

The Maxwell-Cremona correspondence between stress diagrams and polyhedral liftings was developed in a series of papers by James Clerk Maxwell from 1864 to 1870, based on earlier work of Pierre Varignon, William Rankine, and others, and was popularized in the late 19th century by Luigi Cremona.[47] The observation that this correspondence can be used with the Tutte embedding to prove Steinitz's theorem comes from (Eades Garvan);[4] see also (Richter-Gebert 1996).[38]

The circle packing theorem was proved by Paul Koebe in 1936[48][49] and (independently) by E. M. Andreev in 1970;[49][50] it was popularized in the mid-1980s by William Thurston, who (despite citing Koebe and Andreev) is often credited as one of its discoverers.[49] Andreev's version of the theorem was already formulated as a Steinitz-like characterization for certain polyhedra in hyperbolic space,[50] and the use of circle packing to realize polyhedra with midspheres comes from the work of Thurston.[51] The problem of characterizing polyhedra with inscribed or circumscribed spheres, eventually solved using a method based on circle packing realizations, goes back to unpublished work of René Descartes circa 1630[52] and to Jakob Steiner in 1832;[35][53] the first examples of polyhedra that have no realization with a circumsphere or insphere were given by Steinitz in 1928.[35][54]

References

  1. ↑ Weisstein, Eric W.. "Polyhedral graph". http://mathworld.wolfram.com/PolyhedralGraph.html. 
  2. ↑ "Boundary complexes of convex polytopes cannot be characterized locally", Journal of the London Mathematical Society, Second Series 35 (2): 314–326, 1987, doi:10.1112/jlms/s2-35.2.314 
  3. ↑ 3.0 3.1 Malkevitch, Joseph, "Techniques for proving combinatorial theorems about 3-polytopes", Geometric Structures (course notes) (City University of New York), https://www.york.cuny.edu/~malk/geometricstructures/steinitz.html 
  4. ↑ 4.0 4.1 4.2 4.3 Brandenburg, Franz-Josef, ed. (1995), "Drawing stressed planar graphs in three dimensions", Graph Drawing, Symposium on Graph Drawing, GD '95, Passau, Germany, September 20-22, 1995, Proceedings, Lecture Notes in Computer Science, 1027, Springer, pp. 212–223, doi:10.1007/BFb0021805 
  5. ↑ 5.0 5.1 5.2 "13.1 Steinitz's theorem", Convex Polytopes, Graduate Texts in Mathematics, 221 (2nd ed.), Springer-Verlag, 2003, pp. 235–244, ISBN 0-387-40409-0 
  6. ↑ 6.0 6.1 "IIIAB12: Polyeder und Raumeinteilungen" (in de), Encyclopädie der mathematischen Wissenschaften, Band 3 (Geometries), 1922, pp. 1–139, https://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=PPN360609767&DMDID=dmdlog203, "Abgeschlossen am 31. August 1916" 
  7. ↑ More technically, this graph is the 1-skeleton; see (Grünbaum 2003), p. 138, and (Ziegler 1995), p. 64.
  8. ↑ 8.0 8.1 "Chapter 4: Steinitz' Theorem for 3-Polytopes", Lectures on Polytopes, Graduate Texts in Mathematics, 152, Springer-Verlag, 1995, pp. 103–126, ISBN 0-387-94365-X 
  9. ↑ "On the graph structure of convex polyhedra in n-space", Pacific Journal of Mathematics 11 (2): 431–434, 1961, doi:10.2140/pjm.1961.11.431, https://projecteuclid.org/euclid.pjm/1103037323 
  10. ↑ Epifanov, G. V. (1966), "Reduction of a plane graph to an edge by star-triangle transformations" (in ru), Doklady Akademii Nauk SSSR 166: 19–22, http://mi.mathnet.ru/dan31994 
  11. ↑ 11.0 11.1 Truemper, K. (1989), "On the delta-wye reduction for planar graphs", Journal of Graph Theory 13 (2): 141–148, doi:10.1002/jgt.3190130202 
  12. ↑ Aranguri, Santiago; Chang, Hsien-Chih; Fridman, Dylan (2022), "Untangling planar graphs and curves by staying positive", Proceedings of the 2022 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), SIAM, pp. 211–225, doi:10.1137/1.9781611977073.11 
  13. ↑ Chang, Hsien-Chih; Erickson, Jeff (2017), "Untangling planar curves", Discrete & Computational Geometry 58 (4): 889–920, doi:10.1007/s00454-017-9907-6 
  14. ↑ Barnette, David W. (1969), "On Steinitz's theorem concerning convex 3-polytopes and on some properties of planar graphs", The Many Facets of Graph Theory: Proceedings of the Conference held at Western Michigan University, Kalamazoo, MI., October 31 – November 2, 1968, Lecture Notes in Mathematics, 110, Springer, pp. 27–40, doi:10.1007/BFb0060102 
  15. ↑ "On reciprocal figures and diagrams of forces", Philosophical Magazine, 4th Series 27 (182): 250–261, 1864, doi:10.1080/14786446408643663 
  16. ↑ "Motions and stresses of projected polyhedra", Structural Topology 7: 13–38, 1982 
  17. ↑ "How to draw a graph", Proceedings of the London Mathematical Society 13: 743–767, 1963, doi:10.1112/plms/s3-13.1.743 
  18. ↑ Kaufmann, Michael, ed. (2001), "Drawing on physical analogies", Drawing Graphs: Methods and Models, Lecture Notes in Computer Science, 2025, Berlin: Springer, pp. 71–86, doi:10.1007/3-540-44969-8_4 
  19. ↑ 19.0 19.1 Onn, Shmuel (1994), "A quantitative Steinitz' theorem", Beiträge zur Algebra und Geometrie 35 (1): 125–129, https://emis.de/journals/BAG/vol.35/no.1/b35h1onb.ps.gz 
  20. ↑ 20.0 20.1 20.2 Ribó Mor, Ares; Rote, Günter; Schulz, André (2011), "Small grid embeddings of 3-polytopes", Discrete & Computational Geometry 45 (1): 65–87, doi:10.1007/s00454-010-9301-0 
  21. ↑ "Representations of planar graphs", SIAM Journal on Discrete Mathematics 6 (2): 214–229, 1993, doi:10.1137/0406017 
  22. ↑ 22.0 22.1 Miller, Ezra; Reiner, Victor, eds. (2007), "Convex polytopes: extremal constructions and f-vector shapes. Section 1.3: Steinitz's theorem via circle packings", Geometric Combinatorics, IAS/Park City Mathematics Series, 13, American Mathematical Society, pp. 628–642, ISBN 978-0-8218-3736-8 
  23. ↑ 23.0 23.1 (Grünbaum 2003), theorem 13.2.3, p. 244, states this in an equivalent form where the coordinates are rational numbers.
  24. ↑ Buchin, Kevin; Schulz, André (2010), "On the number of spanning trees a planar graph can have", Algorithms - ESA 2010, 18th Annual European Symposium, Liverpool, UK, September 6-8, 2010, Proceedings, Part I, Lecture Notes in Computer Science, 6346, Springer, pp. 110–121, doi:10.1007/978-3-642-15775-2_10, ISBN 978-3-642-15774-5 
  25. ↑ Chrobak, Marek (1996), "Convex drawings of graphs in two and three dimensions", Proceedings of the 12th ACM Symposium on Computational Geometry (SoCG '96), ACM, pp. 319–328, doi:10.1145/237218.237401 
  26. ↑ Schulz, André (2011), "Drawing 3-polytopes with good vertex resolution", Journal of Graph Algorithms and Applications 15 (1): 33–52, doi:10.7155/jgaa.00216 
  27. ↑ "Embedding stacked polytopes on a polynomial-size grid", Discrete & Computational Geometry 57 (4): 782–809, 2017, doi:10.1007/s00454-017-9887-6 
  28. ↑ Grünbaum (2003), p. 96a.
  29. ↑ Aichholzer, Oswin; Cheng, Howard (2012), "What makes a Tree a Straight Skeleton?", Proceedings of the 24th Canadian Conference on Computational Geometry (CCCG'12), http://2012.cccg.ca/papers/paper30.pdf 
  30. ↑ Barnette, David W. (1970), "Preassigning the shape of a face", Pacific Journal of Mathematics 32 (2): 299–306, doi:10.2140/pjm.1970.32.299, http://projecteuclid.org/euclid.pjm/1102977361 
  31. ↑ Barnette, David W. (1970), "Projections of 3-polytopes", Israel Journal of Mathematics 8 (3): 304–308, doi:10.1007/BF02771563 
  32. ↑ "Calculating canonical polyhedra", Mathematica in Education and Research 6 (3): 5–10, 1997, http://library.wolfram.com/infocenter/Articles/2012/ 
  33. ↑ Bern, Marshall W. (2001), "Optimal Möbius transformations for information visualization and meshing", in Dehne, Frank K. H. A.; Sack, Jörg-Rüdiger; Tamassia, Roberto, Algorithms and Data Structures, 7th International Workshop, WADS 2001, Providence, RI, USA, August 8-10, 2001, Proceedings, Lecture Notes in Computer Science, 2125, Springer, pp. 14–25, doi:10.1007/3-540-44634-6_3 
  34. ↑ "How to cage an egg", Inventiones Mathematicae 107 (3): 543–560, 1992, doi:10.1007/BF01231901, Bibcode: 1992InMat.107..543S 
  35. ↑ 35.0 35.1 35.2 "A characterization of ideal polyhedra in hyperbolic 3-space", Annals of Mathematics, Second Series 143 (1): 51–70, 1996, doi:10.2307/2118652 
  36. ↑ Dillencourt, Michael B.; Smith, Warren D. (1996), "Graph-theoretical conditions for inscribability and Delaunay realizability", Discrete Mathematics 161 (1–3): 63–77, doi:10.1016/0012-365X(95)00276-3, https://escholarship.org/uc/item/0hf4118d 
  37. ↑ 37.0 37.1 "Steinitz theorems for simple orthogonal polyhedra", Journal of Computational Geometry 5 (1): 179–244, 2014, doi:10.20382/jocg.v5i1a10 
  38. ↑ 38.0 38.1 Richter-Gebert, Jürgen (1996), Realization Spaces of Polytopes, Lecture Notes in Mathematics, 1643, Springer-Verlag, doi:10.1007/BFb0093761, ISBN 978-3-540-62084-6 
  39. ↑ Schaefer, Marcus (2013), "Realizability of graphs and linkages", Thirty Essays on Geometric Graph Theory, New York: Springer, pp. 461–482, doi:10.1007/978-1-4614-0110-0_24 
  40. ↑ 40.0 40.1 "Treetopes and their graphs", Discrete & Computational Geometry 64 (2): 259–289, 2020, doi:10.1007/s00454-020-00177-0 
  41. ↑ "Extending Steinitz's theorem to upward star-shaped polyhedra and spherical polyhedra", Algorithmica 61 (4): 1022–1076, 2011, doi:10.1007/s00453-011-9570-x 
  42. ↑ "Puzzles and polytope isomorphisms", Aequationes Mathematicae 34 (2–3): 287–297, 1987, doi:10.1007/BF01830678 
  43. ↑ "A simple way to tell a simple polytope from its graph", Journal of Combinatorial Theory, Series A 49 (2): 381–383, 1988, doi:10.1016/0097-3165(88)90064-7 
  44. ↑ "Polyhedral surfaces of high genus", Discrete Differential Geometry, Oberwolfach Seminars, 38, Springer, 2008, pp. 191–213, doi:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7 
  45. ↑ "Steinitz representations of polyhedra and the Colin de Verdière number", Journal of Combinatorial Theory, Series B 82 (2): 223–236, 2001, doi:10.1006/jctb.2000.2027 
  46. ↑ 46.0 46.1 46.2 "Graphs of polyhedra; polyhedra as graphs", Discrete Mathematics 307 (3–5): 445–463, 2007, doi:10.1016/j.disc.2005.09.037 
  47. ↑ Erickson, Jeff; Lin, Patrick (2020), "A toroidal Maxwell–Cremona-Delaunay correspondence", in Cabello, Sergio; Chen, Danny Z., 36th International Symposium on Computational Geometry (SoCG 2020), Leibniz International Proceedings in Informatics (LIPIcs), 164, Dagstuhl, Germany: Schloss Dagstuhl–Leibniz-Zentrum für Informatik, pp. 40:1–40:17, doi:10.4230/LIPIcs.SoCG.2020.40, ISBN 978-3-95977-143-6 
  48. ↑ "Kontaktprobleme der Konformen Abbildung" (in de), Berichte über die Verhandlungen der Sächsischen Akademie der Wissenschaften zu Leipzig: Mathematisch-Physische Klasse 88: 141–164, 1936 
  49. ↑ 49.0 49.1 49.2 Stephenson, Kenneth (2003), "Circle packing: a mathematical tale", Notices of the American Mathematical Society 50 (11): 1376–1388, https://www.ams.org/notices/200311/fea-stephenson.pdf 
  50. ↑ 50.0 50.1 Andreev, E. M. (1970), "Convex polyhedra in Lobačevskiĭ spaces", Matematicheskii Sbornik 81 (123): 445–478, doi:10.1070/SM1970v010n03ABEH001677, Bibcode: 1970SbMat..10..413A, http://mi.mathnet.ru/msb3382 
  51. ↑ "Existence and uniqueness of packings with specified combinatorics", Israel Journal of Mathematics 73 (3): 321–341, 1991, doi:10.1007/BF02773845 ; see discussion following Corollary 3.8, p. 329
  52. ↑ Descartes on Polyhedra: A Study of the "De solidorum elementis", Sources in the History of Mathematics and Physical Sciences, 4, Springer, 1982, p. 52 
  53. ↑ "Question 77" (in de), Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einander, Berlin: G. Fincke, 1832, p. 316, https://archive.org/details/systematischeen02steigoog/page/n343 
  54. ↑ Steinitz, Ernst (1928), "Über isoperimetrische Probleme bei konvexen Polyedern" (in de), Journal für die Reine und Angewandte Mathematik 1928 (159): 133–143, doi:10.1515/crll.1928.159.133 



Retrieved from "https://handwiki.org/wiki/index.php?title=Steinitz%27s_theorem&oldid=3371523"