Pseudo amino acid composition
Pseudo amino acid composition, or PseAAC, in molecular biology, was originally introduced by Kuo-Chen Chou in 2001 to represent protein samples for improving protein subcellular localization prediction and membrane protein type prediction.[1] Like the vanilla amino acid composition (AAC) method, it characterizes the protein mainly using a matrix of amino-acid frequencies, which helps with dealing with proteins without significant sequential homology to other proteins. Compared to AAC, additional information are also included in the matrix to represent some local features, such as correlation between residues of a certain distance.[2] When dealing the cases of PseAAC, the Chou's invariance theorem has been often used.
Background
To predict the subcellular localization of proteins and other attributes based on their sequence, two kinds of models are generally used to represent protein samples: (1) the sequential model, and (2) the non-sequential model or discrete model.
The most typical sequential representation for a protein sample is its entire amino acid (AA) sequence, which can contain its most complete information. This is an obvious advantage of the sequential model. To get the desired results, the sequence-similarity-search-based tools are usually utilized to conduct the prediction.
Given a protein sequence P with [math]\displaystyle{ L }[/math] amino acid residues, i.e.,
- [math]\displaystyle{ \mathbf{P}={\begin{bmatrix} \mathrm{R}_1 \mathrm{R}_2 \mathrm{R}_3 \mathrm{R}_4 \mathrm{R}_5 \mathrm{R}_6 \mathrm{R}_7 \cdots \mathrm{R}_L\end{bmatrix}} \qquad \text{(1)} }[/math]
where R1 represents the 1st residue of the protein P, R2 the 2nd residue, and so forth. This is the representation of the protein under the sequential model.
However, this kind of approach fails when a query protein does not have significant homology to the known protein(s). Thus, various discrete models were proposed that do not rely on sequence-order. The simplest discrete model is using the amino acid composition (AAC) to represent protein samples. Under the AAC model, the protein P of Eq.1 can also be expressed by
- [math]\displaystyle{ \mathbf{P}={\begin{bmatrix} f_1 & f_2 & \cdots & f_{20} \end{bmatrix}}^{\mathbf{T}} \qquad \text{(2)} }[/math]
where [math]\displaystyle{ \, f_u \, (u=1, 2, \cdots, 20) }[/math] are the normalized occurrence frequencies of the 20 native amino acids in P, and T the transposing operator. The AAC of a protein is trivially derived with the protein primary structure known like given in Eq.1; it is also possible by hydrolysis without knowing the exact sequence, and such a step in fact is often a prerequisite for protein sequencing.[3]
Owing to its simplicity, the amino acid composition (AAC) model was widely used in many earlier statistical methods for predicting protein attributes. However, all the sequence-order information is lost. This is its main shortcoming.
Concept
To avoid completely losing the sequence-order information, the concept of PseAAC (pseudo amino acid composition) was proposed. [1] In contrast with the conventional amino acid composition (AAC) that contains 20 components with each reflecting the occurrence frequency for one of the 20 native amino acids in a protein, the PseAAC contains a set of greater than 20 discrete factors, where the first 20 represent the components of its conventional amino acid composition while the additional factors incorporate some sequence-order information via various pseudo components.
The additional factors are a series of rank-different correlation factors along a protein chain, but they can also be any combinations of other factors so long as they can reflect some sorts of sequence-order effects one way or the other. Therefore, the essence of PseAAC is that on one hand it covers the AA composition, but on the other hand it contains the information beyond the AA composition and hence can better reflect the feature of a protein sequence through a discrete model.
Meanwhile, various modes to formulate the PseAAC vector have also been developed, as summarized in a 2009 review article.[2]
Algorithm
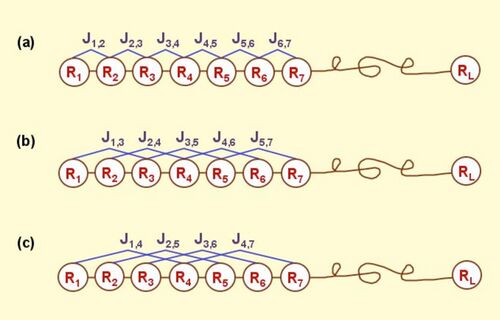
According to the PseAAC model, the protein P of Eq.1 can be formulated as
- [math]\displaystyle{ \mathbf{P}={\begin{bmatrix} p_1, \, p_2, \, \ldots,\, p_{20}, \, p_{20+1}, \, \ldots, \, p_{20+\lambda} \end{bmatrix}}^{\mathbf{T}}, \,\,\, (\lambda \lt L ) \qquad \text{(3)} }[/math]
where the ([math]\displaystyle{ 20+\lambda }[/math]) components are given by
- [math]\displaystyle{ p_u = \begin{cases} \dfrac {f_u} {\sum_{i=1}^{20}f_i \, + \, w\sum_{k=1}^{\lambda} \tau_k}, & (1 \le u \le 20) \\[10pt] \dfrac {w \tau_{u-20}} {\sum_{i=1}^{20} f_i \, + \, w\sum_{k=1}^{\lambda} \tau_k}, & (20+1 \le u \le 20+\lambda) \end{cases} \qquad \text{(4)} }[/math]
where [math]\displaystyle{ w }[/math] is the weight factor, and [math]\displaystyle{ \tau_k }[/math] the [math]\displaystyle{ k }[/math]-th tier correlation factor that reflects the sequence order correlation between all the [math]\displaystyle{ k }[/math]-th most contiguous residues as formulated by
- [math]\displaystyle{ \tau_k = \frac {1}{L-k} \sum_{i=1}^{L-k} \, \mathrm{J}_{i, i+k}, \,\,\, (k \lt L) \qquad \text{(5)} }[/math]
with
- [math]\displaystyle{ \mathrm{J}_{i, i+k} = \frac{1}{\Gamma} \sum_{q=1}^{\Gamma} \left[\Phi_{q}\left(\mathrm{R}_{i+k}\right) - \Phi_{q}\left(\mathrm{R}_{i}\right ) \right]^2 \qquad \text{(6)} }[/math]
where [math]\displaystyle{ \Phi_{q}\left(\mathrm{R}_{i}\right) }[/math] is the [math]\displaystyle{ {q} }[/math]-th function of the amino acid [math]\displaystyle{ \mathrm{R}_i \, }[/math], and [math]\displaystyle{ \Gamma\, }[/math] the total number of the functions considered. For example, in the original paper by Chou,[1] [math]\displaystyle{ \Phi_{1}\left(\mathrm{R}_{i}\right) }[/math], [math]\displaystyle{ \Phi_{2}\left(\mathrm{R}_{i}\right) }[/math] and [math]\displaystyle{ \Phi_{3}\left(\mathrm{R}_{i}\right) }[/math] are respectively the hydrophobicity value, hydrophilicity value, and side chain mass of amino acid [math]\displaystyle{ \mathrm{R}_i \, }[/math]; while [math]\displaystyle{ \Phi_{1}\left(\mathrm{R}_{i+1}\right) }[/math], [math]\displaystyle{ \Phi_{2}\left(\mathrm{R}_{i+1}\right) }[/math] and [math]\displaystyle{ \Phi_{3}\left(\mathrm{R}_{i+1}\right) }[/math] the corresponding values for the amino acid [math]\displaystyle{ \mathrm{R}_{i+1} \, }[/math]. Therefore, the total number of functions considered there is [math]\displaystyle{ \Gamma =3 \, }[/math]. It can be seen from Eq.3 that the first 20 components, i.e. [math]\displaystyle{ p_1, \, p_2, \, \cdots,\, p_{20} }[/math] are associated with the conventional AA composition of protein, while the remaining components [math]\displaystyle{ p_{20+1}, \, \cdots, \, p_{20+\lambda} }[/math] are the correlation factors that reflect the 1st tier, 2nd tier, ..., and the [math]\displaystyle{ \lambda \, }[/math]-th tier sequence order correlation patterns (Figure 1). It is through these additional [math]\displaystyle{ \lambda \, }[/math] factors that some important sequence-order effects are incorporated.
[math]\displaystyle{ \lambda \, }[/math] in Eq.3 is a parameter of integer and that choosing a different integer for [math]\displaystyle{ \lambda \, }[/math] will lead to a dimension-different PseAA composition.[4]
Using Eq.6 is just one of the many modes for deriving the correlation factors in PseAAC or its components. The others, such as the physicochemical distance mode[5] and amphiphilic pattern mode,[6] can also be used to derive different types of PseAAC, as summarized in a 2009 review article.[2] In 2011, the formulation of PseAAC (Eq.3) was extended to a form of the general PseAAC as given by:[7]
- [math]\displaystyle{ \mathbf{P}={\begin{bmatrix} \psi_1, \, \psi_2, \, \ldots,\, \psi_u, \, \ldots, \psi_{\Omega} \end{bmatrix}}^{\mathbf{T}} \,\,\, \qquad \text{(7)} }[/math]
where the subscript [math]\displaystyle{ \Omega }[/math] is an integer, and its value and the components [math]\displaystyle{ \psi_1, \, \psi_2, \, \ldots }[/math] will depend on how to extract the desired information from the amino acid sequence of P in Eq.1.
The general PseAAC can be used to reflect any desired features according to the targets of research, including those core features such as functional domain, sequential evolution, and gene ontology to improve the prediction quality for the subcellular localization of proteins.[8][9] as well as their many other important attributes.
References
- ↑ 1.0 1.1 1.2 "Prediction of protein cellular attributes using pseudo-amino acid composition". Proteins 43 (3): 246–55. May 2001. doi:10.1002/prot.1035. PMID 11288174.
- ↑ 2.0 2.1 2.2 "Pseudo amino acid composition and its applications in bioinformatics, proteomics and system biology.". Current Proteomics 6 (4): 262–274. 2009. doi:10.2174/157016409789973707.
- ↑ Michail A. Alterman; Peter Hunziker (2 December 2011). Amino Acid Analysis: Methods and Protocols. Humana Press. ISBN 978-1-61779-444-5. https://books.google.com/books?id=CLdSXwAACAAJ.
- ↑ "Recent progress in protein subcellular location prediction". Anal. Biochem. 370 (1): 1–16. November 2007. doi:10.1016/j.ab.2007.07.006. PMID 17698024.
- ↑ "Prediction of protein subcellular locations by incorporating quasi-sequence-order effect". Biochem. Biophys. Res. Commun. 278 (2): 477–83. November 2000. doi:10.1006/bbrc.2000.3815. PMID 11097861.
- ↑ "Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes". Bioinformatics 21 (1): 10–9. January 2005. doi:10.1093/bioinformatics/bth466. PMID 15308540.
- ↑ "Some remarks on protein attribute prediction and pseudo amino acid composition". Journal of Theoretical Biology 273 (1): 236–47. March 2011. doi:10.1016/j.jtbi.2010.12.024. PMID 21168420. Bibcode: 2011JThBi.273..236C.
- ↑ "Cell-PLoc: a package of Web servers for predicting subcellular localization of proteins in various organisms". Nat Protoc 3 (2): 153–62. 2008. doi:10.1038/nprot.2007.494. PMID 18274516. http://chou.med.harvard.edu/bioinf/Cell-PLoc/. Retrieved 2008-03-24.
- ↑ "PseAAC: a flexible web server for generating various kinds of protein pseudo amino acid composition". Anal. Biochem. 373 (2): 386–8. February 2008. doi:10.1016/j.ab.2007.10.012. PMID 17976365.
External links
 |

