Prüfer sequence

In combinatorial mathematics, the Prüfer sequence (also Prüfer code or Prüfer numbers) of a labeled tree is a unique sequence associated with the tree. The sequence for a tree on n vertices has length n − 2, and can be generated by a simple iterative algorithm. Prüfer sequences were first used by Heinz Prüfer to prove Cayley's formula in 1918.

Algorithm to convert a tree into a Prüfer sequence

One can generate a labeled tree's Prüfer sequence by iteratively removing vertices from the tree until only two vertices remain. Specifically, consider a labeled tree T with vertices {1, 2, ..., n}. At step i, remove the leaf with the smallest label and set the ith element of the Prüfer sequence to be the label of this leaf's neighbour.

The Prüfer sequence of a labeled tree is unique and has length n − 2.

Both coding and decoding can be reduced to integer radix sorting and parallelized.

Example

A labeled tree with Prüfer sequence {4,4,4,5}.

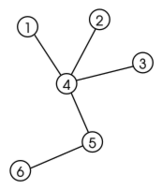
Consider the above algorithm run on the tree shown to the right. Initially, vertex 1 is the leaf with the smallest label, so it is removed first and 4 is put in the Prüfer sequence. Vertices 2 and 3 are removed next, so 4 is added twice more. Vertex 4 is now a leaf and has the smallest label, so it is removed and we append 5 to the sequence. We are left with only two vertices, so we stop. The tree's sequence is {4,4,4,5}.

Algorithm to convert a Prüfer sequence into a tree

Let {a[1], a[2], ..., a[n]} be a Prüfer sequence:

The tree will have n+2 nodes, numbered from 1 to n+2. For each node set its degree to the number of times it appears in the sequence plus 1. For instance, in pseudo-code:

 Convert-Prüfer-to-Tree(a)
 1 n ← length[a]
 2 T ← a graph with n + 2 isolated nodes, numbered 1 to n + 2
 3 degree ← an array of integers
 4 for each node i in T do
 5     degree[i] ← 1
 6 for each value i in a do
 7     degree[i] ← degree[i] + 1

Next, for each number in the sequence a[i], find the first (lowest-numbered) node, j, with degree equal to 1, add the edge (j, a[i]) to the tree, and decrement the degrees of j and a[i]. In pseudo-code:

 8 for each value i in a do
 9     for each node j in T do
10         if degree[j] = 1 then
11             Insert edge[i, j] into T
12             degree[i] ← degree[i] - 1
13             degree[j] ← degree[j] - 1
14             break

At the end of this loop two nodes with degree 1 will remain (call them u, v). Lastly, add the edge (u,v) to the tree.

15 u ← v ← 0
16 for each node i in T
17     if degree[i] = 1 then
18         if u = 0 then
19             u ← i
20         else
21             v ← i
22             break
23 Insert edge[u, v] into T
24 degree[u] ← degree[u] - 1
25 degree[v] ← degree[v] - 1
26 return T

Cayley's formula

The Prüfer sequence of a labeled tree on n vertices is a unique sequence of length n − 2 on the labels 1 to n. For a given sequence S of length n − 2 on the labels 1 to n, there is a unique labeled tree whose Prüfer sequence is S.

The immediate consequence is that Prüfer sequences provide a bijection between the set of labeled trees on n vertices and the set of sequences of length n − 2 on the labels 1 to n. The latter set has size nⁿ⁻², so the existence of this bijection proves Cayley's formula, i.e. that there are nⁿ⁻² labeled trees on n vertices.

Other applications

• Cayley's formula can be strengthened to prove the following claim:

The number of spanning trees in a complete graph [math]\displaystyle{ K_n }[/math] with a degree [math]\displaystyle{ d_i }[/math] specified for each vertex [math]\displaystyle{ i }[/math] is equal to the multinomial coefficient

[math]\displaystyle{ \binom{n-2}{d_1-1,\,d_2-1,\,\dots,\,d_n-1}=\frac{(n-2)!}{(d_1-1)!(d_2-1)!\cdots(d_{n}-1)!}. }[/math]

The proof follows by observing that in the Prüfer sequence number [math]\displaystyle{ i }[/math] appears exactly [math]\displaystyle{ d_i-1 }[/math] times.

• Cayley's formula can be generalized: a labeled tree is in fact a spanning tree of the labeled complete graph. By placing restrictions on the enumerated Prüfer sequences, similar methods can give the number of spanning trees of a complete bipartite graph. If G is the complete bipartite graph with vertices 1 to n₁ in one partition and vertices n₁ + 1 to n in the other partition, the number of labeled spanning trees of G is [math]\displaystyle{ n_1^{n_2-1} n_2^{n_1-1} }[/math], where n₂ = n − n₁.
• Generating uniformly distributed random Prüfer sequences and converting them into the corresponding trees is a straightforward method of generating uniformly distributed random labelled trees.

External links

• Prüfer code – from MathWorld