Wagner's theorem

Short description: On forbidden minors in planar graphs

K₅ (left) and K_3,3 (right) as minors of the nonplanar Petersen graph (small colored circles and solid black edges). The minors may be formed by deleting the red vertex and contracting edges within each yellow circle.

A clique-sum of two planar graphs and the Wagner graph, forming a K₅-free graph.

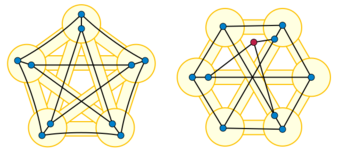
In graph theory, Wagner's theorem is a mathematical forbidden graph characterization of planar graphs, named after Klaus Wagner, stating that a finite graph is planar if and only if its minors include neither K₅ (the complete graph on five vertices) nor K_3,3 (the utility graph, a complete bipartite graph on six vertices). This was one of the earliest results in the theory of graph minors and can be seen as a forerunner of the Robertson–Seymour theorem.

Definitions and statement

A planar embedding of a given graph is a drawing of the graph in the Euclidean plane, with points for its vertices and curves for its edges, in such a way that the only intersections between pairs of edges are at a common endpoint of the two edges. A minor of a given graph is another graph formed by deleting vertices, deleting edges, and contracting edges. When an edge is contracted, its two endpoints are merged to form a single vertex. In some versions of graph minor theory the graph resulting from a contraction is simplified by removing self-loops and multiple adjacencies, while in other version multigraphs are allowed, but this variation makes no difference to Wagner's theorem. Wagner's theorem states that every graph has either a planar embedding, or a minor of one of two types, the complete graph K₅ or the complete bipartite graph K_3,3. (It is also possible for a single graph to have both types of minor.)

If a given graph is planar, so are all its minors: vertex and edge deletion obviously preserve planarity, and edge contraction can also be done in a planarity-preserving way, by leaving one of the two endpoints of the contracted edge in place and routing all of the edges that were incident to the other endpoint along the path of the contracted edge. A minor-minimal non-planar graph is a graph that is not planar, but in which all proper minors (minors formed by at least one deletion or contraction) are planar. Another way of stating Wagner's theorem is that there are only two minor-minimal non-planar graphs, K₅ and K_3,3.

Another result also sometimes known as Wagner's theorem states that a four-connected graph is planar if and only if it has no K₅ minor. That is, by assuming a higher level of connectivity, the graph K_3,3 can be made unnecessary in the characterization, leaving only a single forbidden minor, K₅. Correspondingly, the Kelmans–Seymour conjecture states that a 5-connected graph is planar if and only if it does not have K₅ as a topological minor.

History and relation to Kuratowski's theorem

Wagner published both theorems in 1937, subsequent to the 1930 publication of Kuratowski's theorem, according to which a graph is planar if and only if it does not contain as a subgraph a subdivision of one of the same two forbidden graphs K₅ and K_3,3. In a sense, Kuratowski's theorem is stronger than Wagner's theorem: a subdivision can be converted into a minor of the same type by contracting all but one edge in each path formed by the subdivision process, but converting a minor into a subdivision of the same type is not always possible. However, in the case of the two graphs K₅ and K_3,3, it is straightforward to prove that a graph that has at least one of these two graphs as a minor also has at least one of them as a subdivision, so the two theorems are equivalent.

Implications

One consequence of the stronger version of Wagner's theorem for four-connected graphs is to characterize the graphs that do not have a K₅ minor. The theorem can be rephrased as stating that every such graph is either planar or it can be decomposed into simpler pieces. Using this idea, the K₅-minor-free graphs may be characterized as the graphs that can be formed as combinations of planar graphs and the eight-vertex Wagner graph, glued together by clique-sum operations. For instance, K_3,3 can be formed in this way as a clique-sum of three planar graphs, each of which is a copy of the tetrahedral graph K₄.

Wagner's theorem is an important precursor to the theory of graph minors, which culminated in the proofs of two deep and far-reaching results: the graph structure theorem (a generalization of Wagner's clique-sum decomposition of K₅-minor-free graphs) and the Robertson–Seymour theorem (a generalization of the forbidden minor characterization of planar graphs, stating that every graph family closed under the operation of taking minors has a characterization by a finite number of forbidden minors). Analogues of Wagner's theorem can also be extended to the theory of matroids: in particular, the same two graphs K₅ and K_3,3 (along with three other forbidden configurations) appear in a characterization of the graphic matroids by forbidden matroid minors.