Matroid
In combinatorics, a matroid /ˈmeɪtrɔɪd/ is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.
Matroid theory borrows extensively from the terms used in both linear algebra and graph theory, largely because it is the abstraction of various notions of central importance in these fields. Matroids have found applications in geometry, topology, combinatorial optimization, network theory, and coding theory.[1][2]
Definition
There are many equivalent ways to define a (finite) matroid.[lower-alpha 1]

Independent sets
In terms of independence, a finite matroid is a pair , where is a finite set (called the ground set) and is a family of subsets of (called the independent sets) with the following properties:[4]
- (I1) The empty set is independent, i.e., .
- (I2) Every subset of an independent set is independent, i.e., for each , if then . This is sometimes called the hereditary property, or the downward-closed property.
- (I3) If and are two independent sets (i.e., each set is independent) and has more elements than , then there exists such that is in . This is sometimes called the augmentation property or the independent set exchange property.
The first two properties define a combinatorial structure known as an independence system (or abstract simplicial complex). Actually, assuming (I2), property (I1) is equivalent to the fact that at least one subset of is independent, i.e., .
Bases and circuits
A subset of the ground set that is not independent is called dependent. A maximal independent set – that is, an independent set that becomes dependent upon adding any element of – is called a basis for the matroid. A circuit in a matroid is a minimal dependent subset of – that is, a dependent set whose proper subsets are all independent. The term arises because the circuits of graphic matroids are cycles in the corresponding graphs.[4]
The dependent sets, the bases, or the circuits of a matroid characterize the matroid completely: a set is independent if and only if it is not dependent, if and only if it is a subset of a basis, and if and only if it does not contain a circuit. The collections of dependent sets, of bases, and of circuits each have simple properties that may be taken as axioms for a matroid. For instance, one may define a matroid to be a pair , where is a finite set as before and is a collection of subsets of , called bases, with the following properties:[4]
- (B1) is nonempty.
- (B2) If and are distinct members of and , then there exists an element such that .
This property (B2) is called the basis exchange property. It follows from this property that no member of can be a proper subset of any other.
Rank functions
It is a basic result of matroid theory, directly analogous to a similar theorem of bases in linear algebra, that any two bases of a matroid have the same number of elements. This number is called the rank of . If is a matroid on , and is a subset of , then a matroid on can be defined by considering a subset of to be independent if and only if it is independent in . This allows us to talk about submatroids and about the rank of any subset of . The rank of a subset is given by the rank function of the matroid, which has the following properties:[4]
- (R1) The value of the rank function is always a non-negative integer.
- (R2) For any subset , we have .
- (R3) For any two subsets , we have: . That is, the rank is a submodular function.
- (R4) For any set and element , we have: . From the first inequality it follows more generally that, if , then . That is, rank is a monotonic function.
These properties can be used as one of the alternative definitions of a finite matroid: If satisfies these properties, then the independent sets of a matroid over can be defined as those subsets of with . In the language of partially ordered sets, such a matroid structure is equivalent to the geometric lattice whose elements are the subsets , partially ordered by inclusion.
The difference is called the nullity of the subset . It is the minimum number of elements that must be removed from to obtain an independent set. The nullity of in is called the nullity of . The difference is sometimes called the corank of the subset .
Closure operators
Let be a matroid on a finite set , with rank function as above. The closure or span of a subset of is the set
- .
This defines a closure operator where denotes the power set, with the following properties:
- (C1) For all subsets of , .
- (C2) For all subsets of , .
- (C3) For all subsets and of with , .
- (C4) For all elements and from and all subsets of , if then .
The first three of these properties are the defining properties of a closure operator. The fourth is sometimes called the Mac Lane–Steinitz exchange property. These properties may be taken as another definition of matroid: every function that obeys these properties determines a matroid.[4]
Flats
A set whose closure equals itself is said to be closed, or a flat or subspace of the matroid.[5] A set is closed if it is maximal for its rank, meaning that the addition of any other element to the set would increase the rank. The closed sets of a matroid are characterized by a covering partition property:
- (F1) The whole point set is closed.
- (F2) If and are flats, then is a flat.
- (F3) If is a flat, then each element of is in precisely one of the flats that cover (meaning that properly contains , but there is no flat between and ).
The class of all flats, partially ordered by set inclusion, forms a matroid lattice. Conversely, every matroid lattice forms a matroid over its set of atoms under the following closure operator: for a set of atoms with join ,
- .
The flats of this matroid correspond one-for-one with the elements of the lattice; the flat corresponding to lattice element is the set
- .
Thus, the lattice of flats of this matroid is naturally isomorphic to .
Hyperplanes
In a matroid of rank , a flat of rank is called a hyperplane. (Hyperplanes are also called co-atoms or copoints.) These are the maximal proper flats; that is, the only superset of a hyperplane that is also a flat is the set of all the elements of the matroid. An equivalent definition is that a coatom is a subset of E that does not span M, but such that adding any other element to it does make a spanning set.[6]
The family of hyperplanes of a matroid has the following properties, which may be taken as yet another axiomatization of matroids:[6]
- (H1) The ground set itself is not a hyperplane.
- (H2) There do not exist distinct sets and in with . That is, the hyperplanes form a Sperner family.
- (H3) For every and distinct with , there exists with .
Graphoids
Minty (1966) defined a graphoid as a triple in which and are classes of nonempty subsets of such that
- (G1) no element of (called a "circuit") contains another,
- (G2) no element of (called a "cocircuit") contains another,
- (G3) no set in and set in intersect in exactly one element, and
- (G4) whenever is represented as the disjoint union of subsets with (a singleton set), then either an exists such that or a exists such that .
He proved that there is a matroid for which is the class of circuits and is the class of cocircuits. Conversely, if and are the circuit and cocircuit classes of a matroid with ground set , then is a graphoid. Thus, graphoids give a self-dual cryptomorphic axiomatization of matroids.
Examples
Free matroid
Let be a finite set. The set of all subsets of defines the independent sets of a matroid. It is called the free matroid over .
Uniform matroids
Let be a finite set and a natural number. One may define a matroid on by taking every element subset of to be a basis. This is known as the uniform matroid of rank . A uniform matroid with rank and with elements is denoted . All uniform matroids of rank at least 2 are simple (see § Additional terms). The uniform matroid of rank 2 on points is called the point line. A matroid is uniform if and only if it has no circuits of size less than one plus the rank of the matroid. The direct sums of uniform matroids are called partition matroids.
In the uniform matroid , every element is a loop (an element that does not belong to any independent set), and in the uniform matroid , every element is a coloop (an element that belongs to all bases). The direct sum of matroids of these two types is a partition matroid in which every element is a loop or a coloop; it is called a discrete matroid. An equivalent definition of a discrete matroid is a matroid in which every proper, non-empty subset of the ground set is a separator.
Matroids from linear algebra
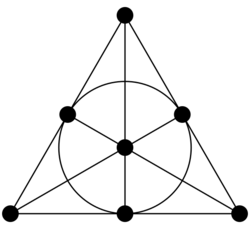
Matroid theory developed mainly out of a deep examination of the properties of independence and dimension in vector spaces. There are two ways to present the matroids defined in this way:
- If is any finite subset of a vector space , then we can define a matroid on by taking the independent sets of to be the linearly independent subsets of .
The validity of the independent set axioms for this matroid follows from the Steinitz exchange lemma.
- If is a matroid that can be defined in this way, we say the set represents .
- Matroids of this kind are called vector matroids.
An important example of a matroid defined in this way is the Fano matroid, a rank three matroid derived from the Fano plane, a finite geometry with seven points (the seven elements of the matroid) and seven lines (the proper nontrivial flats of the matroid). It is a linear matroid whose elements may be described as the seven nonzero points in a three dimensional vector space over the finite field GF(2). However, it is not possible to provide a similar representation for the Fano matroid using the real numbers in place of GF(2).
A matrix with entries in a field gives rise to a matroid on its set of columns. The dependent sets of columns in the matroid are those that are linearly dependent as vectors.
- This matroid is called the column matroid of , and is said to represent .
For instance, the Fano matroid can be represented in this way as a 3 × 7 (0,1) matrix. Column matroids are just vector matroids under another name, but there are often reasons to favor the matrix representation.[lower-alpha 2]
A matroid that is equivalent to a vector matroid, although it may be presented differently, is called representable or linear. If is equivalent to a vector matroid over a field , then we say is representable over ; in particular, is real representable if it is representable over the real numbers. For instance, although a graphic matroid (see below) is presented in terms of a graph, it is also representable by vectors over any field.
A basic problem in matroid theory is to characterize the matroids that may be represented over a given field ; Rota's conjecture describes a possible characterization for every finite field. The main results so far are characterizations of binary matroids (those representable over GF(2)) due to Tutte (1950s), of ternary matroids (representable over the 3 element field) due to Reid and Bixby, and separately to Seymour (1970s), and of quaternary matroids (representable over the 4 element field) due to Geelen, Gerards & Kapoor (2000). A proof of Rota's conjecture was announced, but not published, in 2014 by Geelen, Gerards, and Whittle.[7]
A regular matroid is a matroid that is representable over all possible fields. The Vámos matroid is the simplest example of a matroid that is not representable over any field.
Matroids from graph theory
A second original source for the theory of matroids is graph theory.
Every finite graph (or multigraph) gives rise to a matroid as follows: take as the set of all edges in and consider a set of edges independent if and only if it is a forest; that is, if it does not contain a simple cycle. Then is called a cycle matroid. Matroids derived in this way are graphic matroids. Not every matroid is graphic, but all matroids on three elements are graphic.[8] Every graphic matroid is regular.
Other matroids on graphs were discovered subsequently:
- The bicircular matroid of a graph is defined by calling a set of edges independent if every connected subset contains at most one cycle ie a set of edges is independent if and only if it is a pseudoforest .
- In any directed or undirected graph let and be two distinguished sets of vertices. In the set , define a subset to be independent if there are vertex-disjoint paths from onto . This defines a matroid on called a gammoid:[9] a strict gammoid is one for which the set is the whole vertex set of .[10]
- In a bipartite graph , one may form a matroid in which the elements are vertices on one side of the bipartition, and the independent subsets are sets of endpoints of matchings of the graph. This is called a transversal matroid,[11][12] and it is a special case of a gammoid.[9] The transversal matroids are the dual matroids to the strict gammoids.[10]
- Graphic matroids have been generalized to matroids from signed graphs, gain graphs, and biased graphs. A graph with a distinguished linear class of cycles, known as a "biased graph" , has two matroids, known as the frame matroid and the lift matroid of the biased graph.
- If every cycle belongs to the distinguished class, these matroids coincide with the cycle matroid of . If no cycle is distinguished, the frame matroid is the bicircular matroid of . A signed graph, whose edges are labeled by signs, and a gain graph, which is a graph whose edges are labeled orientably from a group, each give rise to a biased graph and therefore have frame and lift matroids.
- The Laman graphs form the bases of the two dimensional rigidity matroid, a matroid defined in the theory of structural rigidity.
- Let be a connected graph and be its edge set. Let be the collection of subsets of such that is still connected. Then , whose element set is and with as its class of independent sets, is a matroid called the bond matroid of .
- The rank function is the cyclomatic number of the subgraph induced on the edge subset , which equals the number of edges outside a maximal forest of that subgraph, and also the number of independent cycles in it.
Matroids from field extensions
A third original source of matroid theory is field theory.
An extension of a field gives rise to a matroid:
- Suppose and are fields with containing . Let be any finite subset of .
- Define a subset of to be algebraically independent if the extension field has transcendence degree equal to .[13]
A matroid that is equivalent to a matroid of this kind is called an algebraic matroid.[14] The problem of characterizing algebraic matroids is extremely difficult; little is known about it. The Vámos matroid provides an example of a matroid that is not algebraic.
Basic constructions
There are some standard ways to make new matroids out of old ones.
Duality
If is a finite matroid, we can define the orthogonal or dual matroid by taking the same underlying set and calling a set a basis in if and only if its complement is a basis in . It is not difficult to verify that is a matroid and that the dual of is .[15]
The dual can be described equally well in terms of other ways to define a matroid. For instance:
- A set is independent in if and only if its complement spans .
- A set is a circuit of if and only if its complement is a coatom in .
- The rank function of the dual is .
According to a matroid version of Kuratowski's theorem, the dual of a graphic matroid is a graphic matroid if and only if is the matroid of a planar graph. In this case, the dual of is the matroid of the dual graph of .[16] The dual of a vector matroid representable over a particular field is also representable over . The dual of a transversal matroid is a strict gammoid and vice versa.
- Example
- The cycle matroid of a graph is the dual matroid of its bond matroid.
Minors
If M is a matroid with element set E, and S is a subset of E, the restriction of M to S, written M |S, is the matroid on the set S whose independent sets are the independent sets of M that are contained in S. Its circuits are the circuits of M that are contained in S and its rank function is that of M restricted to subsets of S.
In linear algebra, this corresponds to restricting to the subspace generated by the vectors in S. Equivalently if T = M−S this may be termed the deletion of T, written M\T or M−T. The submatroids of M are precisely the results of a sequence of deletions: the order is irrelevant.[17][18]
The dual operation of restriction is contraction.[19] If T is a subset of E, the contraction of M by T, written M/T, is the matroid on the underlying set E − T whose rank function is .[20] In linear algebra, this corresponds to looking at the quotient space by the linear space generated by the vectors in T, together with the images of the vectors in E - T.
A matroid N that is obtained from M by a sequence of restriction and contraction operations is called a minor of M.[18][21] We say M contains N as a minor. Many important families of matroids may be characterized by the minor-minimal matroids that do not belong to the family; these are called forbidden or excluded minors.[22]
Sums and unions
Let M be a matroid with an underlying set of elements E, and let N be another matroid on an underlying set F. The direct sum of matroids M and N is the matroid whose underlying set is the disjoint union of E and F, and whose independent sets are the disjoint unions of an independent set of M with an independent set of N.
The union of M and N is the matroid whose underlying set is the union (not the disjoint union) of E and F, and whose independent sets are those subsets that are the union of an independent set in M and one in N. Usually the term "union" is applied when E = F, but that assumption is not essential. If E and F are disjoint, the union is the direct sum.
Additional terms
Let M be a matroid with an underlying set of elements E.
- E may be called the ground set of M. Its elements may be called the points of M.
- A subset of E spans M if its closure is E. A set is said to span a closed set K if its closure is K.
- The girth of a matroid is the size of its smallest circuit or dependent set.
- An element that forms a single-element circuit of M is called a loop. Equivalently, an element is a loop if it belongs to no basis.[8][23]
- An element that belongs to no circuit is called a coloop or isthmus. Equivalently, an element is a coloop if it belongs to every basis.
- Loop and coloops are mutually dual.[23]
- If a two-element set {f, g} is a circuit of M, then f and g are parallel in M.[8]
- A matroid is called simple if it has no circuits consisting of 1 or 2 elements. That is, it has no loops and no parallel elements. The term combinatorial geometry is also used.[8] A simple matroid obtained from another matroid M by deleting all loops and deleting one element from each 2-element circuit until no 2 element circuits remain is called a simplification of M.[24] A matroid is co-simple if its dual matroid is simple.[25]
- A union of circuits is sometimes called a cycle of M. A cycle is therefore the complement of a flat of the dual matroid. (This usage conflicts with the common meaning of "cycle" in graph theory.)
- A separator of M is a subset S of E such that . A proper or non-trivial separator is a separator that is neither E nor the empty set.[26] An irreducible separator is a non-empty separator that contains no other non-empty separator. The irreducible separators partition the ground set E.
- A matroid that cannot be written as the direct sum of two nonempty matroids, or equivalently that has no proper separators, is called connected or irreducible. A matroid is connected if and only if its dual is connected.[27]
- A maximal irreducible submatroid of M is called a component of M. A component is the restriction of M to an irreducible separator, and contrariwise, the restriction of M to an irreducible separator is a component. A separator is a union of components.[26]
- A matroid M is called a frame matroid if it, or a matroid that contains it, has a basis such that all the points of M are contained in the lines that join pairs of basis elements.[28]
- A matroid is called a paving matroid if all of its circuits have size at least equal to its rank.[29]
- The basis polytope is the convex hull of the indicator vectors of the bases of
- The independence polytope of is the convex hull of the indicator vectors of the independent sets of .
Algorithms
Several important combinatorial optimization problems can be solved efficiently on every matroid. In particular:
- Finding a maximum-weight independent set in a weighted matroid can be solved by a greedy algorithm. This fact may even be used to characterize matroids: if a family F of sets, closed under taking subsets, has the property that, no matter how the sets are weighted, the greedy algorithm finds a maximum-weight set in the family, then F must be the family of independent sets of a matroid.[30]
- The matroid partitioning problem is to partition the elements of a matroid into as few independent sets as possible, and the matroid packing problem is to find as many disjoint spanning sets as possible. Both can be solved in polynomial time, and can be generalized to the problem of computing the rank or finding an independent set in a matroid sum.
- A matroid intersection of two or more matroids on the same ground set is the family of sets that are simultaneously independent in each of the matroids. The problem of finding the largest set, or the maximum weighted set, in the intersection of two matroids can be found in polynomial time, and provides a solution to many other important combinatorial optimization problems. For instance, maximum matching in bipartite graphs can be expressed as a problem of intersecting two partition matroids. However, finding the largest set in an intersection of three or more matroids is NP-complete.
Matroid software
Two standalone systems for calculations with matroids are Kingan's Oid and Hlineny's Macek. Both of them are open-sourced packages. "Oid" is an interactive, extensible software system for experimenting with matroids. "Macek" is a specialized software system with tools and routines for reasonably efficient combinatorial computations with representable matroids.
Both open source mathematics software systems SAGE and Macaulay2 contain matroid packages. Maple has a package for dealing with matroids since the version 2024.[31]
Polynomial invariants
There are two especially significant polynomials associated to a finite matroid M on the ground set E. Each is a matroid invariant, which means that isomorphic matroids have the same polynomial.
Characteristic polynomial
The characteristic polynomial of M – sometimes called the chromatic polynomial,[32] although it does not count colorings – is defined to be
or equivalently (as long as the empty set is closed in M) as
- ,
where μ denotes the Möbius function of the geometric lattice of the matroid and the sum is taken over all the flats A of the matroid.[33]
- When M is the cycle matroid M(G) of a graph G, the characteristic polynomial is a slight transformation of the chromatic polynomial, which is given by χG (λ) = λcpM(G) (λ), where c is the number of connected components of G.
- When M is the bond matroid M*(G) of a graph G, the characteristic polynomial equals the flow polynomial of G.
- When M is the matroid M(A) of an arrangement A of linear hyperplanes in (or Fn where F is any field), the characteristic polynomial of the arrangement is given by pA (λ) = λn−r(M)pM (λ).
Beta invariant
The beta invariant of a matroid, introduced by Crapo (1967), may be expressed in terms of the characteristic polynomial as an evaluation of the derivative[34]
or directly as[35]
- .
The beta invariant is non-negative, and is zero if and only if is disconnected, or empty, or a loop. Otherwise it depends only on the lattice of flats of . If has no loops and coloops then .[35]
Whitney numbers
The Whitney numbers of the first kind of are the coefficients of the powers of in the characteristic polynomial. Specifically, the th Whitney number is the coefficient of and is the sum of Möbius function values:
summed over flats of the right rank. These numbers alternate in sign, so that for .
The Whitney numbers of the second kind of are the numbers of flats of each rank. That is, is the number of rank flats.
The Whitney numbers of both kinds generalize the Stirling numbers of the first and second kind, which are the Whitney numbers of the cycle matroid of the complete graph, and equivalently of the partition lattice. They were named after Hassler Whitney, the (co)founder of matroid theory, by Gian-Carlo Rota. The name has been extended to the similar numbers for finite ranked partially ordered sets.
Tutte polynomial
The Tutte polynomial of a matroid, , generalizes the characteristic polynomial to two variables. This gives it more combinatorial interpretations, and also gives it the duality property
- ,
which implies a number of dualities between properties of and properties of . One definition of the Tutte polynomial is
- .
This expresses the Tutte polynomial as an evaluation of the co-rank-nullity or rank generating polynomial,[36]
- .
From this definition it is easy to see that the characteristic polynomial is, up to a simple factor, an evaluation of , specifically,
- .
Another definition is in terms of internal and external activities and a sum over bases, reflecting the fact that is the number of bases.[37] This, which sums over fewer subsets but has more complicated terms, was Tutte's original definition.
There is a further definition in terms of recursion by deletion and contraction.[38] The deletion-contraction identity is
when is neither a loop nor a coloop. An invariant of matroids (i.e., a function that takes the same value on isomorphic matroids) satisfying this recursion and the multiplicative condition
is said to be a Tutte-Grothendieck invariant.[36] The Tutte polynomial is the most general such invariant; that is, the Tutte polynomial is a Tutte-Grothendieck invariant and every such invariant is an evaluation of the Tutte polynomial.[32]
The Tutte polynomial of a graph is the Tutte polynomial of its cycle matroid.
Infinite matroids
The theory of infinite matroids is much more complicated than that of finite matroids and forms a subject of its own. For a long time, one of the difficulties has been that there were many reasonable and useful definitions, none of which appeared to capture all the important aspects of finite matroid theory. For instance, it seemed to be hard to have bases, circuits, and duality together in one notion of infinite matroids.
The simplest definition of an infinite matroid is to require finite rank; that is, the rank of E is finite. This theory is similar to that of finite matroids except for the failure of duality due to the fact that the dual of an infinite matroid of finite rank does not have finite rank. Finite-rank matroids include any subsets of finite-dimensional vector spaces and of field extensions of finite transcendence degree.
The next simplest infinite generalization is finitary matroids, also known as pregeometries. A matroid with possibly infinite ground set is finitary if it has the property that
Equivalently, every dependent set contains a finite dependent set.
Examples are linear dependence of arbitrary subsets of infinite-dimensional vector spaces (but not infinite dependencies as in Hilbert and Banach spaces), and algebraic dependence in arbitrary subsets of field extensions of possibly infinite transcendence degree. Again, the class of finitary matroid is not self-dual, because the dual of a finitary matroid is not finitary.
Finitary infinite matroids are studied in model theory, a branch of mathematical logic with strong ties to algebra.
In the late 1960s matroid theorists asked for a more general notion that shares the different aspects of finite matroids and generalizes their duality. Many notions of infinite matroids were defined in response to this challenge, but the question remained open. One of the approaches examined by D.A. Higgs became known as B-matroids and was studied by Higgs, Oxley, and others in the 1960s and 1970s. According to a recent result by Bruhn et al. (2013), it solves the problem: Arriving at the same notion independently, they provided five equivalent systems of axiom—in terms of independence, bases, circuits, closure and rank. The duality of B-matroids generalizes dualities that can be observed in infinite graphs.
The independence axioms are as follows:
- The empty set is independent.
- Every subset of an independent set is independent.
- For every nonmaximal (under set inclusion) independent set and maximal independent set , there is such that is independent.
- For every subset of the base space, every independent subset of can be extended to a maximal independent subset of .
With these axioms, every matroid has a dual.
History
Matroid theory was introduced by Whitney (1935). It was also independently discovered by Takeo Nakasawa, whose work was forgotten for many years (Nishimura & Kuroda (2009)).
In his seminal paper, Whitney provided two axioms for independence, and defined any structure adhering to these axioms to be "matroids".[lower-alpha 3] His key observation was that these axioms provide an abstraction of "independence" that is common to both graphs and matrices. Because of this, many of the terms used in matroid theory resemble the terms for their analogous concepts in linear algebra or graph theory.
Almost immediately after Whitney first wrote about matroids, an important article was written by MacLane (1936) on the relation of matroids to projective geometry. A year later, van der Waerden (1937) noted similarities between algebraic and linear dependence in his classic textbook on Modern Algebra.
In the 1940s Richard Rado developed further theory under the name "independence systems" with an eye towards transversal theory, where his name for the subject is still sometimes used.
In the 1950s W.T. Tutte became the foremost figure in matroid theory, a position he retained for many years. His contributions were plentiful, including
- the characterization of binary, regular, and graphic matroids by excluded minors
- the regular-matroid representability theorem
- the theory of chain groups and their matroids
and the tools he used to prove many of his results:
- the "Path theorem"
- "Tutte homotopy theorem" (see, e.g., Tutte (1965))
which are so complicated that later theorists have gone to great trouble to eliminate the need for them in proofs.[lower-alpha 4]
Crapo (1969) and Brylawski (1972) generalized to matroids Tutte's "dichromate", a graphic polynomial now known as the Tutte polynomial (named by Crapo). Their work has recently (especially in the 2000s) been followed by a flood of papers—though not as many as on the Tutte polynomial of a graph.
In 1976 Dominic Welsh published the first comprehensive book on matroid theory.
Paul Seymour's decomposition theorem for regular matroids (Seymour (1980)) was the most significant and influential work of the late 1970s and the 1980s. Another fundamental contribution, by Kahn & Kung (1982), showed why projective geometries and Dowling geometries play such an important role in matroid theory.
By the 1980s there were many other important contributors, but one should not omit to mention Geoff Whittle's extension to ternary matroids of Tutte's characterization of binary matroids that are representable over the rationals (Whittle 1995), perhaps the biggest single contribution of the 1990s.
In the current period (since around 2000) the Matroid Minors Project of Geelen, Gerards, Whittle, and others,[lower-alpha 5] has produced substantial advances in the structure theory of matroids. Many others have also contributed to that part of matroid theory, which (in the first and second decades of the 21st century) is flourishing.
Researchers
Mathematicians who pioneered the study of matroids include
- Susumu Kuroda[39]
- Saunders MacLane
- Richard Rado
- Takeo Nakasawa
- Hirokazu Nishimura[39]
- William T. Tutte
- Bartel L. van der Waerden
- Hassler Whitney
Some of the other major contributors are
- Jack Edmonds
- Jim Geelen
- Eugene Lawler
- László Lovász
- Gian-Carlo Rota
- Paul D. Seymour
- Dominic Welsh
Footnotes
- ↑
Oxley (1992) is a standard source for basic definitions and results about matroids; Welsh (1976) is an older standard source.
- ↑ There is one technical difference: A column matroid can have distinct elements that are the same vector, but a vector matroid as defined above cannot. Usually this difference is insignificant and can be ignored, but by letting be a multiset of vectors one brings the two definitions into complete agreement.
- ↑
Although it was perhaps implied, Whitney (1935) did not include an axiom requiring at least one subset to be independent.
- ↑ A fine example is A.M.H. Gerards' short proof (Gerards (1989)) of Tutte's characterization of regular matroids.
- ↑ The Matroid Minors Project is an attempt to duplicate, for matroids that are representable over a finite field, the success of the Robertson–Seymour Graph Minors Project (see Robertson–Seymour theorem).
See also
- Antimatroid – Mathematical system of orderings or sets with antiexchange axiom
- Coxeter matroid – Group-theoretic generalization of matroids
- Greedoid
- Oriented matroid – Abstraction of ordered linear algebra
- Polymatroid
- Pregeometry (model theory) – Formulation of matroids using closure operators
Citations
- ↑ Neel & Neudauer (2009)
- ↑ Kashyap, Soljanin & Vontobel (2009)
- ↑ Welsh, D. J. A. (2010). Matroid Theory. Courier Dover Publications. p. 10. ISBN 9780486474397.
- ↑ 4.0 4.1 4.2 4.3 4.4 (Welsh 1976), Section 1.2, "Axiom Systems for a Matroid".
- ↑ (Welsh 1976), Section 1.8, "Closed sets = Flats = Subspaces".
- ↑ 6.0 6.1 (Welsh 1976), Section 2.2, "The Hyperplanes of a Matroid".
- ↑ "Solving Rota's conjecture". Notices of the American Mathematical Society: 736–743. Aug 17, 2014. http://www.ams.org/notices/201407/rnoti-p736.pdf.
- ↑ 8.0 8.1 8.2 8.3 Oxley (1992), p. 13
- ↑ 9.0 9.1 Oxley (1992), pp. 115
- ↑ 10.0 10.1 Oxley (1992), p. 100
- ↑ Oxley (1992), pp. 46–48
- ↑ White (1987), pp. 72–97
- ↑ Oxley (1992), p. 215
- ↑ Oxley (1992), p. 216
- ↑ White (1986), p. 32
- ↑ White (1986), p. 105
- ↑ White (1986), p. 131
- ↑ 18.0 18.1 White (1986), p. 224
- ↑ White (1986), p. 139
- ↑ White (1986), p. 140
- ↑ White (1986), p. 150
- ↑ White (1986), pp. 146–147
- ↑ 23.0 23.1 White (1986), p. 130
- ↑ Oxley (1992), p. 52
- ↑ Oxley (1992), p. 347
- ↑ 26.0 26.1 Oxley (1992), p. 128
- ↑ White (1986), p. 110
- ↑ Zaslavsky (1994)
- ↑ Oxley (1992), p. 26
- ↑ Oxley (1992), p. 64
- ↑ "The Matroids and Hypergraphs Packages in Maple 2024". MapleSoft. https://www.maplesoft.com/products/maple/new_features/Maple2024/PDFs/Maple2024-MatroidsHypergraphs.pdf.
- ↑ 32.0 32.1 White (1987), p. 127
- ↑ White (1987), p. 120
- ↑ White (1987), p. 123
- ↑ 35.0 35.1 White (1987), p. 124
- ↑ 36.0 36.1 White (1987), p. 126
- ↑ White (1992b), p. 188
- ↑ White (1986), p. 260
- ↑ 39.0 39.1 Nishimura & Kuroda (2009)
References
- Bruhn, Henning; Diestel, Reinhard; Kriesell, Matthias; Pendavingh, Rudi; Wollan, Paul (2013). "Axioms for infinite matroids". Advances in Mathematics 239: 18–46. doi:10.1016/j.aim.2013.01.011.
- Bryant, Victor (1980). Independence Theory in Combinatorics. London, UK & New York, NY: Chapman and Hall. ISBN 978-0-412-22430-0.
- "A decomposition for combinatorial geometries". Transactions of the American Mathematical Society 171: 235–282. 1972. doi:10.2307/1996381.
- "The Tutte polynomial". Aequationes Mathematicae 3 (3): 211–229. 1969. doi:10.1007/BF01817442.
- On the Foundations of Combinatorial Theory: Combinatorial geometries. Cambridge, MA: M.I.T. Press. 1970. ISBN 978-0-262-53016-3. https://archive.org/details/onfoundationsofc00crap.
- Jünger, Michael; Reinelt, Gerhard; Rinaldi, Giovanni, eds (5–9 March 2001). "Submodular functions, matroids, and certain polyhedra". 5th International Workshop. 2570 (revised papers ed.). Aussois, FR: Berlin, Heidelberg: Springer (published 2003). pp. 11–26. doi:10.1007/3-540-36478-1_2. ISBN 978-3-540-36478-8.
- Geelen, J. F.; Gerards, A. M. H.; Kapoor, A. (2000). "The excluded minors for GF(4)-representable matroids". Journal of Combinatorial Theory. Series B 79 (2): 247–299. doi:10.1006/jctb.2000.1963.
- "Towards a matroid-minor structure theory". Combinatorics, Complexity, and Chance: A tribute to Dominic Welsh. Oxford Lecture Series in Mathematics and its Applications. 34. Oxford, UK: Oxford University Press. 2007. pp. 72–82.
- Gerards, A.M.H. (1989). "A short proof of Tutte's characterization of totally unimodular matrices". Linear Algebra and Its Applications 114-115: 207–212. doi:10.1016/0024-3795(89)90461-8.
- Kahn, Jeff; Kung, Joseph P.S. (1982). "Varieties of combinatorial geometries". Transactions of the American Mathematical Society 271 (2): 485–499. doi:10.2307/1998894.
- Kingan, Robert; Kingan, Sandra (2005). "A software system for matroids". Graphs and Discovery. DIMACS Series in Discrete Mathematics and Theoretical Computer Science. pp. 287–296.
- Kashyap, Navin; Soljanin, Emina; Vontobel, Pascal (2009). Applications of matroid theory and combinatorial optimization to information and coding theory (Report). https://www.birs.ca/workshops/2009/09w5103/report09w5103.pdf. Retrieved 4 October 2014.
- Kung, Joseph P.S., ed (1986). A Source Book in Matroid Theory. Boston, MA: Birkhäuser. doi:10.1007/978-1-4684-9199-9. ISBN 978-0-8176-3173-4. https://archive.org/details/sourcebookinmatr0000kung.
- "Some interpretations of abstract linear dependence in terms of projective geometry". American Journal of Mathematics 58 (1): 236–240. 1936. doi:10.2307/2371070.
- Minty, George J. (1966). "On the axiomatic foundations of the theories of directed linear graphs, electrical networks and network-programming". Journal of Mathematics and Mechanics 15: 485–520.
- Neel, David L. (2009). "Matroids you have known". Mathematics Magazine 82 (1): 26–41. doi:10.4169/193009809x469020. http://www.maa.org/sites/default/files/pdf/shortcourse/2011/matroidsknown.pdf. Retrieved 4 October 2014.
- Nishimura, Hirokazu; Kuroda, Susumu, eds (2009). A lost mathematician, Takeo Nakasawa: The forgotten father of matroid theory. Basel, CH: Birkhäuser Verlag. doi:10.1007/978-3-7643-8573-6. ISBN 978-3-7643-8572-9.
- Matroid Theory. Oxford, UK: Oxford University Press. 1992. ISBN 978-0-19-853563-8.
- Recski, András (1989). Matroid Theory and its Applications in Electric Network Theory and in Statics. Algorithms and Combinatorics. 6. Berlin, DE & Budapest, HU: Springer-Verlag and Akademiai Kiado. doi:10.1007/978-3-662-22143-3. ISBN 978-3-540-15285-9. https://archive.org/details/matroidtheoryits0000recs.
- Hazewinkel, Michiel, ed. (2001), "M/m062870", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=M/m062870
- "Decomposition of regular matroids". Journal of Combinatorial Theory. Series B 28 (3): 305–359. 1980. doi:10.1016/0095-8956(80)90075-1.
- Truemper, Klaus (1992). Matroid Decomposition. Boston, MA: Academic Press. ISBN 978-0-12-701225-4. http://www.emis.de/monographs/md/index.html.
- "Matroids and graphs". Transactions of the American Mathematical Society 90 (3): 527–552. 1959. doi:10.2307/1993185.
- "Lectures on matroids". Journal of Research of the National Bureau of Standards. Section B 69: 1–47. 1965.
- Introduction to the Theory of Matroids. Modern Analytic and Computational Methods in Science and Mathematics. 37. New York, NY: American Elsevier Publishing Company. 1971.
- Vámos, Peter (1978). "The missing axiom of matroid theory is lost forever". Journal of the London Mathematical Society 18 (3): 403–408. doi:10.1112/jlms/s2-18.3.403.
- Moderne Algebra. 1937.
- Welsh, D.J.A. (1976). Matroid Theory. L.M.S. Monographs. 8. Academic Press. ISBN 978-0-12-744050-7.
- White, Neil, ed (1986). Theory of Matroids. Encyclopedia of Mathematics and its Applications. 26. Cambridge, UK: Cambridge University Press. ISBN 978-0-521-30937-0. https://archive.org/details/theoryofmatroids1986unse.
- White, Neil, ed (1987). Combinatorial Geometries. Encyclopedia of Mathematics and its Applications. 29. Cambridge, UK: Cambridge University Press. ISBN 978-0-521-33339-9. https://archive.org/details/combinatorialgeo0000unse.
- White, Neil, ed (1992a). Matroid Applications. Encyclopedia of Mathematics and its Applications. 40. Cambridge, UK: Cambridge University Press. ISBN 978-0-521-38165-9. https://archive.org/details/matroidapplicati0000unse.
- "On the abstract properties of linear dependence". American Journal of Mathematics 57 (3): 509–533. 1935. doi:10.2307/2371182. — Reprinted in Kung (1986), pp. 55–79
- Whittle, Geoff (1995). "A characterization of the matroids representable over GF(3) and the rationals". Journal of Combinatorial Theory. Series B 65 (2): 222–261. doi:10.1006/jctb.1995.1052.
- Zaslavsky, Thomas (1994). "Frame matroids and biased graphs". Eur. J. Comb. 15 (3): 303–307. doi:10.1006/eujc.1994.1034. ISSN 0195-6698.
External links
- Hazewinkel, Michiel, ed. (2001), "Matroid", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page
- Kingan, Sandra. "Matroid theory". City University of New York. http://userhome.brooklyn.cuny.edu/skingan/matroids/. — A large bibliography of matroid papers, matroid software, and links.
- Locke, S.C.. "Greedy algorithms". Florida Atlantic University. http://euler.math.fau.edu/locke/Greedy.htm.
- Pagano, Steven R.. "Matroids and signed graphs". Binghamton University. http://www.math.binghamton.edu/zaslav/Pagano/Matridx.htm.
- Hubenthal, Mark. "A brief look at matroids". University of Washington. http://www.math.washington.edu/~hubenjm/matroid2.pdf. — Gives proofs for statements in this article.
- Oxley, James. "What is a matroid?". Louisiana State University. https://www.math.lsu.edu/~oxley/survey4.pdf.
- White, Neil, ed (1992b). Matroid Applications. Cambridge University Press. ISBN 978-0-5213-8165-9. https://books.google.com/books?id=uD2H-RAcBpwC&dq=greedoid+theory&pg=PP1.
 |
