Physics:Anderson's bridge

Short description: Circuit in electronics

Anderson's bridge

In electronics, Anderson's bridge is a bridge circuit used to measure the self-inductance of the coil. It enables measurement of inductance by utilizing other circuit components like resistors and capacitors.

Anderson's bridge was invented by Alexander Anderson in 1891. He modified Maxwell's inductance capacitance bridge so that it gives very accurate measurement of self-inductance.

Balance conditions

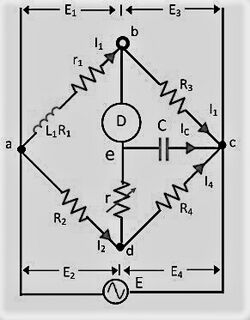
The balance conditions for Anderson's bridge or, equivalently the values of the self-inductance and resistance of the given coil can be found using basic circuit analysis techniques such as KCL, KVL and using phasors. Consider the circuit diagram of Anderson's bridge in the given figure. Let L₁ be the self-inductance and R₁ be the electrical resistance of the coil under consideration. Since the voltmeter is ideally assumed to have nearly infinite impedance, the currents in branches ab and bc and those in the branches de and ec are taken to be equal. Applying Kirchhoff's current law at node d, it can be shown that-

[math]\displaystyle{ \begin{align} I_4 + I_c &= I_2 \end{align} }[/math]

Since the analysis is being made under the balanced condition of the bridge, it can be said that the voltage drop across the voltmeter is essentially zero. On applying Kirchhoff's voltage law to the appropriate loops(in the anti-clockwise direction), the following relations hold-

[math]\displaystyle{ \begin{align} I_1(R_1 + r_1 + j \omega L_1) - I_2 R_2 - I_c r = 0 \\ I_1 R_3 - \frac{I_c}{j \omega C} = 0 \\ I_c r + \frac{I_c}{j \omega C} - I_4 R_4 = 0 \end{align} }[/math]

On solving these sets of equations, one can finally obtain the self-inductance and resistance of the coil as-

[math]\displaystyle{ \begin{align} L_1 &= (\frac{R_3}{R_4})(R_2 R_4 + r(R_2 + R_4))C \\ R_1 &= \frac{R_2 R_3}{R_4} - r_1 \end{align} }[/math]

Advantages

The Anderson's bridge can also be used the other way round- that is, it can be used to measure the capacitance of an unknown capacitor using an inductor coil whose self-inductance and electrical resistance have been pre-determined to a high degree of precision. An interesting point to note is the fact that the measured self-inductance of the coil does not change even on taking dielectric loss within the capacitor into account. Another advantage of using this modified bridge is that unlike the variable capacitor used in Maxwell bridge, it makes use of a fixed capacitor which is relatively quite cheaper.

Disadvantages

One of the obvious difficulties associated with Anderson's bridge are the relatively complex balance equation calculations compared to the Maxwell bridge. The circuit connections and computations are similarly more cumbersome in comparison to the Maxwell bridge.