Physics:X-ray magnetic circular dichroism
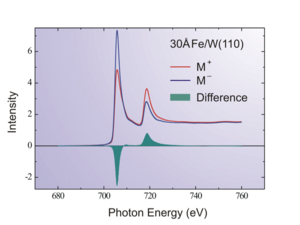
X-ray magnetic circular dichroism (XMCD) is a difference spectrum of two X-ray absorption spectra (XAS) taken in a magnetic field, one taken with left circularly polarized light, and one with right circularly polarized light.[1] By closely analyzing the difference in the XMCD spectrum, information can be obtained on the magnetic properties of the atom, such as its spin and orbital magnetic moment. Using XMCD magnetic moments below 10−5 µB can be observed.[2]
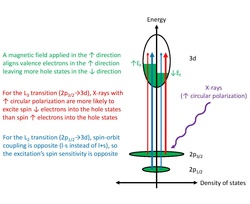
In the case of transition metals such as iron, cobalt, and nickel, the absorption spectra for XMCD are usually measured at the L-edge. This corresponds to the process in the iron case: with iron, a 2p electron is excited to a 3d state by an X-ray of about 700 eV.[3] Because the 3d electron states are the origin of the magnetic properties of the elements, the spectra contain information on the magnetic properties. In rare-earth elements usually, the M4,5-edges are measured, corresponding to electron excitations from a 3d state to mostly 4f states.
Line intensities and selection rules
The line intensities and selection rules of XMCD can be understood by considering the transition matrix elements of an atomic state [math]\displaystyle{ \vert{njm}\rangle }[/math] excited by circularly polarised light.[4][5] Here [math]\displaystyle{ n }[/math] is the principal, [math]\displaystyle{ j }[/math] the angular momentum and [math]\displaystyle{ m }[/math] the magnetic quantum numbers. The polarisation vector of left and right circular polarised light can be rewritten in terms of spherical harmonics[math]\displaystyle{ \mathbf{e} = \frac{1}{\sqrt{2}}\left(x \pm iy\right) = \sqrt{\frac{4\pi}{3}} r Y^{\pm 1}_{1}\left(\theta,\varphi\right) }[/math]leading to an expression for the transition matrix element [math]\displaystyle{ \langle n^{\prime}j^{\prime}m^{\prime}\vert \mathbf{e}\cdot\mathbf{r}\vert njm\rangle }[/math] which can be simplified using the 3-j symbol:[math]\displaystyle{ \langle n^{\prime}j^{\prime}m^{\prime}\vert \mathbf{e}\cdot\mathbf{r}\vert njm\rangle = \sqrt{\frac{4\pi}{3}}\langle n^{\prime}j^{\prime}m^{\prime}\vert rY_{1}^{\pm 1}\left(\theta,\varphi\right)\vert njm\rangle\propto \int_{0}^{\infty}dr~rR_{n^{\prime}j^{\prime}}(r)R_{nj}(r)\int_{\Omega}d\Omega~{Y_{j^{\prime}}^{m^{\prime}}}^{*}\left(\theta,\varphi\right) Y_{1}^{\pm 1}\left(\theta,\varphi\right) Y_{ j}^{m}\left(\theta,\varphi\right) = \sqrt{\frac{(2j^{\prime}+1) (2j+1)}{4 \pi}} \langle{j^{\prime}~0~j~0}\vert {1~0}\rangle \langle {j^{\prime} ~ m^{\prime}~j~m}\vert {1 ~ \pm 1}\rangle }[/math]The radial part is referred to as the line strength while the angular one contains symmetries from which selection rules can be deduced. Rewriting the product of three spherical harmonics with the 3-j symbol finally leads to[4]:[math]\displaystyle{ \sqrt{\frac{(2j^{\prime}+1)(2j+1)}{4 \pi}} \langle {j^{\prime}~0~j~0}\vert {1~0}\rangle \langle {j^{\prime} ~ m^{\prime}~j~m}\vert {1 ~ \pm 1}\rangle = \sqrt{\frac{(2j^{\prime} + 1)(2j + 1)(2 + 1)}{4\pi}} \begin{pmatrix} {j^{\prime}} & j & 1 \\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} j^{\prime} & j & 1 \\ m^{\prime} & m & \mp 1\end{pmatrix} }[/math]The 3-j symbols are not zero only if [math]\displaystyle{ j, j^{\prime},m,m^{\prime} }[/math] satisfy the following conditions giving us the following selection rules for dipole transitions with circular polarised light:[4]
- [math]\displaystyle{ \Delta J = \pm 1 }[/math]
- [math]\displaystyle{ \Delta m = 0, \pm 1 }[/math]
See also
References
- ↑ Zhao, Jijun; Huang, Xiaoming; Jin, Peng; Chen, Zhongfang (April 2015). "Magnetic properties of atomic clusters and endohedral metallofullerenes" (in en). Coordination Chemistry Reviews 289-290: 315–340. doi:10.1016/j.ccr.2014.12.013. ISSN 0010-8545. https://www.sciencedirect.com/topics/chemistry/x-ray-magnetic-circular-dichroism.
- ↑ Handbook of magnetism and advanced magnetic materials. Helmut Kronmüller, Stuart S. P. Parkin. Hoboken, NJ: John Wiley & Sons. 2007. ISBN 978-0-470-02217-7. OCLC 124165851. https://www.worldcat.org/oclc/124165851.
- ↑ Stöhr, J. (1995-12-15). "X-ray magnetic circular dichroism spectroscopy of transition metal thin films" (in en). Journal of Electron Spectroscopy and Related Phenomena. Future Perspectives for Electron Spectroscopy with Synchrotron Radiation 75: 253–272. doi:10.1016/0368-2048(95)02537-5. ISSN 0368-2048. https://dx.doi.org/10.1016/0368-2048%2895%2902537-5.
- ↑ 4.0 4.1 4.2 de Groot, F. and Vogel, J. (2006). "Fundamentals of X-ray Absorption and Dichroism: The Multiplet Approach" in "Neutron and X-ray Spectroscopy". pp. 3-66. doi:10.1007/1-4020-3337-0_1. ISBN 978-1-4020-3337-7.
- ↑ J. Stöhr and Y. Wu (1994). "X-ray Magnetic Circular Dichroism: Basic concepts and theory for 3d transition metal atoms" in "New Directions in Research with Third-Generation Soft X-Ray Synchrotron Radiation Sources". pp. 221-250. doi:10.1007/978-94-011-0868-3. ISBN 978-94-010-4375-5.
 |