Physics:Ballistic conduction

Short description: Movement of charge carriers with negligible scattering

In mesoscopic physics, ballistic conduction (ballistic transport) is the unimpeded flow (or transport) of charge carriers (usually electrons), or energy-carrying particles, over relatively long distances in a material. In general, the resistivity of a material exists because an electron, while moving inside a medium, is scattered by impurities, defects, thermal fluctuations of ions in a crystalline solid, or, generally, by any freely-moving atom/molecule composing a gas or liquid. Without scattering, electrons simply obey Newton's second law of motion at non-relativistic speeds.

The mean free path of a particle can be described as the average length that the particle can travel freely, i.e., before a collision, which could change its momentum. The mean free path can be increased by reducing the number of impurities in a crystal or by lowering its temperature. Ballistic transport is observed when the mean free path of the particle is (much) longer than the dimension of the medium through which the particle travels. The particle alters its motion only upon collision with the walls. In the case of a wire suspended in air/vacuum the surface of the wire plays the role of the box reflecting the electrons and preventing them from exiting toward the empty space/open air. This is because there is an energy to be paid to extract the electron from the medium (work function).

Ballistic conduction is typically observed in quasi-1D structures, such as carbon nanotubes or silicon nanowires, because of extreme size quantization effects in these materials. Ballistic conduction is not limited to electrons (or holes) but can also apply to phonons. It is theoretically possible for ballistic conduction to be extended to other quasi-particles, but this has not been experimentally verified. For a specific example, ballistic transport can be observed in a metal nanowire: due to the small size of the wire (nanometer-scale or 10⁻⁹ meters scale) and the mean free path which can be longer than that in a metal.

Ballistic conduction differs from superconductivity due to the absence of the Meissner effect in the material. A ballistic conductor would stop conducting if the driving force is turned off, whereas in a superconductor current would continue to flow after the driving supply is disconnected.

Theory

Scattering mechanisms

In general, carriers will exhibit ballistic conduction when [math]\displaystyle{ L \le \lambda_{\rm MFP} }[/math] where [math]\displaystyle{ L }[/math] is the length of the active part of the device (e.g., a channel in a MOSFET). [math]\displaystyle{ \lambda_{\rm MFP} }[/math] is the mean free path for the carrier which can be given by Matthiessen's rule, written here for electrons:

[math]\displaystyle{ \frac{1}{\lambda_\mathrm{MFP}} = \frac{1}{\lambda_\mathrm{el-el}} + \frac{1}{\lambda_\mathrm{ap}} + \frac{1}{\lambda_\mathrm{op,ems}} + \frac{1}{\lambda_\mathrm{op,abs}} + \frac{1}{\lambda_\mathrm{impurity}} + \frac{1}{\lambda_\mathrm{defect}} + \frac{1}{\lambda_\mathrm{boundary}} }[/math]

where

• [math]\displaystyle{ \lambda_\mathrm{el-el} }[/math] is the electron-electron scattering length,
• [math]\displaystyle{ \lambda_\mathrm{ap} }[/math] is the acoustic phonon (emission and absorption) scattering length,
• [math]\displaystyle{ \lambda_\mathrm{op,ems} }[/math] is the optical phonon emission scattering length,
• [math]\displaystyle{ \lambda_\mathrm{op,abs} }[/math] is the optical phonon absorption scattering length,
• [math]\displaystyle{ \lambda_\mathrm{impurity} }[/math] is the electron-impurity scattering length,
• [math]\displaystyle{ \lambda_\mathrm{defect} }[/math] is the electron-defect scattering length,
• and [math]\displaystyle{ \lambda_\mathrm{boundary} }[/math] is the electron scattering length with the boundary.

In terms of scattering mechanisms, optical phonon emission normally dominates, depending on the material and transport conditions. There are also other scattering mechanisms which apply to different carriers that are not considered here (e.g. remote interface phonon scattering, Umklapp scattering). To get these characteristic scattering rates, one would need to derive a Hamiltonian and solve Fermi's golden rule for the system in question.

A graphene nanoribbon field-effect transistor (GNR-FET). Here contacts A and B are at two different Fermi levels [math]\displaystyle{ E_{\rm F_A} }[/math] and [math]\displaystyle{ E_{\rm F_B} }[/math].

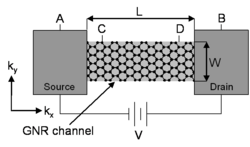
Landauer–Büttiker formalism

In 1957, Rolf Landauer proposed that conduction in a 1D system could be viewed as a transmission problem. For the 1D graphene nanoribbon field effect transistor (GNR-FET) on the right (where the channel is assumed to be ballistic), the current from A to B, given by the Boltzmann transport equation, is

[math]\displaystyle{ I_{\rm AB} = \frac{g_\text{s}e}{h}\int_{E_{\rm F_B}}^{E_{\rm F_{ A}}}M(E)f^{\prime}(E)T(E)dE }[/math],

where g_s = 2, due to spin degeneracy, e is the electron charge, h is the Planck constant, [math]\displaystyle{ E_{\rm F_A} }[/math] and [math]\displaystyle{ E_{\rm F_B} }[/math] are the Fermi levels of A and B, M(E) is the number of propagating modes in the channel, f′(E) is the deviation from the equilibrium electron distribution (perturbation), and T(E) is the transmission probability (T = 1 for ballistic). Based on the definition of conductance

[math]\displaystyle{ G = \frac{I}{V} }[/math],

and the voltage separation between the Fermi levels is approximately [math]\displaystyle{ eV = E_{\rm F_A}-E_{\rm F_B} }[/math], it follows that

[math]\displaystyle{ G = G_0MT }[/math], with [math]\displaystyle{ G_0=\frac{2e^2}{h} }[/math]

where M is the number of modes in the transmission channel and spin is included. [math]\displaystyle{ G_0 }[/math] is known as the conductance quantum. The contacts have a multiplicity of modes due to their larger size in comparison to the channel. Conversely, the quantum confinement in the 1D GNR channel constricts the number of modes to carrier degeneracy and restrictions from the energy dispersion relationship and the Brillouin zone. For example, electrons in carbon nanotubes have two intervalley modes and two spin modes. Since the contacts and the GNR channel are connected by leads, the transmission probability is smaller at contacts A and B,

[math]\displaystyle{ T\approx\frac{M}{M_{\rm contact}} }[/math].

Thus the quantum conductance is approximately the same if measured at A and B or C and D.

The Landauer–Büttiker formalism holds as long as the carriers are coherent (which means the length of the active channel is less than the phase-breaking mean free path) and the transmission functions can be calculated from Schrödinger's equation or approximated by semiclassical approximations, like the WKB approximation. Therefore, even in the case of a perfect ballistic transport, there is a fundamental ballistic conductance which saturates the current of the device with a resistance of approximately 12.9 kΩ per mode (spin degeneracy included). There is, however, a generalization of the Landauer–Büttiker formalism of transport applicable to time-dependent problems in the presence of dissipation.

Importance

Ballistic conduction enables use of quantum mechanical properties of electron wave functions. Ballistic transport is coherent in wave mechanics terms. Phenomena like double-slit interference, spatial resonance (and other optical or microwave-like effects) could be exploited in electronic systems at nanoscale in systems including nanowires and nanotubes.

The widely encountered phenomenon of electrical contact resistance or ECR, arises as an electric current flowing through a rough interface is restricted to a limited number of contact spots. The size and distribution of these contact spots is governed by the topological structures of the contacting surfaces forming the electrical contact. In particular, for surfaces with high fractal dimension contact spots may be very small. In such cases, when the radius of the contact spot is smaller than the mean free path of electrons [math]\displaystyle{ \lambda }[/math] , the resistance is dominated by the Sharvin mechanism, in which electrons travel ballistically through these micro-contacts with resistance that can be described by the following

[math]\displaystyle{ R_{\rm S} = \frac{\lambda(\rho_1+\rho_2)}{2a}. }[/math]

This term, where [math]\displaystyle{ \rho_1 }[/math] and [math]\displaystyle{ \rho_2 }[/math] correspond to the specific resistivity of the two contacting surfaces, is known as Sharvin resistance. Electrical contacts resulting in ballistic electron conduction are known as Sharvin Contacts. When the radius of a contact spot is larger than the mean free path of electrons, the contact resistance can be treated classically.

Optical analogies

A comparison with light provides an analogy between ballistic and non-ballistic conduction. Ballistic electrons behave like light in a waveguide or a high-quality optical assembly. Non-ballistic electrons behave like light diffused in milk or reflected off a white wall or a piece of paper.

Electrons can be scattered several ways in a conductor. Electrons have several properties: wavelength (energy), direction, phase, and spin orientation. Different materials have different scattering probabilities which cause different incoherence rates (stochasticity). Some kinds of scattering can only cause a change in electron direction, others can cause energy loss.

Consider a coherent source of electrons connected to a conductor. Over a limited distance, the electron wave function will remain coherent. You still can deterministically predict its behavior (and use it for computation theoretically). After some greater distance, scattering causes each electron to have a slightly different phase and/or direction. But there is still almost no energy loss. Like monochromatic light passing through milk, electrons undergo elastic interactions. Information about the state of the electrons at the input is then lost. Transport becomes statistical and stochastic. From the resistance point of view, stochastic (not oriented) movement of electrons is useless even if they carry the same energy – they move thermally. If the electrons undergo inelastic interactions too, they lose energy and the result is a second mechanism of resistance. Electrons which undergo inelastic interaction are then similar to non-monochromatic light.

For correct usage of this analogy consideration of several facts is needed:

1. photons are bosons and electrons are fermions;
2. there is coulombic repulsion between electrons thus this analogy is good only for single-electron conduction because electron processes are strongly nonlinear and dependent on other electrons;
3. it is more likely that an electron would lose more energy than a photon would, because of the electron's non-zero rest mass;
4. electron interactions with the environment, each other, and other particles are generally stronger than interactions with and between photons.

Examples

As mentioned, nanostructures such as carbon nanotubes or graphene nanoribbons are often considered ballistic, but these devices only very closely resemble ballistic conduction. Their ballisticity is nearly 0.9 at room temperature.

Carbon nanotubes and graphene nanoribbon

The dominant scattering mechanism at room temperature is that of electrons emitting optical phonons. If electrons don't scatter with enough phonons (for example if the scattering rate is low), the mean free path tends to be very long ([math]\displaystyle{ \lambda_{MFP} \approx 1{\mu} }[/math]m). So a nanotube or graphene nanoribbon could be a good ballistic conductor if the electrons in transit don't scatter with too many phonons and if the device is about 100 nm long. Such a transport regime has been found to depend on the nanoribbon edge structure and the electron energy.

Silicon nanowires

It is often incorrectly thought that Si nanowires are quantum confined ballistic conductors. There are major differences between carbon nanotubes (which are hollow) and Si nanowires (which are solid). Nanowires are about 20–50 nm in diameter and are 3D solid while carbon nanotubes have diameters around the wavelength of the electrons (2–3 nm) and are essentially 1D conductors. However it is still possible to observe ballistic conduction in Si nanowires at very low temperatures (2–3 K).

Isotopically enriched diamond

Isotopically pure diamond can have a significantly higher thermal conductivity. See List of thermal conductivities.

See also

• Engineering:Adiabatic circuit – Low-power electronic circuits which use reversible logic to conserve energy
• Engineering:Ballistic collection transistor
• Engineering:Ballistic deflection transistor
• Physics:Velocity overshoot

Further reading

• Du, Xu; Skachko, Ivan; Barker, Anthony; Andrei, Eva Y. (2008-07-20). "Approaching ballistic transport in suspended graphene" (in En). Nature Nanotechnology 3 (8): 491–495. doi:10.1038/nnano.2008.199. ISSN 1748-3387. PMID 18685637. Bibcode: 2008NatNa...3..491D. 
• Jalabert, R. A.; Pichard, J.-L.; Beenakker, C. W. J. (1994). "Universal Quantum Signatures of Chaos in Ballistic Transport" (in en). EPL (Europhysics Letters) 27 (4): 255. doi:10.1209/0295-5075/27/4/001. ISSN 0295-5075. Bibcode: 1994EL.....27..255J.