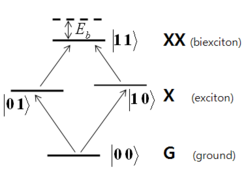Physics:Biexciton
In condensed matter physics, biexcitons are created from two free excitons.
Formation of biexcitons
In quantum information and computation, it is essential to construct coherent combinations of quantum states. The basic quantum operations can be performed on a sequence of pairs of physically distinguishable quantum bits and, therefore, can be illustrated by a simple four-level system.
In an optically driven system where the [math]\displaystyle{ | 0 1 \rangle }[/math] and [math]\displaystyle{ | 1 0 \rangle }[/math] states can be directly excited, direct excitation of the upper [math]\displaystyle{ | 1 1 \rangle }[/math] level from the ground state [math]\displaystyle{ | 0 0 \rangle }[/math] is usually forbidden and the most efficient alternative is coherent nondegenerate two-photon excitation, using [math]\displaystyle{ | 0 1 \rangle }[/math] or [math]\displaystyle{ | 1 0 \rangle }[/math] as an intermediate state.[1][2]
Observation of biexcitons
Three possibilities of observing biexcitons exist:[3]
(a) excitation from the one-exciton band to the biexciton band (pump-probe experiments);
(b) two-photon absorption of light from the ground state to the biexciton state;
(c) luminescence from a biexciton state made up from two free excitons in a dense exciton system.
Binding energy of biexcitons
The biexciton is a quasi-particle formed from two excitons, and its energy is expressed as
- [math]\displaystyle{ E_{XX} = 2 E_{X} - E_{b} }[/math]
where [math]\displaystyle{ E_{XX} }[/math] is the biexciton energy, [math]\displaystyle{ E_{X} }[/math] is the exciton energy, and [math]\displaystyle{ E_{b} }[/math] is the biexciton binding energy.
When a biexciton is annihilated, it disintegrates into a free exciton and a photon. The energy of the photon is smaller than that of the exciton by the biexciton binding energy, so the biexciton luminescence peak appears on the low-energy side of the exciton peak.
The biexciton binding energy in semiconductor quantum dots has been the subject of extensive theoretical study. Because a biexciton is a composite of two electrons and two holes, we must solve a four-body problem under spatially restricted conditions. The biexciton binding energies for CuCl quantum dots, as measured by the site selective luminescence method, increased with decreasing quantum dot size. The data were well fitted by the function
- [math]\displaystyle{ B_{XX} = \frac{c_1}{a^2} + \frac{c_2}{a} + B_{bulk} }[/math]
where [math]\displaystyle{ B_{XX} }[/math] is biexciton binding energy, [math]\displaystyle{ a }[/math] is the radius of the quantum dots, [math]\displaystyle{ B_{bulk} }[/math] is the binding energy of bulk crystal, and [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math] are fitting parameters.[4]
A simple model for describing binding energy of biexcitons
In the effective-mass approximation, the Hamiltonian of the system consisting of two electrons (1, 2) and two holes (a, b) is given by
- [math]\displaystyle{ H_{XX} = - \frac{\hbar^2}{2 m_e^*} ({\nabla_1}^2 + {\nabla_2}^2) - \frac{\hbar^2}{2 m_h^*} ({\nabla_a}^2 + {\nabla_b}^2) + V }[/math]
where [math]\displaystyle{ m_e^* }[/math] and [math]\displaystyle{ m_h^* }[/math] are the effective masses of electrons and holes, respectively, and
- [math]\displaystyle{ V = V_{12} - V_{1a} - V_{1b} - V_{2a} - V_{2b} + V_{ab} }[/math]
where [math]\displaystyle{ V_{ij} }[/math] denotes the Coulomb interaction between the charged particles [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] ([math]\displaystyle{ i, j = 1, 2, a, b }[/math] denote the two electrons and two holes in the biexciton) given by
- [math]\displaystyle{ V_{ij} = \frac{e^2}{\epsilon |\mathbf{r}_i - \mathbf{r}_j|} }[/math]
where [math]\displaystyle{ \epsilon }[/math] is the dielectric constant of the material.
Denoting [math]\displaystyle{ \mathbf{R} }[/math] and [math]\displaystyle{ \mathbf{r} }[/math] are the c.m. coordinate and the relative coordinate of the biexciton, respectively, and [math]\displaystyle{ M = m_e^* + m_h^* }[/math] is the effective mass of the exciton, the Hamiltonian becomes
- [math]\displaystyle{ H_{XX} = - \frac{\hbar^2}{4 M} {\nabla_R}^2 - \frac{\hbar^2}{M} {\nabla_r}^2 - \frac{\hbar^2}{2 \mu} ({\nabla_{1a}}^2 + {\nabla_{2b}}^2) + V }[/math]
where [math]\displaystyle{ 1/\mu = 1/{m_e^*} + 1/{m_h^*} }[/math]; [math]\displaystyle{ {\nabla_{1a}}^2 }[/math] and [math]\displaystyle{ {\nabla_{2b}}^2 }[/math] are the Laplacians with respect to relative coordinates between electron and hole, respectively. And [math]\displaystyle{ {\nabla_r}^2 }[/math] is that with respect to relative coordinate between the c. m. of excitons, and [math]\displaystyle{ {\nabla_R}^2 }[/math] is that with respect to the c. m. coordinate [math]\displaystyle{ \mathbf{R} }[/math] of the system.
In the units of the exciton Rydberg and Bohr radius, the Hamiltonian can be written in dimensionless form
- [math]\displaystyle{ H_{XX} = - ({\nabla_{1a}}^2 + {\nabla_{2b}}^2) - {2 \sigma}{(1 + \sigma)^2} {\nabla_r}^2 + V }[/math]
where [math]\displaystyle{ \sigma = {m_e^*}/{m_h^*} }[/math] with neglecting kinetic energy operator of c. m. motion. And [math]\displaystyle{ V }[/math] can be written as
- [math]\displaystyle{ V = 2 \left(\frac{1}{r_{12}} - \frac{1}{r_{1a}} - \frac{1}{r_{1b}} - \frac{1}{r_{2a}} - \frac{1}{r_{2b}} + \frac{1}{r_{ab}}\right) }[/math]
To solve the problem of the bound states of the biexciton complex, it is required to find the wave functions [math]\displaystyle{ \psi }[/math] satisfying the wave equation
- [math]\displaystyle{ H_{XX} \psi = E_{XX} \psi }[/math]
If the eigenvalue [math]\displaystyle{ E_{XX} }[/math] can be obtained, the binding energy of the biexciton can be also acquired
- [math]\displaystyle{ E_{b} = 2 E_{X} - E_{XX} }[/math]
where [math]\displaystyle{ {E_{b}} }[/math] is the binding energy of the biexciton and [math]\displaystyle{ {E_{X}} }[/math] is the energy of exciton.[5]
Numerical calculations of the binding energies of biexcitons
The diffusion Monte Carlo (DMC) method provides a straightforward means of calculating the binding energies of biexcitons within the effective mass approximation. For a biexciton composed of four distinguishable particles (e.g., a spin-up electron, a spin-down electron, a spin-up hole and a spin-down hole), the ground-state wave function is nodeless and hence the DMC method is exact. DMC calculations have been used to calculate the binding energies of biexcitons in which the charge carriers interact via the Coulomb interaction in two and three dimensions,[6] indirect biexcitons in coupled quantum wells,[7][8] and biexcitons in monolayer transition metal dichalcogenide semiconductors.[9][10][11]
Binding energy in nanotubes
Biexcitons with bound complexes formed by two excitons are predicted to be surprisingly stable for carbon nanotube in a wide diameter range. Thus, a biexciton binding energy exceeding the inhomogeneous exciton line width is predicted for a wide range of nanotubes.
The biexciton binding energy in carbon nanotube is quite accurately approximated by an inverse dependence on [math]\displaystyle{ r }[/math], except perhaps for the smallest values of [math]\displaystyle{ r }[/math].
- [math]\displaystyle{ E_{XX} \approx \frac{0.195 eV}{r} }[/math]
The actual biexciton binding energy is inversely proportional to the physical nanotube radius.[12] Experimental evidence of biexcitons in carbon nanotubes was found in 2012. [13]
Binding energy in CuCl QDs
The binding energy of biexcitons increase with the decrease in their size and its size dependence and bulk value are well represented by the expression
- [math]\displaystyle{ \frac{78}{{a^*}^2} + \frac{52}{{a^*}} + 33 }[/math] (meV)
where [math]\displaystyle{ a^* }[/math] is the effective radius of microcrystallites in a unit of nm. The enhanced Coulomb interaction in microcrystallites still increase the biexciton binding energy in the large-size regime, where the quantum confinement energy of excitons is not considerable.[14]
References
- ↑ Chen, Gang; Stievater, T. H.; Batteh, E. T.; Li, Xiaoqin; Steel, D. G.; Gammon, D.; Katzer, D. S.; Park, D. et al. (2002). "Biexciton Quantum Coherence in a Single Quantum Dot". Physical Review Letters 88 (11): 117901. doi:10.1103/PhysRevLett.88.117901. ISSN 0031-9007. PMID 11909428. Bibcode: 2002PhRvL..88k7901C.
- ↑ Li, X. (2003). "An All-Optical Quantum Gate in a Semiconductor Quantum Dot". Science 301 (5634): 809–811. doi:10.1126/science.1083800. ISSN 0036-8075. PMID 12907794. Bibcode: 2003Sci...301..809L.
- ↑ Vektaris, G. (1994). "A new approach to the molecular biexciton theory". The Journal of Chemical Physics 101 (4): 3031–3040. doi:10.1063/1.467616. ISSN 0021-9606. Bibcode: 1994JChPh.101.3031V.
- ↑ "Fabrication of CuCl Quantum Dots and the Size Dependence of the Biexciton Binding Energy". Journal of the Korean Physical Society 37 (3): 309–312. 2000. http://www.jkps.or.kr/journal/view.html?uid=4106&vmd=Full.
- ↑ Liu, Jian-jun; Kong, Xiao-jun; Wei, Cheng-wen; Li, Shu-shen (1998). "Binding Energy of Biexcitons in Two-Dimensional Semiconductors". Chinese Physics Letters 15 (8): 588–590. doi:10.1088/0256-307X/15/8/016. ISSN 0256-307X. Bibcode: 1998ChPhL..15..588L.
- ↑ D. Bressanini; M. Mella; G. Morosi (1998). "Stability of four-body systems in three and two dimensions: A theoretical and quantum Monte Carlo study of biexciton molecules". Physical Review A 57 (6): 4956–4959. doi:10.1103/PhysRevA.57.4956. Bibcode: 1998PhRvA..57.4956B.
- ↑ M.Y.J. Tan; N.D. Drummond; R.J. Needs (2005). "Exciton and biexciton energies in bilayer systems". Physical Review B 71 (3): 033303. doi:10.1103/PhysRevB.71.033303. Bibcode: 2005PhRvB..71c3303T.
- ↑ R.M. Lee; N.D. Drummond; R.J. Needs (2009). "Exciton-exciton interaction and biexciton formation in bilayer systems". Physical Review B 79 (12): 125308. doi:10.1103/PhysRevB.79.125308. Bibcode: 2009PhRvB..79l5308L.
- ↑ M.Z. Mayers; T.C. Berkelbach; M.S. Hybertson; D.R. Reichman (2015). "Binding energies and spatial structures of small carrier complexes in monolayer transition-metal dichalcogenides via diffusion Monte Carlo". Physical Review B 92 (16): 161404. doi:10.1103/PhysRevB.92.161404. Bibcode: 2015PhRvB..92p1404M.
- ↑ Szyniszewski, M. (2017). "Binding energies of trions and biexcitons in two-dimensional semiconductors from diffusion quantum Monte Carlo calculations". Physical Review B 95 (8): 081301(R). doi:10.1103/PhysRevB.95.081301. Bibcode: 2017PhRvB..95h1301S.
- ↑ Mostaani, E. (2017). "Diffusion quantum Monte Carlo study of excitonic complexes in two-dimensional transition-metal dichalcogenides". Physical Review B 96 (7): 075431. doi:10.1103/PhysRevB.96.075431. Bibcode: 2017PhRvB..96g5431M.
- ↑ Pedersen, Thomas G.; Pedersen, Kjeld; Cornean, Horia D.; Duclos, Pierre (2005). "Stability and Signatures of Biexcitons in Carbon Nanotubes". Nano Letters 5 (2): 291–294. doi:10.1021/nl048108q. ISSN 1530-6984. PMID 15794613. Bibcode: 2005NanoL...5..291P.
- ↑ Colombier, L.; Selles, J.; Rousseau, E.; Lauret, J. S.; Vialla, F.; Voisin, C.; Cassabois, G. (2012). "Detection of a Biexciton in Semiconducting Carbon Nanotubes Using Nonlinear Optical Spectroscopy". Physical Review Letters 109 (19): 197402. doi:10.1103/PhysRevLett.109.197402. ISSN 0031-9007. PMID 23215424. Bibcode: 2012PhRvL.109s7402C. https://hal.archives-ouvertes.fr/hal-00750969/document.
- ↑ Masumoto, Yasuaki; Okamoto, Shinji; Katayanagi, Satoshi (1994). "Biexciton binding energy in CuCl quantum dots". Physical Review B 50 (24): 18658–18661. doi:10.1103/PhysRevB.50.18658. ISSN 0163-1829. PMID 9976308. Bibcode: 1994PhRvB..5018658M. https://tsukuba.repo.nii.ac.jp/?action=repository_action_common_download&item_id=15341&item_no=1&attribute_id=17&file_no=1.
 |