Physics:Exciton
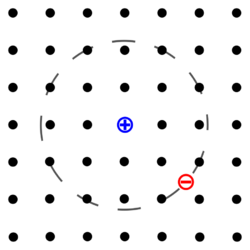
An electron and an electron hole that are attracted to each other by the Coulomb force can form a bound state called an exciton. It is an electrically neutral quasiparticle that exists mainly in condensed matter, including insulators, semiconductors, some metals, but also in certain atoms, molecules and liquids. The exciton is regarded as an elementary excitation that can transport energy without transporting net electric charge.[1][2][3][4]
An exciton can form when an electron from the valence band of a crystal is promoted in energy to the conduction band e.g., when a material absorbs a photon. Promoting the electron to the conduction band leaves a positively charged hole in the valence band. Here 'hole' represents the unoccupied quantum mechanical electron state with a positive charge, an analogue in crystal of a positron. Because of the attractive coulomb force between the electron and the hole, a bound state is formed, akin to that of the electron and proton in a hydrogen atom or the electron and positron in positronium. Excitons are composite bosons since they are formed from two fermions which are electron and hole.
The concept of excitons was first proposed by Yakov Frenkel in 1931,[5] when he described the excitation of an atomic lattice considering what is now called the tight-binding description of the band structure. In his model the electron and the hole bound by the coulomb interaction are located either on the same or on the nearest neighbouring sites of the lattice, but the exciton as a composite quasi-particle is able to travel through the lattice without any net transfer of charge, which lead to many propositions for optoelectronic devices.
Excitons are often treated in the two limiting cases:
(i) The small radius excitons, or Frenkel excitons, where the electron-hole relative distance is restricted to one or only a few nearest neighbour unit cells. Frenkel excitons typically occur in insulators and organic semiconductors with relatively narrow allowed energy bands and accordingly, rather heavy Effective mass.
(ii) the large radius excitons are called Wannier-Mott excitons, for which the relative motion of electron and hole in the crystal covers many unit cells. Wannier-Mott excitons are considered as hydrogen-like quasiparticles. The wavefunction of the bound state then is said to be hydrogenic, resulting in a series of energy states in analogy to a hydrogen atom. Compared to a hydrogen atom, the exciton binding energy in a crystal is much smaller and the exciton's size (radius) is much larger. This is mainly because of two effects: (a) Coulomb forces are screened in a crystal, which is expressed as a relative permittivity εr significantly larger than 1 and (b) the Effective mass of the electron and hole in a crystal are typically smaller compared to that of free electrons. Wannier-Mott excitons with binding energies ranging from a few to hundreds of meV, depending on the crystal, occur in many semiconductors including Cu2 O, GaAs, other III-V and II-VI semiconductors, transition metal dichalcogenides such as MoS2. Excitons give rise to spectrally narrow lines in optical absorption, reflection, transmission and luminescence spectra with the energies below the free-particle band gap of an insulator or a semiconductor. Exciton binding energy and radius can be extracted from optical absorption measurements in applied magnetic fields.[6]
The exciton as a quasiparticle is characterized by the momentum (or wavevectorK) describing free propagation of the electron-hole pair as a composite particle in the crystalline lattice in agreement with the Bloch theorem. The exciton energy depends on K and is typically parabolic for the wavevectors much smaller than the reciprocal lattice vector of the host lattice. The exciton energy also depends on the respective orientation of the electron and hole spins, whether they are parallel or anti-parallel. The spins are coupled by the exchange interaction, giving rise to exciton energy fine structure.
In metals and highly doped semiconductors a concept of the Gerald Mahan exciton is invoked where the hole in a valence band is correlated with the Fermi sea of conduction electrons. In that case no bound state in a strict sense is formed, but the Coulomb interaction leads to a significant enhancement of absorption in the vicinity of the fundamental absorption edge also known as the Mahan or Fermi-edge singularity.
Frenkel exciton
In materials with a relatively small dielectric constant, the Coulomb interaction between an electron and a hole may be strong and the excitons thus tend to be small, of the same order as the size of the unit cell. Molecular excitons may even be entirely located on the same molecule, as in fullerenes. This Frenkel exciton, named after Yakov Frenkel, has a typical binding energy on the order of 0.1 to 1 eV. Frenkel excitons are typically found in alkali halide crystals and in organic molecular crystals composed of aromatic molecules, such as anthracene and tetracene. Another example of Frenkel exciton includes on-site d-d excitations in transition metal compounds with partially filled d-shells. While d-d transitions are in principle forbidden by symmetry, they become weakly-allowed in a crystal when the symmetry is broken by structural relaxations or other effects. Absorption of a photon resonant with a d-d transition leads to the creation of an electron-hole pair on a single atomic site, which can be treated as a Frenkel exciton.
Wannier–Mott exciton
In semiconductors, the dielectric constant is generally large. Consequently, electric field screening tends to reduce the Coulomb interaction between electrons and holes. The result is a Wannier–Mott exciton,[7] which has a radius larger than the lattice spacing. Small effective mass of electrons that is typical of semiconductors also favors large exciton radii. As a result, the effect of the lattice potential can be incorporated into the effective masses of the electron and hole. Likewise, because of the lower masses and the screened Coulomb interaction, the binding energy is usually much less than that of a hydrogen atom, typically on the order of 0.01eV. This type of exciton was named for Gregory Wannier and Nevill Francis Mott. Wannier–Mott excitons are typically found in semiconductor crystals with small energy gaps and high dielectric constants, but have also been identified in liquids, such as liquid xenon. They are also known as large excitons.
In single-wall carbon nanotubes, excitons have both Wannier–Mott and Frenkel character. This is due to the nature of the Coulomb interaction between electrons and holes in one-dimension. The dielectric function of the nanotube itself is large enough to allow for the spatial extent of the wave function to extend over a few to several nanometers along the tube axis, while poor screening in the vacuum or dielectric environment outside of the nanotube allows for large (0.4 to 1.0eV) binding energies.
Often more than one band can be chosen as source for the electron and the hole, leading to different types of excitons in the same material. Even high-lying bands can be effective as femtosecond two-photon experiments have shown. At cryogenic temperatures, many higher excitonic levels can be observed approaching the edge of the band,[8] forming a series of spectral absorption lines that are in principle similar to hydrogen spectral series.
3D semiconductors
In a bulk semiconductor, a Wannier exciton has an energy and radius associated with it, called exciton Rydberg energy and exciton Bohr radius respectively.[9] For the energy, we have
- [math]\displaystyle{ E(n)=- \frac{ \left( \frac{\mu}{m_0 \varepsilon_r^2}\text{Ry} \right)}{n^2} \equiv -\frac{R_\text{X}}{n^2} }[/math]
where [math]\displaystyle{ \text{Ry} }[/math] is the Rydberg unit of energy (cf. Rydberg constant), [math]\displaystyle{ \varepsilon_r }[/math] is the (static) relative permittivity, [math]\displaystyle{ \mu= (m^*_e m^*_h)/(m^*_e+m^*_h) }[/math] is the reduced mass of the electron and hole, and [math]\displaystyle{ m_0 }[/math] is the electron mass. Concerning the radius, we have
- [math]\displaystyle{ r_n = \left(\frac{m_0 \varepsilon_r a_\text{H}}{\mu} \right)n^2 \equiv a_\text{X}n^2 }[/math]
where [math]\displaystyle{ a_\text{H} }[/math] is the Bohr radius.
For example, in GaAs, we have relative permittivity of 12.8 and effective electron and hole masses as 0.067m0 and 0.2m0 respectively; and that gives us [math]\displaystyle{ R_\text{X}=4.2 }[/math] meV and [math]\displaystyle{ a_\text{X}=13 }[/math] nm.
2D semiconductors
In two-dimensional (2D) materials, the system is quantum confined in the direction perpendicular to the plane of the material. The reduced dimensionality of the system has an effect on the binding energies and radii of Wannier excitons. In fact, excitonic effects are enhanced in such systems.[10]
For a simple screened Coulomb potential, the binding energies take the form of the 2D hydrogen atom[11]
- [math]\displaystyle{ E(n)= -\frac{R_\text{X}}{\left(n-\tfrac{1}{2}\right)^2} }[/math].
In most 2D semiconductors, the Rytova–Keldysh form is a more accurate approximation to the exciton interaction[12][13][14]
- [math]\displaystyle{ V(r)= -\frac{e^2}{8 \epsilon_0 r_0}\left[\text{H}_0\left(\frac{\kappa r}{r_0}\right)-Y_0\left(\frac{\kappa r}{r_0}\right)\right]. }[/math]
where [math]\displaystyle{ r_0 }[/math] is the so-called screening length, [math]\displaystyle{ \epsilon_0 }[/math] is the vacuum permittivity, [math]\displaystyle{ e }[/math] is the elementary charge, [math]\displaystyle{ \kappa }[/math] the average dielectric constant of the surrounding media, and [math]\displaystyle{ r }[/math] the exciton radius. For this potential, no general expression for the exciton energies may be found. One must instead turn to numerical procedures, and it is precisely this potential that gives rise to the nonhydrogenic Rydberg series of the energies in 2D semiconductors.[10]
Example: excitons in transition metal dichalcogenides (TMDs)
Monolayers of a transition metal dichalcogenide (TMD) are a good and cutting-edge example where excitons play a major role. In particular, in these systems, they exhibit a bounding energy of the order of 0.5 eV[2] with a Coulomb attraction between the hole and the electrons stronger than in other traditional quantum wells. As a result, optical excitonic peaks are present in these materials even at room temperatures.[2]
0D semiconductors
In nanoparticles which exhibit quantum confinement effects and hence behave as quantum dots (also called 0-dimensional semiconductors), excitonic radii are given by[15][16]
- [math]\displaystyle{ a_\text{X} = \frac{\varepsilon_r}{\mu/m_0}a_0 }[/math]
where [math]\displaystyle{ \varepsilon_r }[/math] is the relative permittivity, [math]\displaystyle{ \mu \equiv (m_e^*m_h^*)/(m_e^*+m_h^*) }[/math] is the reduced mass of the electron-hole system, [math]\displaystyle{ m_0 }[/math] is the electron mass, and [math]\displaystyle{ a_0 }[/math] is the Bohr radius.
Hubbard exciton
Hubbard excitons are linked to electrons not by a Coulomb's interaction, but by a magnetic force. Their name derives by the English physicist John Hubbard.
Hubbard excitons were observed for the first time in 2023 through the Terahertz time-domain spectroscopy. Those particles have been obtained by applying a light to a Mott antiferromagnetic insulator.[17]
Charge-transfer exciton
An intermediate case between Frenkel and Wannier excitons is the charge-transfer (CT) exciton. In molecular physics, CT excitons form when the electron and the hole occupy adjacent molecules.[18] They occur primarily in organic and molecular crystals;[19] in this case, unlike Frenkel and Wannier excitons, CT excitons display a static electric dipole moment. CT excitons can also occur in transition metal oxides, where they involve an electron in the transition metal 3d orbitals and a hole in the oxygen 2p orbitals. Notable examples include the lowest-energy excitons in correlated cuprates[20] or the two-dimensional exciton of TiO2.[21] Irrespective of the origin, the concept of CT exciton is always related to a transfer of charge from one atomic site to another, thus spreading the wave-function over a few lattice sites.
Surface exciton
At surfaces it is possible for so called image states to occur, where the hole is inside the solid and the electron is in the vacuum. These electron-hole pairs can only move along the surface.
Dark exciton
Dark excitons are those where the electrons have a different momentum from the holes to which they are bound that is they are in an optically forbidden transition which prevents them from photon absorption and therefore to reach their state they need phonon scattering. They can even outnumber normal bright excitons formed by absorption alone.[22][23][24]
Atomic and molecular excitons
Alternatively, an exciton may be described as an excited state of an atom, ion, or molecule, if the excitation is wandering from one cell of the lattice to another.
When a molecule absorbs a quantum of energy that corresponds to a transition from one molecular orbital to another molecular orbital, the resulting electronic excited state is also properly described as an exciton. An electron is said to be found in the lowest unoccupied orbital and an electron hole in the highest occupied molecular orbital, and since they are found within the same molecular orbital manifold, the electron-hole state is said to be bound. Molecular excitons typically have characteristic lifetimes on the order of nanoseconds, after which the ground electronic state is restored and the molecule undergoes photon or phonon emission. Molecular excitons have several interesting properties, one of which is energy transfer (see Förster resonance energy transfer) whereby if a molecular exciton has proper energetic matching to a second molecule's spectral absorbance, then an exciton may transfer (hop) from one molecule to another. The process is strongly dependent on intermolecular distance between the species in solution, and so the process has found application in sensing and molecular rulers.
The hallmark of molecular excitons in organic molecular crystals are doublets and/or triplets of exciton absorption bands strongly polarized along crystallographic axes. In these crystals an elementary cell includes several molecules sitting in symmetrically identical positions, which results in the level degeneracy that is lifted by intermolecular interaction. As a result, absorption bands are polarized along the symmetry axes of the crystal. Such multiplets were discovered by Antonina Prikhot'ko[25][26] and their genesis was proposed by Alexander Davydov. It is known as 'Davydov splitting'.[27][28]
Giant oscillator strength of bound excitons
Excitons are lowest excited states of the electronic subsystem of pure crystals. Impurities can bind excitons, and when the bound state is shallow, the oscillator strength for producing bound excitons is so high that impurity absorption can compete with intrinsic exciton absorption even at rather low impurity concentrations. This phenomenon is generic and applicable both to the large radius (Wannier–Mott) excitons and molecular (Frenkel) excitons. Hence, excitons bound to impurities and defects possess giant oscillator strength.[29]
Self-trapping of excitons
In crystals, excitons interact with phonons, the lattice vibrations. If this coupling is weak as in typical semiconductors such as GaAs or Si, excitons are scattered by phonons. However, when the coupling is strong, excitons can be self-trapped.[30][31] Self-trapping results in dressing excitons with a dense cloud of virtual phonons which strongly suppresses the ability of excitons to move across the crystal. In simpler terms, this means a local deformation of the crystal lattice around the exciton. Self-trapping can be achieved only if the energy of this deformation can compete with the width of the exciton band. Hence, it should be of atomic scale, of about an electron volt.
Self-trapping of excitons is similar to forming strong-coupling polarons but with three essential differences. First, self-trapped exciton states are always of a small radius, of the order of lattice constant, due to their electric neutrality. Second, there exists a self-trapping barrier separating free and self-trapped states, hence, free excitons are metastable. Third, this barrier enables coexistence of free and self-trapped states of excitons.[32][33][34] This means that spectral lines of free excitons and wide bands of self-trapped excitons can be seen simultaneously in absorption and luminescence spectra. While the self-trapped states are of lattice-spacing scale, the barrier has typically much larger scale. Indeed, its spatial scale is about [math]\displaystyle{ r_b\sim m\gamma^2/\omega^2 }[/math] where [math]\displaystyle{ m }[/math] is effective mass of the exciton, [math]\displaystyle{ \gamma }[/math] is the exciton-phonon coupling constant, and [math]\displaystyle{ \omega }[/math] is the characteristic frequency of optical phonons. Excitons are self-trapped when [math]\displaystyle{ m }[/math] and [math]\displaystyle{ \gamma }[/math] are large, and then the spatial size of the barrier is large compared with the lattice spacing. Transforming a free exciton state into a self-trapped one proceeds as a collective tunneling of coupled exciton-lattice system (an instanton). Because [math]\displaystyle{ r_b }[/math] is large, tunneling can be described by a continuum theory.[35] The height of the barrier [math]\displaystyle{ W\sim \omega^4/m^3\gamma^4 }[/math]. Because both [math]\displaystyle{ m }[/math] and [math]\displaystyle{ \gamma }[/math] appear in the denominator of [math]\displaystyle{ W }[/math], the barriers are basically low. Therefore, free excitons can be seen in crystals with strong exciton-phonon coupling only in pure samples and at low temperatures. Coexistence of free and self-trapped excitons was observed in rare-gas solids,[36][37] alkali-halides,[38] and in molecular crystal of pyrene.[39]
Interaction
Excitons are the main mechanism for light emission in semiconductors at low temperature (when the characteristic thermal energy kT is less than the exciton binding energy), replacing the free electron-hole recombination at higher temperatures.
The existence of exciton states may be inferred from the absorption of light associated with their excitation. Typically, excitons are observed just below the band gap.
When excitons interact with photons a so-called polariton (or more specifically exciton-polariton) is formed. These excitons are sometimes referred to as dressed excitons.
Provided the interaction is attractive, an exciton can bind with other excitons to form a biexciton, analogous to a dihydrogen molecule. If a large density of excitons is created in a material, they can interact with one another to form an electron-hole liquid, a state observed in k-space indirect semiconductors.
Additionally, excitons are integer-spin particles obeying Bose statistics in the low-density limit. In some systems, where the interactions are repulsive, a Bose–Einstein condensed state, called excitonium, is predicted to be the ground state. Some evidence of excitonium has existed since the 1970s but has often been difficult to discern from a Peierls phase.[40] Exciton condensates have allegedly been seen in a double quantum well systems.[41] In 2017 Kogar et al. found "compelling evidence" for observed excitons condensing in the three-dimensional semimetal 1T-TiSe2.[42]
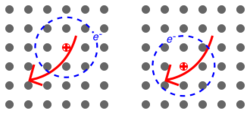
Spatially direct and indirect excitons
Normally, excitons in a semiconductor have a very short lifetime due to the close proximity of the electron and hole. However, by placing the electron and hole in spatially separated quantum wells with an insulating barrier layer in between so called 'spatially indirect' excitons can be created. In contrast to ordinary (spatially direct), these spatially indirect excitons can have large spatial separation between the electron and hole, and thus possess a much longer lifetime.[43] This is often used to cool excitons to very low temperatures in order to study Bose–Einstein condensation (or rather its two-dimensional analog).[44]
See also
References
- ↑ R. S. Knox, Theory of excitons, Solid state physics (Ed. by Seitz and Turnbul), New York, New York: Academic, v. 5, 1963.
- ↑ Jump up to: 2.0 2.1 2.2 Mueller, Thomas; Malic, Ermin (2018-09-10). "Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors" (in en). npj 2D Materials and Applications 2 (1): 1–12. doi:10.1038/s41699-018-0074-2. ISSN 2397-7132.
- ↑ Monique Combescot and Shiue-Yuan Shiau, "Excitons and Cooper Pairs: Two Composite Bosons in Many-Body Physics", Oxford University Press. ISBN:9780198753735.
- ↑ Fox, Mark (2010-03-25) (in en-uk). Optical Properties of Solids (2nd ed.). Oxford Master Series in Physics.
- ↑ Frenkel, J. (1931). "On the Transformation of light into Heat in Solids. I". Physical Review 37 (1): 17. doi:10.1103/PhysRev.37.17. Bibcode: 1931PhRv...37...17F.
- ↑ Arora, Ashish (30 March 2021). "Magneto-optics of layered two-dimensional semiconductors and heterostructures: Progress and prospects". Journal of Applied Physics 129 (12). doi:10.1063/5.0042683. https://doi.org/10.1063/5.0042683.
- ↑ Wannier, Gregory (1937). "The Structure of Electronic Excitation Levels in Insulating Crystals". Physical Review 52 (3): 191. doi:10.1103/PhysRev.52.191. Bibcode: 1937PhRv...52..191W.
- ↑ Kazimierczuk, T.; Fröhlich, D.; Scheel, S.; Stolz, H.; Bayer, M. (2014). "Giant Rydberg excitons in the copper oxide Cu2O". Nature 514 (7522): 343–347. doi:10.1038/nature13832. PMID 25318523. Bibcode: 2014Natur.514..343K.
- ↑ Fox, Mark (2010-03-25). Optical Properties of Solids. Oxford Master Series in Physics (2 ed.). Oxford University Press. p. 97. ISBN 978-0199573363. https://global.oup.com/academic/product/optical-properties-of-solids-9780199573370?q=max%20fox%20optical%20properties%20of%20solids&lang=en&cc=no.
- ↑ Jump up to: 10.0 10.1 Chernikov, Alexey; Berkelbach, Timothy C.; Hill, Heather M.; Rigosi, Albert; Li, Yilei; Aslan, Ozgur Burak; Reichman, David R.; Hybertsen, Mark S. et al. (2014). "Exciton Binding Energy and Nonhydrogenic Rydberg Series in MonolayerWS2". Physical Review Letters 113 (7): 076802. doi:10.1103/PhysRevLett.113.076802. ISSN 0031-9007. PMID 25170725. Bibcode: 2014PhRvL.113g6802C.
- ↑ Yang, X. L. (1 February 1991). "Analytic solution of a two-dimensional hydrogen atom. I. Nonrelativistic theory". Physical Review A 43 (3): 1186–1196. doi:10.1103/PhysRevA.43.1186. PMID 9905143. Bibcode: 1991PhRvA..43.1186Y. https://link.aps.org/doi/10.1103/PhysRevA.43.1186.
- ↑ Rytova, N S. (1967). "The screened potential of a point charge in a thin film". Proc. MSU Phys. Astron. 3: 30.
- ↑ Keldysh, LV (1979). "Coulomb interaction in thin semiconductor and semimetal films". JETP Lett. 29: 658.
- ↑ Trolle, Mads L.; Pedersen, Thomas G.; Véniard, Valerie (2017). "Model dielectric function for 2D semiconductors including substrate screening". Sci. Rep. 7: 39844. doi:10.1038/srep39844. PMID 28117326. Bibcode: 2017NatSR...739844T.
- ↑ Brus, Louis (1986). "Electronic wave functions in semiconductor clusters: experiment and theory". The Journal of Physical Chemistry (ACS Publications) 90 (12): 2555–2560. doi:10.1021/j100403a003.
- ↑ Edvinsson, T. (2018). "Optical quantum confinement and photocatalytic properties in two-, one- and zero-dimensional nanostructures". Royal Society Open Science 5 (9): 180387. doi:10.1098/rsos.180387. ISSN 2054-5703. PMID 30839677. Bibcode: 2018RSOS....580387E.
- ↑ "Scientists observe Hubbard exciton in strongly correlated insulators". Phys.org. September 25, 2023. doi:10.1038/s41567-023-02204-2. https://archive.today/20231011073541/https://phys.org/news/2023-09-scientists-hubbard-exciton-strongly-insulators.html.
- ↑ Wright, J. D. (1995) (in en-uk). Molecular Crystals (2nd ed.). Cambridge University Press. p. 108. ISBN 978-0-521-47730-7. https://books.google.com/books?id=7sroAgMASIEC&pg=PA108.
- ↑ Lanzani, Guglielmo (2012) (in en). The Photophysics Behind Photovoltaics and Photonics. Wiley-VCH Verlag. p. 82. https://books.google.com/books?id=RVyvgKo0lGQC&pg=PA82.
- ↑ Ellis, D. S.; Hill, J. P.; Wakimoto, S.; Birgeneau, R. J.; Casa, D.; Gog, T.; Kim, Young-June (2008). "Charge-transfer exciton in La2CuO4 probed with resonant inelastic x-ray scattering". Physical Review B 77 (6): 060501(R). doi:10.1103/PhysRevB.77.060501. Bibcode: 2008PhRvB..77f0501E.
- ↑ Baldini, Edoardo; Chiodo, Letizia; Dominguez, Adriel; Palummo, Maurizia; Moser, Simon; Yazdi-Rizi, Meghdad; Aubock, Gerald; Mallett, Benjamin P P et al. (2017). "Strongly bound excitons in anatase TiO2 single crystals and nanoparticles". Nature Communications 8 (13): 13. doi:10.1038/s41467-017-00016-6. PMID 28408739. Bibcode: 2017NatCo...8...13B.
- ↑ Madéo, Julien; Man, Michael K. L.; Sahoo, Chakradhar; Campbell, Marshall; Pareek, Vivek; Wong, E. Laine; Al-Mahboob, Abdullah; Chan, Nicholas S. et al. (2020-12-04). "Directly visualizing the momentum-forbidden dark excitons and their dynamics in atomically thin semiconductors" (in en). Science 370 (6521): 1199–1204. doi:10.1126/science.aba1029. ISSN 0036-8075. https://www.science.org/doi/10.1126/science.aba1029.
- ↑ "Dark excitons hit the spotlight" (in en). 2020-12-04. https://www.oist.jp/news-center/news/2020/12/4/dark-excitons-hit-spotlight.
- ↑ "Dark excitons outnumber bright ones" (in en). Physics Today 2021 (1): 0107a. 2021-01-07. doi:10.1063/PT.6.1.20210107a. https://pubs.aip.org/physicstoday/online/30231.
- ↑ A. Prikhotjko, Absorption Spectra of Crystals at Low Temperatures, J. Physics USSR 8, p. 257 (1944).
- ↑ A. F. Prikhot'ko, Izv, AN SSSR Ser. Fiz. 7, p. 499 (1948) http://ujp.bitp.kiev.ua/files/journals/53/si/53SI18p.pdf .
- ↑ A. S. Davydov, Theory of Molecular Excitons (Plenum, New York, New York) 1971.
- ↑ V. L. Broude, E. I. Rashba, and E. F. Sheka, Spectroscopy of molecular excitons (Springer, New York, New York) 1985.
- ↑ E. I. Rashba, Giant Oscillator Strengths Associated with Exciton Complexes, Soviet Physics Semiconductors 8, 807–816 (1975).
- ↑ N. Schwentner, E.-E. Koch, and J. Jortner, Electronic excitations in condensed rare gases, Springer tracts in modern physics, 107, p. 1 (1985).
- ↑ M. Ueta, H. Kanzaki, K. Kobayashi, Y. Toyozawa, and E. Hanamura. Excitonic Processes in Solids, Springer Series in Solid State Sciences, Vol. 60 (1986).
- ↑ E. I. Rashba, "Theory of Strong Interaction of Electron Excitations with Lattice Vibrations in Molecular Crystals", Optika i Spektroskopiya 2, pp. 75, 88 (1957).
- ↑ E. I. Rashba, Self-trapping of excitons, in: Excitons (North-Holland, Amsterdam, 1982), p. 547.
- ↑ S. I. Pekar, E. I. Rashba, V. I. Sheka, Soviet Physics JETP 49, p. 251 (1979), http://www.jetp.ac.ru/cgi-bin/dn/e_049_01_0129.pdf .
- ↑ Kagan, Yu; Leggett, A. J. (2012-12-02) (in en). Quantum Tunnelling in Condensed Media. Elsevier. ISBN 978-0-444-60047-9. https://books.google.com/books?id=ElDtL9qZuHUC&dq=%22E+I+Rashba%22&pg=PA347.
- ↑ Grassano, U. M., ed (1987) (in en). Excited-state spectroscopy in solids: Varenna on Lake Como, Villa Monastero, 9–19 July 1985. Proceedings of the International School of Physics "Enrico Fermi". Amsterdam ; New York: North-Holland. Course 96. ISBN 978-0-444-87070-4. https://searchworks.stanford.edu/view/1269574.
- ↑ I. Ya. Fugol', "Free and self-trapped excitons in cryocrystals: kinetics and relaxation processes." Advances in Physics 37, pp. 1–35 (1988).
- ↑ Ch. B. Lushchik, in "Excitons," edited by E. I. Rashba, and M. D. Sturge, (North Holland, Amsterdam, 1982), p. 505.
- ↑ M. Furukawa, Ken-ichi Mizuno, A. Matsui, N. Tamai and I. Yamazaiu, Branching of Exciton Relaxation to the Free and Self-Trapped Exciton States, Chemical Physics 138, p. 423 (1989).
- ↑ "New form of matter 'excitonium' discovered". The Times of India. https://timesofindia.indiatimes.com/home/science/new-form-of-matter-excitonium-discovered/articleshow/61994947.cms.
- ↑ Eisenstein, J. P. (January 10, 2014). "Exciton Condensation in Bilayer Quantum Hall Systems". Annual Review of Condensed Matter Physics 5: 159–181. doi:10.1146/annurev-conmatphys-031113-133832. Bibcode: 2014ARCMP...5..159E.
- ↑ .Kogar, Anshul; Rak, Melinda S; Vig, Sean; Husain, Ali A; Flicker, Felix; Joe, Young Il; Venema, Luc; MacDougall, Greg J. et al. (2017). "Signatures of exciton condensation in a transition metal dichalcogenide". Science 358 (6368): 1314–1317. doi:10.1126/science.aam6432. PMID 29217574. Bibcode: 2017Sci...358.1314K.
- ↑ Merkl, P.; Mooshammer, F.; Steinleitner, P.; Girnghuber, A.; Lin, K.-Q.; Nagler, P.; Holler, J.; Schüller, C. et al. (2019). "Ultrafast transition between exciton phases in van der Waals heterostructures". Nature Materials 18 (7): 691–696. doi:10.1038/s41563-019-0337-0. PMID 30962556. Bibcode: 2019NatMa..18..691M.
- ↑ High, A. A.; Leonard, J. R.; Hammack, A. T.; Fogler, M. M.; Butov, L. V.; Kavokin, A. V.; Campman, K. L.; Gossard, A. C. (2012). "Spontaneous coherence in a cold exciton gas". Nature 483 (7391): 584–588. doi:10.1038/nature10903. PMID 22437498. Bibcode: 2012Natur.483..584H.
 |