Physics:Permeation

Short description: Penetration of a liquid, gas, or vapor through a solid

In physics and engineering, permeation (also called imbuing) is the penetration of a permeate (a fluid such as a liquid, gas, or vapor) through a solid. It is directly related to the concentration gradient of the permeate, a material's intrinsic permeability, and the materials' mass diffusivity. Permeation is modeled by equations such as Fick's laws of diffusion, and can be measured using tools such as a minipermeameter.

Description

The process of permeation involves the diffusion of molecules, called the permeant, through a membrane or interface. Permeation works through diffusion; the permeant will move from high concentration to low concentration across the interface. A material can be semipermeable, with the presence of a semipermeable membrane. Only molecules or ions with certain properties will be able to diffuse across such a membrane. This is a very important mechanism in biology where fluids inside a blood vessel need to be regulated and controlled. Permeation can occur through most materials including metals, ceramics and polymers. However, the permeability of metals is much lower than that of ceramics and polymers due to their crystal structure and porosity.

Permeation is something that must be considered carefully in many polymer applications, due to their high permeability. Permeability depends on the temperature of the interaction as well as the characteristics of both the polymer and the permeant component. Through the process of sorption, molecules of the permeant can be either absorbed or desorbed at the interface. The permeation of a material can be measured through numerous methods that quantify the permeability of a substance through a specific material.

Permeability due to diffusion is measured in SI units of mol/(m･s･Pa) although Barrers are also commonly used. Permeability due to diffusion is not to be confused with Permeability (earth sciences) due to fluid flow in porous solids measured in Darcy.

Related terms

• Permeant: The substance or species, ion, molecules permeating through the solid.
• Semipermeability: Property of a material to be permeable only for some substances and not for others.
• Permeation measurement: Method for the quantification of the permeability of a material for a specific substance.

History

Abbé Jean-Antoine Nollet (physicist, 1700–1770)

Nollet tried to seal wine containers with a pig's bladder and stored them under water. After a while the bladder bulged outwards. He noticed the high pressure that discharged after he pierced the bladder. Curious, he did the experiment the other way round: he filled the container with water and stored it in wine. The result was a bulging inwards of the bladder. His notes about this experiment are the first scientific mention of permeation (later it would be called semipermeability).

Thomas Graham (chemist, 1805–1869)

Graham experimentally proved the dependency of gas diffusion on molecular weight, which is now known as Graham's law.

Richard Barrer (1910–1996)

Barrer developed the modern Barrer measurement technique, and first used scientific methods for measuring permeation rates.

Applications

• Packaging: The permeability of the package (materials, seals, closures, etc.) needs to be matched with the sensitivity of the package contents and the specified shelf life. Some packages must have nearly hermetic seals while others can (and sometimes must) be selectively permeable. Knowledge about the exact permeation rates is therefore essential.

Fuel Cell Configuration

• Tires: Air pressure in tires should decrease as slowly as possible. A good tire is one that allows the least amount of gas to escape. Permeation will occur over time with the tires, so it is best to know the permeability of the material that will make up the tire with the desired gas to make the most efficient tires.
• Insulating material: Water vapour permeation of insulating material is important as well as for submarine cables to protect the conductor from corrosion.
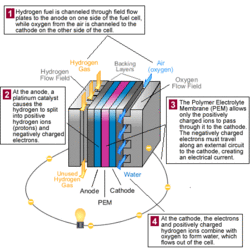
• Fuel cells: Automobiles are equipped with Polymer Electrolyte Membrane (PEM) fuel cells to convert hydrogen fuel and oxygen found in the atmosphere to produce electricity. However, these cells only produce around 1.16 volts of electricity. In order to power a vehicle, multiple cells are arranged into a stack. A stack's power output depends on both the number and the size of the individual fuel cells.
• Thermoplastic and Thermosetting Piping: Pipes intended to transport water under high pressure can be considered as failed when there is a detectable permeation of water through the pipe wall to the outer surface of the pipe.
• Medical Uses: Permeation can also be seen in the medical field in drug delivery. Drug patches made up of polymer material contain a chemical reservoir that is loaded beyond its solubility, and then transferred to the body through contact. In order for the chemical to release itself into the body, it must permeate and diffuse through the polymer membrane, according to the concentration gradient. Due to the over solubility of the reservoir, transport of the drug follows the burst and lag mechanism. There is a high transfer rate of the drug when the patch makes contact with the skin, but as time increases a concentration gradient is established, meaning delivery of the drug settles to a constant rate. This is crucial in drug delivery and is used in cases such as the Ocusert System. But also the opposite case can be found in the medical field. As ampoules may contain highly sensitive pharmaceuticals for injection it is crucial that the used material prevents any kinds of substances to enter the pharmaceutical product or evaporate from it. For this, ampoules are often made from glass and less frequently from synthetic materials.
• Technical uses: At the production of Halogen Lamps, halogen gases have to be encapsulated very closely. Aluminosilicate glass can be the perfect barrier for the gas encapsulation. Hereby, the transition to the electrode is critical. But due to matching thermal expansions of the glass body and the metal, the transition is working.

Permeation measurement

thumb|Permeation measurement with sweep gas

The permeation of films and membranes can be measured with any gas or liquid. One method uses a central module which is separated by the test film: the testing gas is fed on the one side of the cell and the permeated gas is carried to the detector by a sweep gas. The diagram on the right shows a testing cell for films, normally made from metals like stainless steel. The photo shows a testing cell for pipes made from glass, similar to a Liebig condenser. The testing medium (liquid or gas) is situated in the inner white pipe and the permeate is collected in the space between the pipe and the glass wall. It is transported by a sweep gas (connected to the upper and lower joint) to an analysing device.

Permeation can also be measured through intermittent contact. This method involves taking a sample of the test chemical and placing it on the surface of the material whose permeability is being observed while adding or removing specific amounts of the test chemical. After a known amount of time, the material is analyzed to find the concentration of the test chemical present throughout its structure. Along with the amount of time the chemical was on the material and the analysis of the test material, one can determine the cumulative permeation of the test chemical.

The following table gives examples of the calculated permeability coefficient of certain gases through a silicone membrane.

Gas Name	Chemical Formula	Silicone Permeability Coefficient (Barrer)*
Oxygen	O2	600
Hydrogen	H2	650
Carbon Dioxide	CO2	3250
Methanol	CH3OH	13900
Water	H2O	36000

*1 Barrer = 10⁻¹⁰ cm³ (STP) · cm /cm² · s · cm-Hg

Unless otherwise noted, permeabilities are measured and reported at 25 °C (RTP) and not (STP) From W. L. Robb. Thin Silicone Membranes – Their Permeation Properties and Some Applications. Annals of the New York Academy of Sciences, vol. 146, (January 1968) issue 1 Materials in, pp. 119–137

Approximation using Fick's First law

The flux or flow of mass of the permeate through the solid can be modeled by Fick's first law.

[math]\displaystyle{ \bigg. J = - D \frac{\partial \phi}{\partial x} \bigg. }[/math]

This equation can be modified to a very simple formula that can be used in basic problems to approximate permeation through a membrane.

[math]\displaystyle{ \bigg. J = - D \frac{(C_2 - C_1)}{\delta} \bigg. }[/math]

where

• [math]\displaystyle{ J }[/math] is the "diffusion flux"
• [math]\displaystyle{ \, D }[/math] is the diffusion coefficient or mass diffusivity
• [math]\displaystyle{ C }[/math] is the concentration of the permeate
• [math]\displaystyle{ \, \delta }[/math] is the thickness of the membrane

We can introduce [math]\displaystyle{ S }[/math] into this equation, which represents the sorption equilibrium parameter, which is the constant of proportionality between pressure ([math]\displaystyle{ p }[/math]) and [math]\displaystyle{ C }[/math]. This relationship can be represented as [math]\displaystyle{ C=Sp }[/math].

[math]\displaystyle{ \bigg. J = - D \frac{S(p_2 - p_1)}{\delta} \bigg. }[/math]

The diffusion coefficient can be combined with the sorption equilibrium parameter to get the final form of the equation, where [math]\displaystyle{ P }[/math] is the permeability of the membrane. The relationship being [math]\displaystyle{ P = SD }[/math]

[math]\displaystyle{ \bigg. J = -\frac{P(p_2 - p_1)}{\delta} \bigg. }[/math]

Solubility of a gas in a metal

In practical applications when looking at gases permeating metals, there is a way to relate gas pressure to concentration. Many gases exist as diatomic molecules when in the gaseous phase, but when permeating metals they exist in their singular ionic form. Sieverts' law states that the solubility of a gas, in the form of a diatomic molecule, in metal is proportional to the square root of the partial pressure of the gas.

The flux can be approximated in this case by the equation

[math]\displaystyle{ \bigg. J = - D \frac{(S_1 - S_2)}{\delta} \bigg. }[/math]

We can introduce [math]\displaystyle{ K }[/math] into this equation, which represents the reaction equilibrium constant. From the relationship [math]\displaystyle{ S = {K \sqrt{p_N}} }[/math].

[math]\displaystyle{ \bigg. J = - D \frac{K(\sqrt{p_1} - \sqrt{p_2})}{\delta} \bigg. }[/math]

The diffusion coefficient can be combined with the reaction equilibrium constant to get the final form of the equation, where [math]\displaystyle{ P }[/math] is the permeability of the membrane. The relationship being [math]\displaystyle{ P = KD }[/math]

[math]\displaystyle{ \bigg. J = - \frac{P(\sqrt{p_1} - \sqrt{p_2})}{\delta} \bigg. }[/math]

See also

• Engineering:Moisture vapor transmission rate – Measure of the passage of water vapor through a substance
• Oxygen transmission rate
• Earth:Permeability (earth sciences)

Further reading

• Yam, K. L., Encyclopedia of Packaging Technology, John Wiley & Sons, 2009, ISBN:978-0-470-08704-6
• Massey, L K, Permeability Properties of Plastics and Elastomers, 2003, Andrew Publishing, ISBN:978-1-884207-97-6
• ASTM F1249 Standard Test Method for Water Vapor Transmission Rate Through Plastic Film and Sheeting Using a Modulated Infrared Sensor
• ASTM E398 Standard Test Method for Water Vapor Transmission Rate of Sheet Materials Using Dynamic Relative Humidity Measurement
• ASTM F2298 Standard Test Methods for Water Vapor Diffusion Resistance and Air Flow Resistance of Clothing Materials Using the Dynamic Moisture Permeation Cell
• F2622 Standard Test Method for Oxygen Gas Transmission Rate Through Plastic Film and Sheeting Using Various Sensors
• G1383: Standard Test Method for Permeation of Liquids and Gases through Protective Clothing Materials under Conditions of Intermittent Contact.
• "Thin silicone membranes – Their permeation properties and some applications", Annals of the New York Academy of Sciences, vol. 146, issue 1 Materials in, pp. 119–137 W. L. Robb
• Pharmaceutical Systems for Drug Delivery, David Jones; Chien YW. 2nd ed. New York: Marcel Dekker, Inc; 1993. Novel drug delivery systems.
• O.V. Malykh, A.Yu. Golub, V.V. Teplyakov, "Polymeric membrane materials: New aspects of empirical approaches to prediction of gas permeability parameters in relation to permanent gases, linear lower hydrocarbons and some toxic gases", Advances in Colloid and Interface Science, Volume 165, Issues 1–2, 11 May 2011, Pages 89–99 doi:10.1016/j.cis.2010.10.004.
• Prediction of Mass Permeation in Polymers (and their Composites) based on Free Volume Theory and Sanchez-Lacombe Equation of State, CheFEM software.