Physics:Emden–Chandrasekhar equation

Numerical solution of Emden–Chandrasekhar equation

In astrophysics, the Emden–Chandrasekhar equation is a dimensionless form of the Poisson equation for the density distribution of a spherically symmetric isothermal gas sphere subjected to its own gravitational force, named after Robert Emden and Subrahmanyan Chandrasekhar. The equation was first introduced by Robert Emden in 1907. The equation reads

[math]\displaystyle{ \frac{1}{\xi^2} \frac{d}{d\xi}\left(\xi^2 \frac{d\psi}{d\xi}\right)= e^{-\psi} }[/math]

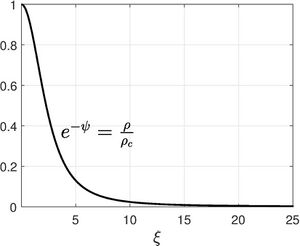
where [math]\displaystyle{ \xi }[/math] is the dimensionless radius and [math]\displaystyle{ \psi }[/math] is the related to the density of the gas sphere as [math]\displaystyle{ \rho=\rho_c e^{-\psi} }[/math], where [math]\displaystyle{ \rho_c }[/math] is the density of the gas at the centre. The equation has no known explicit solution. If a polytropic fluid is used instead of an isothermal fluid, one obtains the Lane–Emden equation. The isothermal assumption is usually modeled to describe the core of a star. The equation is solved with the initial conditions,

[math]\displaystyle{ \psi =0, \quad \frac{d\psi}{d\xi} =0 \quad \text{at} \quad \xi=0. }[/math]

The equation appears in other branches of physics as well, for example the same equation appears in the Frank-Kamenetskii explosion theory for a spherical vessel. The relativistic version of this spherically symmetric isothermal model was studied by Subrahmanyan Chandrasekhar in 1972.

Derivation

For an isothermal gaseous star, the pressure [math]\displaystyle{ p }[/math] is due to the kinetic pressure and radiation pressure

[math]\displaystyle{ p = \rho\frac{k_B}{W H} T + \frac{4\sigma}{3c} T^4 }[/math]

whe

• [math]\displaystyle{ \rho }[/math] is the density
• [math]\displaystyle{ k_B }[/math] is the Boltzmann constant
• [math]\displaystyle{ W }[/math] is the mean molecular weight
• [math]\displaystyle{ H }[/math] is the mass of the proton
• [math]\displaystyle{ T }[/math] is the temperature of the star
• [math]\displaystyle{ \sigma }[/math] is the Stefan–Boltzmann constant
• [math]\displaystyle{ c }[/math] is the speed of light

The equation for equilibrium of the star requires a balance between the pressure force and gravitational force

[math]\displaystyle{ \frac{1}{r^2} \frac{d}{dr} \left(\frac{r^2}{\rho}\frac{dp}{dr}\right)= - 4\pi G \rho }[/math]

where [math]\displaystyle{ r }[/math] is the radius measured from the center and [math]\displaystyle{ G }[/math] is the gravitational constant. The equation is re-written as

[math]\displaystyle{ \frac{k_B T}{WH}\frac{1}{r^2} \frac{d}{dr} \left(r^2\frac{d \ln \rho}{dr} \right) = - 4\pi G \rho }[/math]

Actual solution and asymptotic solution

Introducing the transformation

[math]\displaystyle{ \psi = \ln \frac{\rho_c}{\rho}, \quad \xi = r \left(\frac{4\pi G \rho_c W H}{k_B T}\right)^{1/2} }[/math]

where [math]\displaystyle{ \rho_c }[/math] is the central density of the star, leads to

[math]\displaystyle{ \frac{1}{\xi^2} \frac{d}{d\xi}\left(\xi^2 \frac{d\psi}{d\xi}\right)= e^{-\psi} }[/math]

The boundary conditions are

[math]\displaystyle{ \psi =0, \quad \frac{d\psi}{d\xi} =0 \quad \text{at} \quad \xi=0 }[/math]

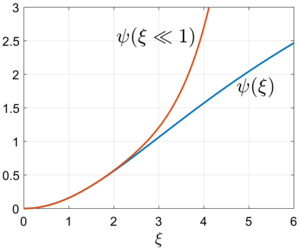
For [math]\displaystyle{ \xi\ll 1 }[/math], the solution goes like

[math]\displaystyle{ \psi = \frac{\xi^2}{6} - \frac{\xi^4}{120} + \frac{\xi^6}{1890} + \cdots }[/math]

Limitations of the model

Assuming isothermal sphere has some disadvantages. Though the density obtained as solution of this isothermal gas sphere decreases from the centre, it decreases too slowly to give a well-defined surface and finite mass for the sphere. It can be shown that, as [math]\displaystyle{ \xi \gg 1 }[/math],

[math]\displaystyle{ \frac{\rho}{\rho_c}=e^{-\psi}=\frac{2}{\xi^2} \left[1+\frac{A}{\xi^{1/2}} \cos\left(\frac{\sqrt 7}{2}\ln \xi + \delta\right) + O(\xi^{-1})\right] }[/math]

where [math]\displaystyle{ A }[/math] and [math]\displaystyle{ \delta }[/math] are constants which will be obtained with numerical solution. This behavior of density gives rise to increase in mass with increase in radius. Thus, the model is usually valid to describe the core of the star, where the temperature is approximately constant.

Singular solution

Introducing the transformation [math]\displaystyle{ x=1/\xi }[/math] transforms the equation to

[math]\displaystyle{ x^4 \frac{d^2\psi}{dx^2} = e^{-\psi} }[/math]

The equation has a singular solution given by

[math]\displaystyle{ e^{-\psi_s} = 2x^2, \quad \text{or} \quad -\psi_s = 2 \ln x+ \ln 2 }[/math]

Therefore, a new variable can be introduced as [math]\displaystyle{ -\psi = 2 \ln x + z }[/math], where the equation for [math]\displaystyle{ z }[/math] can be derived,

[math]\displaystyle{ \frac{d^2z}{dt^2}-\frac{dz}{dt}+ e^z -2 =0, \quad \text{where} \quad t=\ln x }[/math]

This equation can be reduced to first order by introducing

[math]\displaystyle{ y=\frac{dz}{dt} = \xi \frac{d\psi}{d\xi} - 2 }[/math]

then we have

[math]\displaystyle{ y\frac{dy}{dz} - y + e^z- 2 = 0 }[/math]

Reduction

There is another reduction due to Edward Arthur Milne. Let us define

[math]\displaystyle{ u = \frac{\xi e^{-\psi}}{d\psi/d\xi}, \quad v = \xi \frac{d\psi}{d\xi} }[/math]

then

[math]\displaystyle{ \frac{u}{v}\frac{dv}{du} = -\frac{u-1}{u+v-3} }[/math]

Properties

• If [math]\displaystyle{ \psi(\xi) }[/math] is a solution to Emden–Chandrasekhar equation, then [math]\displaystyle{ \psi(A\xi)-2\ln A }[/math] is also a solution of the equation, where [math]\displaystyle{ A }[/math] is an arbitrary constant.
• The solutions of the Emden–Chandrasekhar equation which are finite at the origin have necessarily [math]\displaystyle{ d\psi/d\xi=0 }[/math] at [math]\displaystyle{ \xi=0 }[/math]

See also

• Lane–Emden equation
• Frank-Kamenetskii theory
• Chandrasekhar's white dwarf equation