Physics:Space travel under constant acceleration
Space travel under constant acceleration is a hypothetical method of space travel that involves the use of a propulsion system that generates a constant acceleration rather than the short, impulsive thrusts produced by traditional chemical rockets. For the first half of the journey the propulsion system would constantly accelerate the spacecraft toward its destination, and for the second half of the journey it would constantly decelerate the spaceship.[1] Constant acceleration could be used to achieve relativistic speeds,[2][3][4] making it a potential means of achieving human interstellar travel. This mode of travel has yet to be used in practice.
Constant-acceleration drives
Constant acceleration has two main advantages:
- It is the fastest form of interplanetary and interstellar travel.
- It creates its own artificial gravity, potentially sparing passengers from the effects of microgravity.
Constant thrust versus constant acceleration
Constant-thrust and constant-acceleration trajectories both involve a spacecraft firing its engine continuously. In a constant-thrust trajectory,[5] the vehicle's acceleration increases during thrusting period, since the use of fuel decreases the vehicle mass. If, instead of constant thrust, the vehicle has constant acceleration, the engine thrust decreases during the journey.
The spacecraft must flip its orientation halfway through the journey and decelerate the rest of the way, if it is required to rendezvous with its destination (as opposed to a flyby).
Interstellar travel

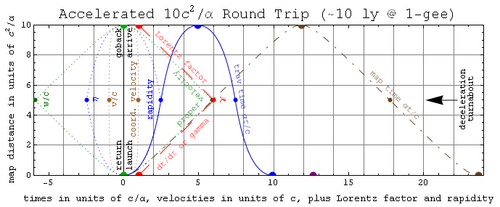
A spaceship using significant constant acceleration will approach the speed of light over interstellar distances, so special relativity effects including time dilation (the difference in time flow between ship time and local time) become important.[7]
Expressions for covered distance and elapsed time
The distance traveled, under constant proper acceleration, from the point of view of Earth as a function of the traveler's time is expressed by the coordinate distance x as a function of proper time τ at constant proper acceleration a. It is given by:[8][9]
- [math]\displaystyle{ x(\tau) = \frac{c^2}{a} \left(\cosh \frac{a \ \tau}{c} -1 \right) , }[/math]
where c is the speed of light.
Under the same circumstances, the time elapsed on Earth (the coordinate time) as a function of the traveler's time is given by:
- [math]\displaystyle{ t(\tau) = \frac{c}{a} \sinh \frac{a \ \tau}{c} . }[/math]
Feasibility
A limitation of constant acceleration is adequate fuel. Constant acceleration is only feasible with the development of fuels with a much higher specific impulse than presently available.
There are two broad approaches to higher specific impulse propulsion:
- Higher efficiency fuel (the motor ship approach). Two possibilities for the motor ship approach are nuclear and matter–antimatter based fuels.
- Drawing propulsion energy from the environment as the ship passes through it (the sailing ship approach). One hypothetical sailing ship approach is discovering something equivalent to the parallelogram of force between wind and water which allows sails to propel a sailing ship.
Picking up fuel along the way — the ramjet approach — will lose efficiency as the space craft's speed increases relative to the planetary reference. This happens because the fuel must be accelerated to the spaceship's velocity before its energy can be extracted, and that will cut the fuel efficiency dramatically.
A related issue is drag. If the near-light-speed space craft is interacting with matter that is moving slowly in the planetary reference frame, this will cause drag which will bleed off a portion of the engine's acceleration.
A second big issue facing ships using constant acceleration for interstellar travel is colliding with matter and radiation while en route. In mid-journey any such impact will be at near light speed, so the result will be dramatic.
Interstellar traveling speeds
If a space ship is using constant acceleration over interstellar distances, it will approach the speed of light for the middle part of its journey when viewed from the planetary frame of reference. This means that the effects of relativity will become important. The most important effect is that time will appear to pass at different rates in the ship frame and the planetary frame, and this means that the ship's speed and journey time will appear different in the two frames.
Planetary reference frame
From the planetary frame of reference, the ship's speed will appear to be limited by the speed of light — it can approach the speed of light, but never reach it. If a ship is using 1 g constant acceleration, it will appear to get near the speed of light in about a year, and have traveled about half a light year in distance. For the middle of the journey the ship's speed will be roughly the speed of light, and it will slow down again to zero over a year at the end of the journey.
As a rule of thumb, for a constant acceleration at 1 g (Earth gravity), the journey time, as measured on Earth, will be the distance in light years to the destination, plus 1 year. This rule of thumb will give answers that are slightly shorter than the exact calculated answer, but reasonably accurate.
Ship reference frame
From the frame of reference of those on the ship the acceleration will not change as the journey goes on. Instead the planetary reference frame will look more and more relativistic. This means that for voyagers on the ship the journey will appear to be much shorter than what planetary observers see.
At a constant acceleration of 1 g, a rocket could travel the diameter of our galaxy in about 12 years ship time, and about 113,000 years planetary time. If the last half of the trip involves deceleration at 1 g, the trip would take about 24 years. If the trip is merely to the nearest star, with deceleration the last half of the way, it would take 3.6 years.[10]
In fiction
The spacecraft of George O. Smith's Venus Equilateral stories are all constant acceleration ships. Normal acceleration is 1 g, but in "The External Triangle" it is mentioned that accelerations of up to 5 g are possible if the crew is drugged with gravanol[11] to counteract the effects of the g-load.
"Sky Lift" is a science fiction short story by Robert A. Heinlein, first published 1953. In the story, a torchship pilot lights out from Earth orbit to Pluto on a mission to deliver a cure to a plague ravaging a research station.[12]
Tau Zero, a hard science fiction novel by Poul Anderson, has a spaceship using a constant acceleration drive.
Spacecraft in Joe Haldeman's 1974 novel The Forever War make extensive use of constant acceleration; they require elaborate safety equipment to keep their occupants alive at high acceleration (up to 25 g), and accelerate at 1 g even when "at rest" to provide humans with a comfortable level of gravity.
In the Known Space universe, constructed by Larry Niven, Earth uses constant acceleration drives in the form of Bussard ramjets to help colonize the nearest planetary systems. In the non-known space novel A World Out of Time, Jerome Branch Corbell (for himself), "takes" a ramjet to the Galactic Center and back in 150 years ships time (most of it in cold sleep), but 3 million years passes on Earth.
In The Sparrow, by Mary Doria Russell, interstellar travel is achieved by converting a small asteroid into a constant acceleration spacecraft. Force is applied by ion engines fed with material mined from the asteroid itself.
In the Revelation Space series by Alastair Reynolds, interstellar commerce depends upon "lighthugger" starships which can accelerate indefinitely at 1 g, with superseded antimatter powered constant acceleration drives. The effects of relativistic travel are an important plot point in several stories, informing the psychologies and politics of the lighthuggers' "ultranaut" crews for example.
In the novel 2061: Odyssey Three by Arthur C. Clarke, the spaceship Universe, using a muon-catalyzed fusion rocket, is capable of constant acceleration at 0.2 g under full thrust. Clarke's novel "Imperial Earth" features an "asymptotic drive", which utilises a microscopic black hole and hydrogen propellant, to achieve a similar acceleration travelling from Titan to Earth.
The UET and Hidden Worlds spaceships of F.M. Busby's Rissa Kerguelen saga utilize a constant acceleration drive that can accelerate at 1 g or even a little more.
Ships in the Expanse series by James S. A. Corey make use of constant acceleration drives, which also provide artificial gravity for the occupants.
In The Martian, by Andy Weir, the spaceship Hermes uses a constant thrust ion engine to transport astronauts between Earth and Mars. In Project Hail Mary, also by Weir, the protagonist's spaceship uses a constant 1.5 g acceleration spin drive to travel between the Solar System, Tau Ceti and 40 Eridani.
Explorers on the Moon, one of the Adventures of Tintin series of comic albums by Hergé, features a manned Moon rocket with an unspecified 'atomic rocket motor'. The ship constantly accelerates from takeoff to provide occupants with consistent gravity, until a mid-way point is reached where the ship is turned around to constantly decelerate towards the Moon.
References
- ↑ Haloupek, William (2013) (in en). Calculations for Science Fiction Writers/Space Travel with Constant Acceleration - The Nonrelativistic Case. Smashwords Edition. ISBN 9781301789078.
- ↑ Joseph Gallant (2012). Doing Physics with Scientific Notebook: A Problem Solving Approach (illustrated ed.). John Wiley & Sons. p. 382. ISBN 978-0-470-66598-5. https://books.google.com/books?id=XWjbyYsBVagC. Extract of page 382
- ↑ Richard F. Tinder (2022). Relativistic Flight Mechanics and Space Travel. Springer Nature. p. 33. ISBN 978-3-031-79297-7. https://books.google.com/books?id=wYFyEAAAQBAJ. Extract of page 33
- ↑ J rgen Freund (2008). Special Relativity for Beginners: A Textbook for Undergraduates. World Scientific. p. 99. ISBN 978-981-277-159-9. https://books.google.com/books?id=J4glh_8RQlMC. Extract of page 99
- ↑ W. E. Moeckel, Trajectories with Constant Tangential Thrust in Central Gravitational Fields, Technical Report R-63, NASA Lewis Research Center, 1960 (accessed 26 March 2014)
 This article incorporates text from this source, which is in the public domain.
This article incorporates text from this source, which is in the public domain.
- ↑ Edwin F. Taylor & John Archibald Wheeler (1966 - first edition only) Spacetime Physics (W.H. Freeman, San Francisco) ISBN:0-7167-0336-X, Chapter 1, Exercise 51, pp. 97–98: "Clock paradox III" (pdf).
- ↑ C. Lagoute and E. Davoust (1995) The interstellar traveler, Am. J. Phys. 63:221–227
- ↑ Koks, Don (2006). Explorations in Mathematical Physics: The Concepts Behind an Elegant Language (illustrated ed.). Springer Science+Business Media. p. 242. ISBN 978-0-387-32793-8. https://books.google.com/books?id=ObMb7l9-9loC. Extract of page 242 (where g=a, c=1 and x0=x(0))
- ↑ Misner, Charles W.; Kip S. Thorne; John Archibald Wheeler (September 1973). Gravitation. San Francisco: W. H. Freeman. Section 6.2. ISBN 0-7167-0344-0.
- ↑ Baez, UCR, "The relativistic rocket"
- ↑ Smith, George O. (1942–1945). Venus Equilateral. Astounding Science Fiction. p. 49. https://archive.org/details/venusequilateral0001smit. Extract of page 49
- ↑ Heinlein, Robert A. (1953). Sky Lift. Greenleaf Publishing Company. p. 164. https://isfdb.org/cgi-bin/title.cgi?62855.
 |