Chemistry:Yield

From HandWiki
Revision as of 00:07, 6 February 2024 by John Stpola (talk | contribs) (add)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Measure of a quantity of moles of a product formed in a chemical reaction


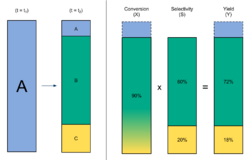
In chemistry, yield, also referred to as reaction yield, is a measure of the quantity of moles of a product formed in relation to the reactant consumed, obtained in a chemical reaction, usually expressed as a percentage.[1] Yield is one of the primary factors that scientists must consider in organic and inorganic chemical synthesis processes.[2] In chemical reaction engineering, "yield", "conversion" and "selectivity" are terms used to describe ratios of how much of a reactant was consumed (conversion), how much desired product was formed (yield) in relation to the undesired product (selectivity), represented as X, Y, and S.

Definitions

Relation between chemical reaction conversion selectivity and yield

In chemical reaction engineering, "yield", "conversion" and "selectivity" are terms used to describe ratios of how much of a reactant has reacted—conversion, how much of a desired product was formed—yield, and how much desired product was formed in ratio to the undesired product—selectivity, represented as X, S, and Y.

According to the Elements of Chemical Reaction Engineering manual, yield refers to the amount of a specific product formed per mole of reactant consumed.[3] In chemistry, mole is used to describe quantities of reactants and products in chemical reactions.

The Compendium of Chemical Terminology defined yield as the "ratio expressing the efficiency of a mass conversion process. The yield coefficient is defined as the amount of cell mass (kg) or product formed (kg,mol)[Notes 1] related to the consumed substrate (carbon or nitrogen source or oxygen in kg or moles) or to the intracellular ATP production (moles)."[4][5]:168

In the section "Calculations of yields in the monitoring of reactions" in the 1996 4th edition of Vogel's Textbook of Practical Organic Chemistry (1978), the authors write that, "theoretical yield in an organic reaction is the weight of product which would be obtained if the reaction has proceeded to completion according to the chemical equation. The yield is the weight of the pure product which is isolated from the reaction."[1]:33 [Notes 2] In 'the 1996 edition of Vogel's Textbook, percentage yield is expressed as,[1]:33[Notes 3]

[math]\displaystyle{ \mbox{percent yield} = \frac{\mbox{weight of product}}{\mbox{theoretical yield}} \times 100 }[/math]

According to the 1996 edition of Vogel's Textbook, yields close to 100% are called quantitative, yields above 90% are called excellent, yields above 80% are very good, yields above 70% are good, yields above 50% are fair, and yields below 40% are called poor.[1]:33 In their 2002 publication, Petrucci, Harwood, and Herring wrote that Vogel's Textbook names were arbitrary, and not universally accepted, and depending on the nature of the reaction in question, these expectations may be unrealistically high. Yields may appear to be 100% or above when products are impure, as the measured weight of the product will include the weight of any impurities.[6]:125

In their 2016 laboratory manual, Experimental Organic Chemistry, the authors described the "reaction yield" or "absolute yield" of a chemical reaction as the "amount of pure and dry product yielded in a reaction".[7] They wrote that knowing the stoichiometry of a chemical reaction—the numbers and types of atoms in the reactants and products, in a balanced equation "make it possible to compare different elements through stoichiometric factors."[7] Ratios obtained by these quantitative relationships are useful in data analysis.[7]

Theoretical, actual, and percent yields

The percent yield is a comparison between the actual yield—which is the weight of the intended product of a chemical reaction in a laboratory setting—and the theoretical yield—the measurement of pure intended isolated product, based on the chemical equation of a flawless chemical reaction,[1] and is defined as,

[math]\displaystyle{ \mbox{percent yield} = \frac{\mbox{actual yield}}{\mbox{theoretical yield}} \times 100 }[/math]

The ideal relationship between products and reactants in a chemical reaction can be obtained by using a chemical reaction equation. Stoichiometry is used to run calculations about chemical reactions, for example, the stoichiometric mole ratio between reactants and products. The stoichiometry of a chemical reaction is based on chemical formulas and equations that provide the quantitative relation between the number of moles of various products and reactants, including yields.[8] Stoichiometric equations are used to determine the limiting reagent or reactant—the reactant that is completely consumed in a reaction. The limiting reagent determines the theoretical yield—the relative quantity of moles of reactants and the product formed in a chemical reaction. Other reactants are said to be present in excess. The actual yield—the quantity physically obtained from a chemical reaction conducted in a laboratory—is often less than the theoretical yield.[8] The theoretical yield is what would be obtained if all of the limiting reagent reacted to give the product in question. A more accurate yield is measured based on how much product was actually produced versus how much could be produced. The ratio of the theoretical yield and the actual yield results in a percent yield.[8]

When more than one reactant participates in a reaction, the yield is usually calculated based on the amount of the limiting reactant, whose amount is less than stoichiometrically equivalent (or just equivalent) to the amounts of all other reactants present. Other reagents present in amounts greater than required to react with all the limiting reagent present are considered excess. As a result, the yield should not be automatically taken as a measure for reaction efficiency.[citation needed]

In their 1992 publication General Chemistry, Whitten, Gailey, and Davis described the theoretical yield as the amount predicted by a stoichiometric calculation based on the number of moles of all reactants present. This calculation assumes that only one reaction occurs and that the limiting reactant reacts completely.[9]

According to Whitten, the actual yield is always smaller (the percent yield is less than 100%), often very much so, for several reasons.[9]:95 As a result, many reactions are incomplete and the reactants are not completely converted to products. If a reverse reaction occurs, the final state contains both reactants and products in a state of chemical equilibrium. Two or more reactions may occur simultaneously, so that some reactant is converted to undesired side products. Losses occur in the separation and purification of the desired product from the reaction mixture. Impurities are present in the starting material which do not react to give desired product.[9]

Example

This is an example of an esterification reaction where one molecule acetic acid (also called ethanoic acid) reacts with one molecule ethanol, yielding one molecule ethyl acetate (a bimolecular second-order reaction of the type A + B → C):

120 g acetic acid (60 g/mol, 2.0 mol) was reacted with 230 g ethanol (46 g/mol, 5.0 mol), yielding 132 g ethyl acetate (88 g/mol, 1.5 mol). The yield was 75%.
  1. The molar amount of the reactants is calculated from the weights (acetic acid: 120 g ÷ 60 g/mol = 2.0 mol; ethanol: 230 g ÷ 46 g/mol = 5.0 mol).
  2. Ethanol is used in a 2.5-fold excess (5.0 mol ÷ 2.0 mol).
  3. The theoretical molar yield is 2.0 mol (the molar amount of the limiting compound, acetic acid).
  4. The molar yield of the product is calculated from its weight (132 g ÷ 88 g/mol = 1.5 mol).
  5. The % yield is calculated from the actual molar yield and the theoretical molar yield (1.5 mol ÷ 2.0 mol × 100% = 75%).[citation needed]

Purification of products

In his 2016 Handbook of Synthetic Organic Chemistry, Michael Pirrung wrote that yield is one of the primary factors synthetic chemists must consider in evaluating a synthetic method or a particular transformation in "multistep syntheses."[10]:163 He wrote that a yield based on recovered starting material (BRSM) or (BORSM) does not provide the theoretical yield or the "100% of the amount of product calculated", that is necessary in order to take the next step in the multistep systhesis.:163

Purification steps always lower the yield, through losses incurred during the transfer of material between reaction vessels and purification apparatus or imperfect separation of the product from impurities, which may necessitate the discarding of fractions deemed insufficiently pure. The yield of the product measured after purification (typically to >95% spectroscopic purity, or to sufficient purity to pass combustion analysis) is called the isolated yield of the reaction.[citation needed]

Internal standard yield

Yields can also be calculated by measuring the amount of product formed (typically in the crude, unpurified reaction mixture) relative to a known amount of an added internal standard, using techniques like Gas chromatography (GC), High-performance liquid chromatography, or Nuclear magnetic resonance spectroscopy (NMR spectroscopy) or magnetic resonance spectroscopy (MRS).[citation needed] A yield determined using this approach is known as an internal standard yield. Yields are typically obtained in this manner to accurately determine the quantity of product produced by a reaction, irrespective of potential isolation problems. Additionally, they can be useful when isolation of the product is challenging or tedious, or when the rapid determination of an approximate yield is desired. Unless otherwise indicated, yields reported in the synthetic organic and inorganic chemistry literature refer to isolated yields, which better reflect the amount of pure product one is likely to obtain under the reported conditions, upon repeating the experimental procedure.[citation needed]

Reporting of yields

In their 2010 Synlett article, Martina Wernerova and organic chemist, Tomáš Hudlický, raised concerns about inaccurate reporting of yields, and offered solutions—including the proper characterization of compounds.[11] After performing careful control experiments, Wernerova and Hudlický said that each physical manipulation (including extraction/washing, drying over desiccant, filtration, and column chromatography) results in a loss of yield of about 2%. Thus, isolated yields measured after standard aqueous workup and chromatographic purification should seldom exceed 94%.[11] They called this phenomenon "yield inflation" and said that yield inflation had gradually crept upward in recent decades in chemistry literature. They attributed yield inflation to careless measurement of yield on reactions conducted on small scale, wishful thinking and a desire to report higher numbers for publication purposes.[11] Hudlický's 2020 article published in Angewandte Chemie—since retracted—honored and echoed Dieter Seebach's often-cited 1990 thirty-year review of organic synthesis, which had also been published in Angewandte Chemie.[12] In his 2020 Angewandte Chemie 30-year review, Hudlický said that the suggestions that he and Wernerova had made in their 2010 Synlett article, were "ignored by the editorial boards of organic journals, and by most referees."[13]

See also

Notes

  1. ↑ The use of kilogram-mole (kg-mol or g-mol)—the number of entities in 12 kg of 12C was replaced with the use of the kilomole (kmol) in the late 20th century. The kilomole is numerically identical to the kilogram-mole. The name and symbol adopt the SI convention for standard multiples of metric units—kmol means 1000 mol.
  2. ↑ The chemist, Arthur Irving Vogel (1905 – 1966) was the author of textbooks including the Textbook of Qualitative Chemical Analysis (1937), the Textbook of Quantitative Chemical Analysis (1939), and the Practical Organic Chemistry (1948).
  3. ↑ In the section "Calculations of yields in the monitoring of reactions" Vogel's Textbook, the authors write that most reactions published in chemical literature provide the molar concentrations of a reagent in solution as well as the quantities of reactants and the weights in grams or milligrams(1996:33)

Further reading

  • Whitten, Kenneth W.; Davis, Raymond E; Peck, M. Larry (2002). General chemistry. Fort Worth: Thomson Learning. ISBN 978-0-03-021017-4. 
  • Whitten, Kenneth W; Gailey, Kenneth D (1981). General chemistry. Philadelphia: Saunders College Pub.. ISBN 978-0-03-057866-3. 
  • Petrucci, Ralph H.; Herring, F. Geoffrey; Madura, Jeffry; Bissonnette, Carey; Pearson (2017). General chemistry: principles and modern applications. Toronto: Pearson. ISBN 978-0-13-293128-1. 
  • Vogel, Arthur Israel; Furniss, B. S; Tatchell, Austin Robert (1978). Vogel's Textbook of practical organic chemistry. New York: Longman. ISBN 978-0-582-44250-4. 

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 Vogel, Arthur Irving (1996). Vogel's Textbook of Practical Organic Chemistry (5 ed.). Prentice Hall. ISBN 978-0-582-46236-6. https://fac.ksu.edu.sa/sites/default/files/vogel_-_practical_organic_chemistry_5th_edition.pdf. Retrieved June 25, 2020. 
  2. ↑ Cornforth, JW (February 1, 1993). "The Trouble With Synthesis". Australian Journal of Chemistry 46 (2): 157–170. doi:10.1071/ch9930157. 
  3. ↑ Fogler, H. Scott (August 23, 2005). Elements of Chemical Reaction Engineering (4 ed.). Prentice Hall. pp. 1120. 
  4. ↑ Glossary for chemists of terms used in biotechnology. Compendium of Chemical Terminology the "Gold Book" (2 ed.). Oxford: Blackwell Scientific Publications. 1997. doi:10.1351/goldbook. ISBN 0-9678550-9-8. https://goldbook.iupac.org/terms/view/Y06724.  S. J. Chalk. Online version (2019-). Last revised February 24, 2014
  5. ↑ PAC, 1992, 64, 143. (Glossary for chemists of terms used in biotechnology (IUPAC Recommendations 1992)) Compendium of Chemical Terminology
  6. ↑ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General chemistry: principles and modern applications (8th ed.). Upper Saddle River, N.J: Prentice Hall. p. 125. ISBN 978-0-13-014329-7. OCLC 46872308. https://archive.org/details/generalchemistry00hill. 
  7. ↑ 7.0 7.1 7.2 Isac-García, Joaquín; Dobado, José A.; Calvo-Flores, Francisco G.; Martínez-Garcí, Henar (2016). Experimental Organic Chemistry (1 ed.). Academic Press. pp. 500. ISBN 9780128038932. https://www.elsevier.com/books/experimental-organic-chemistry/isac-garcia/978-0-12-803893-2. Retrieved June 25, 2020. 
  8. ↑ 8.0 8.1 8.2 Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey; Madura, Jeffry D. (2007). General Chemistry (9 ed.). New Jersey: Pearson Prentice Hall. 
  9. ↑ 9.0 9.1 9.2 Whitten, Kenneth W.; Gailey, K.D.; Davis, Raymond E. (1992). General chemistry (4 ed.). Saunders College Publishing. ISBN 978-0-03-072373-5. 
  10. ↑ Pirrung, Michael C. (August 30, 2016). Handbook of Synthetic Organic Chemistry. Academic Press. ISBN 978-0-12-809504-1. 
  11. ↑ 11.0 11.1 11.2 Wernerova, Martina; Hudlicky, Tomas (November 2010). "On the Practical Limits of Determining Isolated Product Yields and Ratios of Stereoisomers: Reflections, Analysis, and Redemption" (in en). Synlett 2010 (18): 2701–2707. doi:10.1055/s-0030-1259018. ISSN 1437-2096. 
  12. ↑ Seebach, Dieter (1990). "Organic Synthesis—Where now?". Angewandte Chemie 29 (11): 1320–1367. doi:10.1002/anie.199013201. ISSN 1521-3773. 
  13. ↑ Hudlicky, Tomas (June 4, 2020). ""Organic synthesis—Where now?" is thirty years old. A reflection on the current state of affairs". Angewandte Chemie. Opinion 59 (31): 12576. doi:10.1002/anie.202006717. PMID 32497328.  Retracted.




Retrieved from "https://handwiki.org/wiki/index.php?title=Chemistry:Yield&oldid=3329849"