Thickness (graph theory)
In graph theory, the thickness of a graph G is the minimum number of planar graphs into which the edges of G can be partitioned. That is, if there exists a collection of k planar graphs, all having the same set of vertices, such that the union of these planar graphs is G, then the thickness of G is at most k.[1]Cite error: Closing </ref> missing for <ref> tag and on a related 1962 conjecture of Frank Harary: For any graph on 9 points, either itself or its complementary graph is non-planar. The problem is equivalent to determining whether the complete graph K9 is biplanar (it is not, and the conjecture is true).[2] A comprehensive[3] survey on the state of the arts of the topic as of 1998 was written by Petra Mutzel, Thomas Odenthal and Mark Scharbrodt.[4]
Specific graphs
The thickness of the complete graph on n vertices, Kn, is
- [math]\displaystyle{ \left \lfloor \frac{n+7}{6} \right\rfloor, }[/math]
except when n = 9, 10 for which the thickness is three.[5][6]
With some exceptions, the thickness of a complete bipartite graph Ka,b is generally:[7][8]
- [math]\displaystyle{ \left \lceil \frac{ab}{2(a+b-2)} \right \rceil. }[/math]
Properties
Every forest is planar, and every planar graph can be partitioned into at most three forests. Therefore, the thickness of any graph G is at most equal to the arboricity of the same graph (the minimum number of forests into which it can be partitioned) and at least equal to the arboricity divided by three.[4][9]
The graphs of maximum degree [math]\displaystyle{ d }[/math] have thickness at most [math]\displaystyle{ \lceil d/2\rceil }[/math].[10] This cannot be improved: for a [math]\displaystyle{ d }[/math]-regular graph with girth at least [math]\displaystyle{ 2d }[/math], the high girth forces any planar subgraph to be sparse, causing its thickness to be exactly [math]\displaystyle{ \lceil d/2\rceil }[/math].[11]
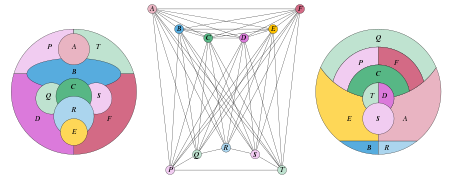
Graphs of thickness [math]\displaystyle{ t }[/math] with [math]\displaystyle{ n }[/math] vertices have at most [math]\displaystyle{ t(3n-6) }[/math] edges. Because this gives them average degree less than [math]\displaystyle{ 6t }[/math], their degeneracy is at most [math]\displaystyle{ 6t-1 }[/math] and their chromatic number is at most [math]\displaystyle{ 6t }[/math]. Here, the degeneracy can be defined as the maximum, over subgraphs of the given graph, of the minimum degree within the subgraph. In the other direction, if a graph has degeneracy [math]\displaystyle{ D }[/math] then its arboricity and thickness are at most [math]\displaystyle{ D }[/math]. One can find an ordering of the vertices of the graph in which each vertex has at most [math]\displaystyle{ D }[/math] neighbors that come later than it in the ordering, and assigning these edges to [math]\displaystyle{ D }[/math] distinct subgraphs produces a partition of the graph into [math]\displaystyle{ D }[/math] trees, which are planar graphs.
Even in the case [math]\displaystyle{ t=2 }[/math], the precise value of the chromatic number is unknown; this is Gerhard Ringel's Earth–Moon problem. An example of Thom Sulanke shows that, for [math]\displaystyle{ t=2 }[/math], at least 9 colors are needed.[12]
Related problems
Thickness is closely related to the problem of simultaneous embedding.Cite error: Closing </ref> missing for <ref> tag
Computational complexity
It is NP-hard to compute the thickness of a given graph, and NP-complete to test whether the thickness is at most two.[13] However, the connection to arboricity allows the thickness to be approximated to within an approximation ratio of 3 in polynomial time.
References
- ↑ Tutte, W. T. (1963), "The thickness of a graph", Indag. Math. 66: 567–577, doi:10.1016/S1385-7258(63)50055-9.
- ↑ Mäkinen, Erkki; Poranen, Timo (2012), "An annotated bibliography on the thickness, outerthickness, and arboricity of a graph", Missouri J. Math. Sci. 24 (1): 76–87, doi:10.35834/mjms/1337950501, http://projecteuclid.org/euclid.mjms/1337950501
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedduncan2009 - ↑ 4.0 4.1 Cite error: Invalid
<ref>tag; no text was provided for refs namedmos - ↑ (Mutzel Odenthal), Theorem 3.2.
- ↑ Alekseev, V. B.; Gončakov, V. S. (1976), "The thickness of an arbitrary complete graph", Mat. Sb., New Series 101 (143): 212–230, doi:10.1070/SM1976v030n02ABEH002267, Bibcode: 1976SbMat..30..187A.
- ↑ (Mutzel Odenthal), Theorem 3.4.
- ↑ Beineke, Lowell W.; Harary, Frank; Moon, John W. (1964), "On the thickness of the complete bipartite graph", Proc. Cambridge Philos. Soc. 60 (1): 1–5, doi:10.1017/s0305004100037385, Bibcode: 1964PCPS...60....1B.
- ↑ Dean, Alice M.; Hutchinson, Joan P.; Scheinerman, Edward R. (1991), "On the thickness and arboricity of a graph", Journal of Combinatorial Theory, Series B 52 (1): 147–151, doi:10.1016/0095-8956(91)90100-X.
- ↑ Halton, John H. (1991), "On the thickness of graphs of given degree", Information Sciences 54 (3): 219–238, doi:10.1016/0020-0255(91)90052-V
- ↑ Sýkora, Ondrej; Székely, László A.; Vrt'o, Imrich (2004), "A note on Halton's conjecture", Information Sciences 164 (1–4): 61–64, doi:10.1016/j.ins.2003.06.008
- ↑ "To the Moon and beyond", Graph Theory: Favorite Conjectures and Open Problems, II, Problem Books in Mathematics, Springer International Publishing, 2018, pp. 115–133, doi:10.1007/978-3-319-97686-0_11
- ↑ Mansfield, Anthony (1983), "Determining the thickness of graphs is NP-hard", Mathematical Proceedings of the Cambridge Philosophical Society 93 (1): 9–23, doi:10.1017/S030500410006028X, Bibcode: 1983MPCPS..93....9M.
 |

