Earth–Moon problem

Short description: Unsolved problem on graph coloring

Unsolved problem in mathematics: How many colors are needed to color biplanar graphs? (more unsolved problems in mathematics)

The Earth–Moon problem is an unsolved problem on graph coloring in mathematics. It is an extension of the planar map coloring problem (solved by the four color theorem), and was posed by Gerhard Ringel in 1959. In mathematical terms, it seeks the chromatic number of biplanar graphs. It is known that this number is at least 9 and at most 12.

Formulation

In the map coloring problem, a collection of simply connected regions in the Euclidean plane or a topologically equivalent space, such as countries on the surface of the Earth, are to be colored so that, when two regions have a nonzero length of boundary, they have different colors. It can be transformed into a graph coloring problem by making a vertex for each region and an edge for each two neighboring regions, producing a planar graph whose vertices are to be colored. According to the four color theorem, it is always possible to do so using at most four different colors, no matter how many regions are given.

Instead, in the Earth–Moon problem, each country on the Earth has a corresponding colony on the surface of the Moon, that must be given the same color. These colonies may have borders that are completely different from the arrangement of the borders on the Earth. The countries must be colored, using the same color for each country and its colony, so that when two countries share a border either on the Earth or on the Moon they are given different colors. Ringel's problem asks: how many colors are needed to guarantee that the countries can all be colored, no matter how their boundaries are arranged?

Again, one can phrase the same question equivalently as one in graph theory, with a single vertex for each pair of a country and its colony, and an edge for each adjacency between countries or colonies. The graphs that result in this version of the problem are biplanar graphs, or equivalently the graphs of thickness two: their edges can be partitioned into two subsets (the Earth adjacencies and the Moon adjacencies) such that the corresponding two subgraphs are both planar. In mathematical terms, Ringel's problem asks for the maximum chromatic number of biplanar graphs.

Bounds

A biplanar graph on [math]\displaystyle{ n }[/math] vertices has at most [math]\displaystyle{ 6n-12 }[/math] edges (double the number that a planar graph can have), from which it follows that it has at least one vertex with only 11 neighbors. Removing this vertex, coloring the remaining graph recursively, and then using the smallest-numbered unused color for the removed vertex leads to a coloring with at most 12 colors; this is the greedy coloring for a degeneracy ordering of the graph. Therefore, biplanar graphs require at most 12 colors.

Sulanke's nine-color Earth–Moon map (left and right), with adjacencies described by the join of a 6-vertex complete graph and 5-vertex cycle graph (center)

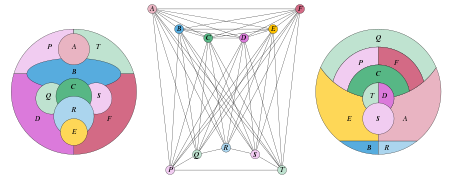
An example of a biplanar graph requiring 9 colors can be constructed as the join of a 6-vertex complete graph and a 5-vertex cycle graph. This means that these two subgraphs are connected by all possible edges from one subgraph to the other. The resulting graph has 11 vertices, and requires 6 colors for the complete subgraph and 3 colors for the cycle subgraph, giving 9 colors overall. This construction, by Thom Sulanke in 1974, disproved a conjecture by Ringel that 8 colors would always suffice. Subsequently, infinitely many examples of biplanar 9-critical graphs (minimal graphs that require nine colors) have been constructed.

Despite a lack of further progress on the problem, in 2018 Ellen Gethner conjectured that the correct number of colors for this problem is 11. She suggests several candidates for 10-chromatic biplanar graphs, including the graph [math]\displaystyle{ C_7\boxtimes K_4 }[/math] obtained as the strong product of a cycle graph with a clique, and the graph obtained by removing any vertex from [math]\displaystyle{ C_5\boxtimes K_4 }[/math]. These graphs can be shown to require 10 colors, because they have no independent set large enough to be the largest color class in a coloring with fewer colors. Additionally, they meet the bounds on the number of edges a biplanar graph can have. However, a representation of them as biplanar graphs (or Earth–Moon maps) remains elusive.

Application

One application of colorings of biplanar graphs involves testing printed circuit boards for short circuits. The electrical conductors within these boards include crossings, but their adjacencies can be assumed to form a biplanar graph. After coloring this graph, short circuits between adjacent conductors can be detected by adding extra circuitry to connect all conductors with the same colors to each other and testing for connections between pairs of different colors. With some care, this idea can be used to reduce the number of tests needed per circuit to only four.

Generalizations

Various generalizations of the problem have also been considered, including versions of the problem with more than two planets or with countries that can have more than one region per planet. In particular, graphs of thickness [math]\displaystyle{ t\ge 3 }[/math] (representing maps with more than two planets but only one region per planet), more precise (although still incomplete) results are known. For these graphs, the chromatic number is at most [math]\displaystyle{ 6t }[/math] by the same degeneracy argument used in the Earth–Moon problem. As well, for [math]\displaystyle{ t\ge 3 }[/math], a complete graph with [math]\displaystyle{ 6t-2 }[/math] vertices has thickness [math]\displaystyle{ t }[/math], showing some of these graphs require [math]\displaystyle{ 6t-2 }[/math] colors. Thus, in this case, the upper and lower bounds are within two colors of each other.

External links

• Weisstein, Eric W.. "Earth-Moon Problem". http://mathworld.wolfram.com/Earth-MoonProblem.html. 
• "Earth-Moon Problem", Open Problem Garden, http://www.openproblemgarden.org/op/earth_moon_problem