Hopf algebroid

In mathematics, in the theory of Hopf algebras, a Hopf algebroid is a generalisation of weak Hopf algebras, certain skew Hopf algebras and commutative Hopf k-algebroids. If k is a field, a commutative k-algebroid is a cogroupoid object in the category of k-algebras; the category of such is hence dual to the category of groupoid k-schemes. This commutative version has been used in 1970-s in algebraic geometry and stable homotopy theory. The generalization of Hopf algebroids and its main part of the structure, associative bialgebroids, to the noncommutative base algebra was introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry (later shown equivalent in nontrivial way to a construction of Takeuchi from the 1970s and another by Xu around the year 2000). They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra H^L. The antipode axioms have been changed by G. Böhm and K. Szlachányi (J. Algebra) in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra extensions.

Definition

The main motivation behind of the definition of a Hopf algebroid^pg301-302 is its a commutative algebraic representation of an algebraic stack which can be presented as affine schemes. More generally, Hopf algebroids encode the data of presheaves of groupoids on the category [math]\displaystyle{ \text{Aff} }[/math] of affine schemes. That is, if we have a groupoid object of affine schemes

[math]\displaystyle{ s,t:X_1 \rightrightarrows X_0 }[/math]

with an identity map [math]\displaystyle{ \iota: X_0 \to X_1 }[/math] giving an embedding of objects into the arrows, we can take as our definition of a Hopf algebroid as the dual objects in commutative rings [math]\displaystyle{ \text{CRing} }[/math] which encodes this structure. Note that this process is essentially an application of the Yoneda lemma to the definition of the groupoid schemes in the category [math]\displaystyle{ \text{Aff} }[/math] of affine schemes. Since we may want to fix a base ring, we will instead consider the category [math]\displaystyle{ \text{CRing}_k }[/math] of commutative [math]\displaystyle{ k }[/math]-algebras.

Scheme-theoretic definition

Algebraic objects in the definition

A Hopf algebroid over a commutative ring [math]\displaystyle{ k }[/math] is a pair of [math]\displaystyle{ k }[/math]-algebras [math]\displaystyle{ (A,\Gamma) }[/math] in [math]\displaystyle{ \text{CRing}_k }[/math] such that their functor of points

[math]\displaystyle{ \text{Hom}_k(\Gamma,-) \rightrightarrows \text{Hom}_k(A,-) }[/math]

encodes a groupoid in [math]\displaystyle{ \text{Aff} }[/math]. If we fix [math]\displaystyle{ B }[/math] as some object in [math]\displaystyle{ \text{CRing}_k }[/math], then [math]\displaystyle{ \text{Hom}_k(A,B) }[/math] is the set of objects in the groupoid and [math]\displaystyle{ \text{Hom}_k(\Gamma,B) }[/math] is the set of arrows. This translates to having maps

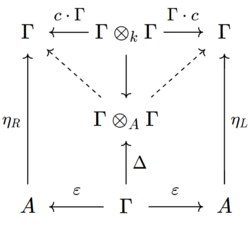
[math]\displaystyle{ \begin{align} \eta_L&:A \to \Gamma & \text{ left unit/ source map} \\ \eta_R&:A \to \Gamma & \text{ right unit/ target map} \\ \Delta&:\Gamma \to \Gamma\otimes_A\Gamma & \text{ coproduct/ composition map} \\ \varepsilon&:\Gamma \to A & \text{ counit/ identity map } \\ c&:\Gamma \to \Gamma & \text{ conjugation/ inverse map} \end{align} }[/math]

where the text on the left hand side of the slash is the traditional word used for the map of algebras giving the Hopf algebroid structure and the text on the right hand side of the slash is what corresponding structure on the groupoid

[math]\displaystyle{ \text{Hom}_k(\Gamma,-) \rightrightarrows \text{Hom}_k(A,-) }[/math]

these maps correspond to, meaning their dual maps from the Yoneda embedding gives the structure of a groupoid. For example,

[math]\displaystyle{ \eta_L^*: {\text{Hom}}_{k}(\Gamma ,-)\rightarrow {\text{Hom}}_{k}(A,-) }[/math]

corresponds to the source map [math]\displaystyle{ s }[/math].

Axioms these maps must satisfy

In addition to these maps, they satisfy a host of axioms dual to the axioms of a groupoid. Note we will fix [math]\displaystyle{ B }[/math] as some object in [math]\displaystyle{ \text{CRing}_k }[/math] giving

1. [math]\displaystyle{ \varepsilon \eta_L = \varepsilon \eta_R = \text{Id}_A }[/math], meaning the dual counit map [math]\displaystyle{ \varepsilon^* }[/math] acts as a two-sided identity for the objects in [math]\displaystyle{ \text{Hom}_k(A,B) }[/math]
2. [math]\displaystyle{ (\text{Id}_\Gamma\otimes \varepsilon) \Delta = (\varepsilon \otimes \text{Id}_\Gamma)\Delta = \text{Id}_\Gamma }[/math], meaning composing an arrow with the identity leaves that arrow unchanged
3. [math]\displaystyle{ (\text{Id}_\Gamma\otimes \Delta) \Delta = (\Delta \otimes \text{Id}_\Gamma)\Delta = \text{Id}_\Gamma }[/math] corresponds to the associativity of composition of morphisms
4. [math]\displaystyle{ c\eta_R = \eta_L }[/math] and [math]\displaystyle{ c\eta_L = \eta_R }[/math], translates to inverting a morphism interchanges the source and target
5. [math]\displaystyle{ cc = \text{Id}_\Gamma }[/math], meaning the inverse of the inverse is the original map
6. These exists maps [math]\displaystyle{ \Gamma\otimes_A\Gamma \rightrightarrows \Gamma }[/math] encoding the composition of a morphism with its inverse on either side gives the identity morphism. This can be encoded by the commutative diagram below where the dashed arrows represent the existence of these two arrows

where [math]\displaystyle{ c\cdot \Gamma }[/math] is the map [math]\displaystyle{ c\cdot\Gamma(\gamma_1\otimes \gamma_2) = c(\gamma_1)\gamma_2 }[/math] and [math]\displaystyle{ \Gamma\cdot c(\gamma_1\otimes \gamma_2) = \gamma_1c(\gamma_2) }[/math].

Additional structures

In addition to the standard definition of a Hopf-algebroid, there are also graded commutative Hopf-algebroids which are pairs of graded commutative algebras [math]\displaystyle{ (A,\Gamma) }[/math] with graded commutative structure maps given above.

Also, a graded Hopf algebroid [math]\displaystyle{ (A,\Gamma) }[/math] is said to be connected if the right and left sub [math]\displaystyle{ A }[/math]-modules [math]\displaystyle{ \Gamma_0 \hookrightarrow \Gamma }[/math] are both isomorphic to [math]\displaystyle{ A }[/math]

Another definition

A left Hopf algebroid (H, R) is a left bialgebroid together with an antipode: the bialgebroid (H, R) consists of a total algebra H and a base algebra R and two mappings, an algebra homomorphism s: R → H called a source map, an algebra anti-homomorphism t: R → H called a target map, such that the commutativity condition s(r₁) t(r₂) = t(r₂) s(r₁) is satisfied for all r₁, r₂ ∈ R. The axioms resemble those of a Hopf algebra but are complicated by the possibility that R is a non-commutative algebra or its images under s and t are not in the center of H. In particular a left bialgebroid (H, R) has an R-R-bimodule structure on H which prefers the left side as follows: r₁ ⋅ h ⋅ r₂ = s(r₁) t(r₂) h for all h in H, r₁, r₂ ∈ R. There is a coproduct Δ: H → H ⊗_R H and counit ε: H → R that make (H, R, Δ, ε) an R-coring (with axioms like that of a coalgebra such that all mappings are R-R-bimodule homomorphisms and all tensors over R). Additionally the bialgebroid (H, R) must satisfy Δ(ab) = Δ(a)Δ(b) for all a, b in H, and a condition to make sure this last condition makes sense: every image point Δ(a) satisfies a₍₁₎ t(r) ⊗ a₍₂₎ = a₍₁₎ ⊗ a₍₂₎ s(r) for all r in R. Also Δ(1) = 1 ⊗ 1. The counit is required to satisfy ε(1_H) = 1_R and the condition ε(ab) = ε(as(ε(b))) = ε(at(ε(b))).

The antipode S: H → H is usually taken to be an algebra anti-automorphism satisfying conditions of exchanging the source and target maps and satisfying two axioms like Hopf algebra antipode axioms; see the references in Lu or in Böhm-Szlachányi for a more example-category friendly, though somewhat more complicated, set of axioms for the antipode S. The latter set of axioms depend on the axioms of a right bialgebroid as well, which are a straightforward switching of left to right, s with t, of the axioms for a left bialgebroid given above.

Examples

From algebraic topology

One of the main motivating examples of a Hopf algebroid is the pair [math]\displaystyle{ (\pi_*(E), E_*(E)) }[/math] for a spectrum [math]\displaystyle{ E }[/math]. For example, the Hopf algebroids [math]\displaystyle{ (\pi_*(\text{MU}), \text{MU}_*(\text{MU})) }[/math], [math]\displaystyle{ (\pi_*(\text{BP}), \text{BP}_*(\text{BP})) }[/math], for the spectra representing complex cobordism and Brown-Peterson homology, and truncations of them are widely studied in algebraic topology. This is because of their use in the Adams-Novikov spectral sequence for computing the stable homotopy groups of spheres.

Hopf algebroid corepresenting stack of formal group laws

There is a Hopf-algebroid which corepresents the stack of formal group laws [math]\displaystyle{ \mathcal{M}_{FG} }[/math] which is constructed using algebraic topology. If we let [math]\displaystyle{ \text{MP} }[/math] denote the spectrum

[math]\displaystyle{ \text{MP} = \bigvee_{m \in \mathbb{Z}}\Sigma^{2m}\text{MU} }[/math]

there is a Hopf algebroid

[math]\displaystyle{ \text{MP}_0 \rightrightarrows \text{MP}_0(\text{MP}) }[/math]

corepresenting the stack [math]\displaystyle{ \mathcal{M}_{FG} }[/math]. This means, there is an isomorphism of functors

[math]\displaystyle{ \mathcal{M}_{FG}(-) \cong [\text{MP}_0 \rightrightarrows \text{MP}_0(\text{MP})](-) }[/math]

where the functor on the right sends a commutative ring [math]\displaystyle{ B }[/math] to the groupoid

[math]\displaystyle{ \text{MP}_0(B) \rightrightarrows \text{MP}_0(\text{MP})(B) }[/math]

Other examples

As an example of left bialgebroid, take R to be any algebra over a field k. Let H be its algebra of linear self-mappings. Let s(r) be left multiplication by r on R; let t(r) be right multiplication by r on R. H is a left bialgebroid over R, which may be seen as follows. From the fact that H ⊗_R H ≅ Hom_k(R ⊗ R, R) one may define a coproduct by Δ(f)(r ⊗ u) = f(ru) for each linear transformation f from R to itself and all r, u in R. Coassociativity of the coproduct follows from associativity of the product on R. A counit is given by ε(f) = f(1). The counit axioms of a coring follow from the identity element condition on multiplication in R. The reader will be amused, or at least edified, to check that (H, R) is a left bialgebroid. In case R is an Azumaya algebra, in which case H is isomorphic to R ⊗ R, an antipode comes from transposing tensors, which makes H a Hopf algebroid over R. Another class of examples comes from letting R be the ground field; in this case, the Hopf algebroid (H, R) is a Hopf algebra.

See also

• Cotensor product
• Extension of Hopf algebroids
• Comodule over a Hopf algebroid

Further reading

• Böhm, Gabriella (2005). "An alternative notion of Hopf algebroid". in Caenepeel, Stefaan. Hopf algebras in noncommutative geometry and physics. Proceedings of the conference on Hopf algebras and quantum groups, Brussels, Belgium, May 28–June 1, 2002. Lecture Notes in Pure and Applied Mathematics. 239. New York, NY: Marcel Dekker. pp. 31–53. ISBN 978-0-8247-5759-5. 
• Böhm, Gabriella; Szlachányi, Kornél (2004). "Hopf algebroid symmetry of abstract Frobenius extensions of depth 2". Commun. Algebra 32 (11): 4433–4464. doi:10.1081/AGB-200034171. 
• Jiang-Hua Lu, "Hopf algebroids and quantum groupoids", Int. J. Math. 7, n. 1 (1996) pp. 47–70, https://arxiv.org/abs/q-alg/9505024, http://www.ams.org/mathscinet-getitem?mr=95e:16037, https://dx.doi.org/10.1142/S0129167X96000050