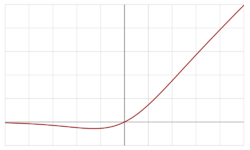
Swish function

Short description: Mathematical activation function in data analysis

The swish function is a mathematical function defined as follows:

The swish function

[math]\displaystyle{ \operatorname{swish}(x) = x \operatorname{sigmoid}(\beta x) = \frac{x}{1+e^{-\beta x}}. }[/math]

where β is either constant or a trainable parameter depending on the model. For β = 1, the function becomes equivalent to the Sigmoid Linear Unit or SiLU, first proposed alongside the GELU in 2016. The SiLU was later rediscovered in 2017 as the Sigmoid-weighted Linear Unit (SiL) function used in reinforcement learning. The SiLU/SiL was then rediscovered as the swish over a year after its initial discovery, originally proposed without the learnable parameter β, so that β implicitly equalled 1. The swish paper was then updated to propose the activation with the learnable parameter β, though researchers usually let β = 1 and do not use the learnable parameter β. For β = 0, the function turns into the scaled linear function f(x) = x/2. With β → ∞, the sigmoid component approaches a 0-1 function pointwise, so swish approaches the ReLU function pointwise. Thus, it can be viewed as a smoothing function which nonlinearly interpolates between a linear function and the ReLU function. This function uses non-monotonicity, and may have influenced the proposal of other activation functions with this property such as Mish.

When considering positive values, Swish is a particular case of sigmoid shrinkage function defined in (see the doubly parameterized sigmoid shrinkage form given by Equation (3) of this reference).

Applications

In 2017, after performing analysis on ImageNet data, researchers from Google indicated that using this function as an activation function in artificial neural networks improves the performance, compared to ReLU and sigmoid functions. It is believed that one reason for the improvement is that the swish function helps alleviate the vanishing gradient problem during backpropagation.