Erasure code

Short description: Code added to allow recovery of lost data

In coding theory, an erasure code is a forward error correction (FEC) code under the assumption of bit erasures (rather than bit errors), which transforms a message of k symbols into a longer message (code word) with n symbols such that the original message can be recovered from a subset of the n symbols. The fraction r = k/n is called the code rate. The fraction k’/k, where k’ denotes the number of symbols required for recovery, is called reception efficiency.

Optimal erasure codes

Optimal erasure codes have the property that any k out of the n code word symbols are sufficient to recover the original message (i.e., they have optimal reception efficiency). Optimal erasure codes are maximum distance separable codes (MDS codes).

Parity check

Parity check is the special case where n = k + 1. From a set of k values [math]\displaystyle{ \{v_i\}_{1\leq i \leq k} }[/math], a checksum is computed and appended to the k source values:

[math]\displaystyle{ v_{k+1}= - \sum_{i=1}^k v_i. }[/math]

The set of k + 1 values [math]\displaystyle{ \{v_i\}_{1\leq i \leq k+1} }[/math] is now consistent with regard to the checksum. If one of these values, [math]\displaystyle{ v_e }[/math], is erased, it can be easily recovered by summing the remaining variables:

[math]\displaystyle{ v_{e}= - \sum_{i=1 ,i \neq e }^{k+1}v_i. }[/math]

Polynomial oversampling

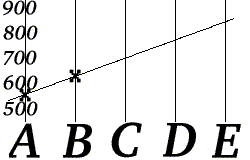
Example: Err-mail (k = 2)

In the simple case where k = 2, redundancy symbols may be created by sampling different points along the line between the two original symbols. This is pictured with a simple example, called err-mail:

Alice wants to send her telephone number (555629) to Bob using err-mail. Err-mail works just like e-mail, except

1. About half of all the mail gets lost.
2. Messages longer than 5 characters are illegal.
3. It is very expensive (similar to air-mail).

Instead of asking Bob to acknowledge the messages she sends, Alice devises the following scheme.

1. She breaks her telephone number up into two parts a = 555, b = 629, and sends 2 messages – "A=555" and "B=629" – to Bob.
2. She constructs a linear function, [math]\displaystyle{ f(i) = a + (b-a)(i-1) }[/math], in this case [math]\displaystyle{ f(i) = 555 + 74(i-1) }[/math], such that [math]\displaystyle{ f(1) = 555 }[/math] and [math]\displaystyle{ f(2) = 629 }[/math].

1. She computes the values f(3), f(4), and f(5), and then transmits three redundant messages: "C=703", "D=777" and "E=851".

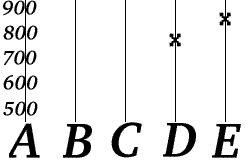
Bob knows that the form of f(k) is [math]\displaystyle{ f(i) = a + (b-a)(i-1) }[/math], where a and b are the two parts of the telephone number. Now suppose Bob receives "D=777" and "E=851".

Bob can reconstruct Alice's phone number by computing the values of a and b from the values (f(4) and f(5)) he has received. Bob can perform this procedure using any two err-mails, so the erasure code in this example has a rate of 40%.

Note that Alice cannot encode her telephone number in just one err-mail, because it contains six characters, and that the maximum length of one err-mail message is five characters. If she sent her phone number in pieces, asking Bob to acknowledge receipt of each piece, at least four messages would have to be sent anyway (two from Alice, and two acknowledgments from Bob). So the erasure code in this example, which requires five messages, is quite economical.

This example is a little bit contrived. For truly generic erasure codes that work over any data set, we would need something other than the f(i) given.

General case

The linear construction above can be generalized to polynomial interpolation. Additionally, points are now computed over a finite field.

First we choose a finite field F with order of at least n, but usually a power of 2. The sender numbers the data symbols from 0 to k − 1 and sends them. He then constructs a (Lagrange) polynomial p(x) of order k such that p(i) is equal to data symbol i. He then sends p(k), ..., p(n − 1). The receiver can now also use polynomial interpolation to recover the lost packets, provided he receives k symbols successfully. If the order of F is less than 2^b, where b is the number of bits in a symbol, then multiple polynomials can be used.

The sender can construct symbols k to n − 1 'on the fly', i.e., distribute the workload evenly between transmission of the symbols. If the receiver wants to do his calculations 'on the fly', he can construct a new polynomial q, such that q(i) = p(i) if symbol i < k was received successfully and q(i) = 0 when symbol i < k was not received. Now let r(i) = p(i) − q(i). Firstly we know that r(i) = 0 if symbol i < k has been received successfully. Secondly, if symbol i ≥ k has been received successfully, then r(i) = p(i) − q(i) can be calculated. So we have enough data points to construct r and evaluate it to find the lost packets. So both the sender and the receiver require O(n (n − k)) operations and only O(n − k) space for operating 'on the fly'.

Real world implementation

This process is implemented by Reed–Solomon codes, with code words constructed over a finite field using a Vandermonde matrix.

Most practical erasure codes are systematic codes -- each one of the original k symbols can be found copied, unencoded, as one of the n message symbols. (Erasure codes that support secret sharing never use a systematic code).

Near-optimal erasure codes

Near-optimal erasure codes require (1 + ε)k symbols to recover the message (where ε>0). Reducing ε can be done at the cost of CPU time. Near-optimal erasure codes trade correction capabilities for computational complexity: practical algorithms can encode and decode with linear time complexity.

Fountain codes (also known as rateless erasure codes) are notable examples of near-optimal erasure codes. They can transform a k symbol message into a practically infinite encoded form, i.e., they can generate an arbitrary amount of redundancy symbols that can all be used for error correction. Receivers can start decoding after they have received slightly more than k encoded symbols.

Regenerating codes address the issue of rebuilding (also called repairing) lost encoded fragments from existing encoded fragments. This issue occurs in distributed storage systems where communication to maintain encoded redundancy is a problem.

Applications of erasure coding in storage systems

Erasure coding is now standard practice for reliable data storage. In particular, various implementations of Reed-Solomon erasure coding are used by Apache Hadoop, the RAID-6 built into Linux, Microsoft Azure, Facebook cold storage, and Backblaze Vaults.

The classical way to recover from failures in storage systems was to use replication. However, replication incurs significant overhead in terms of wasted bytes. Therefore, increasingly large storage systems, such as those used in data centers use erasure-coded storage. The most common form of erasure coding used in storage systems is Reed-Solomon (RS) code, an advanced mathematics formula used to enable regeneration of missing data from pieces of known data, called parity blocks. In a (k, m) RS code, a given set of k data blocks, called "chunks", are encoded into (k + m) chunks. The total set of chunks comprises a stripe. The coding is done such that as long as at least k out of (k + m) chunks are available, one can recover the entire data. This means a (k, m) RS-encoded storage can tolerate up to m failures.

Example: In RS (10, 4) code, which is used in Facebook for their HDFS, 10 MB of user data is divided into ten 1MB blocks. Then, four additional 1 MB parity blocks are created to provide redundancy. This can tolerate up to 4 concurrent failures. The storage overhead here is 14/10 = 1.4X.

In the case of a fully replicated system, the 10 MB of user data will have to be replicated 4 times to tolerate up to 4 concurrent failures. The storage overhead in that case will be 50/10 = 5 times.

This gives an idea of the lower storage overhead of erasure-coded storage compared to full replication and thus the attraction in today's storage systems.

Initially, erasure codes were used to reduce the cost of storing "cold" (rarely-accessed) data efficiently; but erasure codes can also be used to improve performance serving "hot" (more-frequently-accessed) data.

Examples

Here are some examples of implementations of the various codes:

Near optimal erasure codes

• Tornado codes
• Low-density parity-check codes

Near optimal fountain (rateless erasure) codes

• Fountain code
• Online codes
• LT codes
• Raptor codes
• Network Codes
• Triangular codes

Optimal erasure codes

• Parity: used in RAID storage systems.
• Parchive
• Tahoe-LAFS includes zfec
• Reed–Solomon codes
• Erasure Resilient Systematic Code, an MDS code outperforming Reed–Solomon in the maximal number of redundant packets, see RS(4,2) with 2 bits or RS(9,2) with 3 bits
• Regenerating Codes
• any other maximum distance separable code

See also

• Forward error correction codes.
• Secret sharing (differs in that the original secret is encrypted and obscured until the decode quorum is reached)
• Spelling alphabet

External links

• Jerasure is a Free Software library implementing Reed-Solomon and Cauchy erasure code techniques with SIMD optimisations.
• Software FEC in computer communications by Luigi Rizzo describes optimal erasure correction codes
• Feclib is a near optimal extension to Luigi Rizzo's work that uses band matrices. Many parameters can be set, like the size of the width of the band and size of the finite field. It also successfully exploits the large register size of modern CPUs. How it compares to the near optimal codes mentioned above is unknown.
• Coding for Distributed Storage wiki for regenerating codes and rebuilding erasure codes.
• ECIP "Erasure Code Internet Protocol" Developed in 1996, was the first use of FEC "Forward Error correction" on the Internet. It was first used commercially to *stream live video of Sir Arthur C. Clarke in Sri Lanka to UIUC in Indiana.