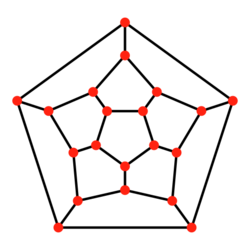
Polyhedral graph
In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.
Characterization
The Schlegel diagram of a convex polyhedron represents its vertices and edges as points and line segments in the Euclidean plane, forming a subdivision of an outer convex polygon into smaller convex polygons (a convex drawing of the graph of the polyhedron). It has no crossings, so every polyhedral graph is also a planar graph. Additionally, by Balinski's theorem, it is a 3-vertex-connected graph.
According to Steinitz's theorem, these two graph-theoretic properties are enough to completely characterize the polyhedral graphs: they are exactly the 3-vertex-connected planar graphs. That is, whenever a graph is both planar and 3-vertex-connected, there exists a polyhedron whose vertices and edges form an isomorphic graph.[1][2] Given such a graph, a representation of it as a subdivision of a convex polygon into smaller convex polygons may be found using the Tutte embedding.[3]
Hamiltonicity and shortness
Tait conjectured that every cubic polyhedral graph (that is, a polyhedral graph in which each vertex is incident to exactly three edges) has a Hamiltonian cycle, but this conjecture was disproved by a counterexample of W. T. Tutte, the polyhedral but non-Hamiltonian Tutte graph. If one relaxes the requirement that the graph be cubic, there are much smaller non-Hamiltonian polyhedral graphs. The graph with the fewest vertices and edges is the 11-vertex and 18-edge Herschel graph,[4] and there also exists an 11-vertex non-Hamiltonian polyhedral graph in which all faces are triangles, the Goldner–Harary graph.[5]
More strongly, there exists a constant [math]\displaystyle{ \alpha\lt 1 }[/math] (the shortness exponent) and an infinite family of polyhedral graphs such that the length of the longest simple path of an [math]\displaystyle{ n }[/math]-vertex graph in the family is [math]\displaystyle{ O(n^{\alpha}) }[/math].[6][7]
Combinatorial enumeration
Duijvestijn provides a count of the polyhedral graphs with up to 26 edges;[8] The number of these graphs with 6, 7, 8, ... edges is
- 1, 0, 1, 2, 2, 4, 12, 22, 58, 158, 448, 1342, 4199, 13384, 43708, 144810, ... (sequence A002840 in the OEIS).
One may also enumerate the polyhedral graphs by their numbers of vertices: for graphs with 4, 5, 6, ... vertices, the number of polyhedral graphs is
- 1, 2, 7, 34, 257, 2606, 32300, 440564, 6384634, 96262938, 1496225352, ... (sequence A000944 in the OEIS).
Special cases
A polyhedral graph is the graph of a simple polyhedron if it is cubic (every vertex has three edges), and it is the graph of a simplicial polyhedron if it is a maximal planar graph. The Halin graphs, graphs formed from a planar embedded tree by adding an outer cycle connecting all of the leaves of the tree, form another important subclass of the polyhedral graphs.
References
- ↑ Ziegler, Günter M. (1995), "Chapter 4: Steinitz' Theorem for 3-Polytopes", Lectures on Polytopes, pp. 103–126, ISBN 0-387-94365-X
- ↑ Grünbaum, Branko (2003), Convex Polytopes, Graduate Texts in Mathematics, 221 (2nd ed.), Springer-Verlag, ISBN 978-0-387-40409-7.
- ↑ "How to draw a graph", Proceedings of the London Mathematical Society 13: 743–767, 1963, doi:10.1112/plms/s3-13.1.743.
- ↑ Barnette, David; Jucovič, Ernest (1970), "Hamiltonian circuits on 3-polytopes", Journal of Combinatorial Theory 9 (1): 54–59, doi:10.1016/S0021-9800(70)80054-0
- ↑ Goldner, A.; Harary, F. (1975), "Note on a smallest nonhamiltonian maximal planar graph", Bull. Malaysian Math. Soc. 6 (1): 41–42
- ↑ Grünbaum, Branko; Motzkin, T. S. (1962), "Longest simple paths in polyhedral graphs", Journal of the London Mathematical Society s1-37 (1): 152–160, doi:10.1112/jlms/s1-37.1.152
- ↑ Owens, Peter J. (1999), "Shortness parameters for polyhedral graphs", Discrete Mathematics 206 (1–3): 159–169, doi:10.1016/S0012-365X(98)00402-6
- ↑ Duijvestijn, A. J. W. (1996), "The number of polyhedral (3-connected planar) graphs", Mathematics of Computation 65 (215): 1289–1293, doi:10.1090/S0025-5718-96-00749-1, https://ris.utwente.nl/ws/files/7051864/number_of_plyhedral.pdf.
External links
 |