Tutte embedding

Short description: Planar graph drawn by relaxing springs

In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average (or barycenter) of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

Example

Tutte embedding of the graph of a cube. The outer four vertices are fixed at the corners of a unit square and each remaining vertex is at the average of its neighbors' positions.

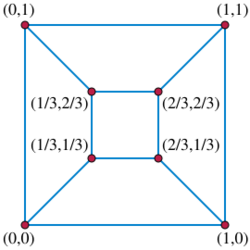
Let G be the graph of a cube, and (selecting one of its quadrilateral faces as the outer face) fix the four vertices of the outer face at the four corners of a unit square, the points whose x and y coordinates are all four combinations of zero and one. Then, if the remaining four vertices are placed at the four points whose x and y coordinates are combinations of 1/3 and 2/3, as in the figure, the result will be a Tutte embedding. For, at each interior vertex v of the embedding, and for each of the two coordinates, the three neighbors of v have coordinate values that are equal to v, smaller by 1/3, and larger by 1/3; the average of these values is the same as the coordinate value of v itself.

System of linear equations

The condition that a vertex v be at the average of its neighbors' positions may be expressed as two linear equations, one for the x coordinate of v and another for the y coordinate of v. For a graph with n vertices, h of which are fixed in position on the outer face, there are two equations for each interior vertex and also two unknowns (the coordinates) for each interior vertex. Therefore, this gives a system of linear equations with 2(n − h) equations in 2(n − h) unknowns, the solution to which is a Tutte embedding. As (Tutte 1963) showed, for 3-vertex-connected planar graphs, this system is non-degenerate. Therefore, it has a unique solution, and (with the outer face fixed) the graph has a unique Tutte embedding. This embedding can be found in polynomial time by solving the system of equations, for instance by using Gaussian elimination.

Polyhedral representation

By Steinitz's theorem, the 3-connected planar graphs to which Tutte's spring theorem applies coincide with the polyhedral graphs, the graphs formed by the vertices and edges of a convex polyhedron. According to the Maxwell–Cremona correspondence, a two-dimensional embedding of a planar graph forms the vertical projection of a three-dimensional convex polyhedron if and only if the embedding has an equilibrium stress, an assignment of forces to each edge (affecting both endpoints in equal and opposite directions parallel to the edge) such that the forces cancel at every vertex. For a Tutte embedding, assigning to each edge an attractive force proportional to its length (like a spring) makes the forces cancel at all interior vertices, but this is not necessarily an equilibrium stress at the vertices of the outer polygon. However, when the outer polygon is a triangle, it is possible to assign repulsive forces to its three edges to make the forces cancel there, too. In this way, Tutte embeddings can be used to find Schlegel diagrams of every convex polyhedron. For every 3-connected planar graph G, either G itself or the dual graph of G has a triangle, so either this gives a polyhedral representation of G or of its dual; in the case that the dual graph is the one with the triangle, polarization gives a polyhedral representation of G itself.

Applications in geometry processing

In geometry processing, Tutte's embedding is used for 2D uv-parametrization [math]\displaystyle{ \mathcal{S}^* }[/math]of 3D surfaces [math]\displaystyle{ \mathcal{S} }[/math] most commonly for the cases where the topology of the surface remains the same across [math]\displaystyle{ \mathcal{S} }[/math] and [math]\displaystyle{ \mathcal{S}^* }[/math](disk topology). Tutte's method minimizes the total distortion energy of the parametrized space by considering each transformed vertex as a point mass, and edges across the corresponding vertices as springs. The tightness of each spring is determined by the length of the edges in the original 3D surface to preserve the shape. Since it is reasonable to have smaller parametrized edge lengths for the smaller edges of [math]\displaystyle{ \mathcal{S} }[/math], and larger parametrized edge lengths for the larger edges of [math]\displaystyle{ \mathcal{S} }[/math], the spring constants [math]\displaystyle{ w_{ij} }[/math]are usually taken as the inverse of the absolute distance between the vertices [math]\displaystyle{ i,~j }[/math] in the 3D space.

[math]\displaystyle{ \text{Distortion Energy,}~E=\Sigma _{(i,j)\in E(\mathcal{S})} ~w_{ij}~\|\textbf{u}_\text{i} - \textbf{u}_\text{j}\| ^ 2 \text{, where } w_{ij} = \frac{1}{\|\textbf{v}_\text{i} - \textbf{v}_\text{j}\|}\text{, } \{\textbf{u}_\text{i}\}\in\mathcal{S}^*\text{, }\{\textbf{v}_\text{i}\}\in\mathcal{S} }[/math]

where [math]\displaystyle{ E(\mathcal{S}) }[/math] represents the set of edges in the original 3D surface. When the weights [math]\displaystyle{ w_{ij} }[/math] are positive (as is the case above), it is guaranteed that the mapping is bijective without any inversions. But when no further constraints are applied, the solution that minimizes the distortion energy trivially collapses to a single point in the parametrized space.

Therefore, one must provide boundary conditions where a set of known vertices of the 3D surface are mapped to known points in the 2D parametrized space. One common way of choosing such boundary conditions is to consider the vertices on the largest boundary loop of the original 3D surface which can be then constrained to be mapped to the outer ring of a unit disk in the 2D parametrized space. Note that if the 3D surface is a manifold, the boundary edges can be detected by verifying that they belong to only one face of the mesh.

Applications of parametrization in graphics and animation include texture mapping, among many others.

Generalizations

(Colin de Verdière 1991) generalized Tutte's spring theorem to graphs on higher-genus surfaces with non-positive curvature, where edges are represented by geodesics; this result was later independently rediscovered by (Hass Scott). Analogous results for graphs embedded on a torus were independently proved by (Delgado-Friedrichs 2005), by (Gortler Gotsman), and by (Lovász 2019).

(Chilakamarri Dean) investigate three-dimensional graph embeddings of the graphs of four-dimensional polytopes, formed by the same method as Tutte's embedding: choose one facet of the polytope as being the outer face of a three-dimensional embedding, and fix its vertices into place as the vertices of a three-dimensional polyhedron in space. Let each remaining vertex of the polytope be free to move in space, and replace each edge of the polytope by a spring. Then, find the minimum-energy configuration of the system of springs. As they show, the system of equations obtained in this way is again non-degenerate, but it is unclear under what conditions this method will find an embedding that realizes all facets of the polytope as convex polyhedra.

Related results

The result that every simple planar graph can be drawn with straight line edges is called Fáry's theorem. The Tutte spring theorem proves this for 3-connected planar graphs, but the result is true more generally for planar graphs regardless of connectivity. Using the Tutte spring system for a graph that is not 3-connected may result in degeneracies, in which subgraphs of the given graph collapse onto a point or a line segment; however, an arbitrary planar graph may be drawn using the Tutte embedding by adding extra edges to make it 3-connected, drawing the resulting 3-connected graph, and then removing the extra edges.

A graph is k-vertex-connected, but not necessarily planar, if and only if it has a convex embedding into (k −1)-dimensional space in which an arbitrary k-tuple of vertices are placed at the vertices of a simplex and, for each remaining vertex v, the convex hull of the neighbors of v is full-dimensional with v in its interior. If such an embedding exists, one can be found by fixing the locations of the chosen k vertices and solving a system of equations that places each vertex at the average of its neighbors, just as in Tutte's planar embedding.

In finite element mesh generation, Laplacian smoothing is a common method for postprocessing a generated mesh to improve the quality of its elements; it is particularly popular for quadrilateral meshes, for which other methods such as Lloyd's algorithm for triangular mesh smoothing are less applicable. In this method, each vertex is moved to or towards the average of its neighbors' positions, but this motion is only performed for a small number of iterations, to avoid large distortions of element sizes or (in the case of non-convex mesh domains) tangled non-planar meshes.

Force-directed graph drawing systems continue to be a popular method for visualizing graphs, but these systems typically use more complicated systems of forces that combine attractive forces on graph edges (as in Tutte's embedding) with repulsive forces between arbitrary pairs of vertices. These additional forces may cause the system to have many locally stable configurations rather than, as in Tutte's embedding, a single global solution.