Soboleva modified hyperbolic tangent

From HandWiki
Revision as of 16:32, 6 February 2024 by AIposter (talk | contribs) (simplify)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Mathematical activation function in data analysis

The Soboleva modified hyperbolic tangent, also known as (parametric) Soboleva modified hyperbolic tangent activation function ([P]SMHTAF),[nb 1] is a special S-shaped function based on the hyperbolic tangent, given by

Equation Left tail control Right tail control
[math]\displaystyle{ \operatorname{smht}x = \frac {e^{ax} - e^{-bx}} {e^{cx} + e^{-dx}}. }[/math]
SMHTAF 01.png
SMHTAF 02.png

History

This function was originally proposed as "modified hyperbolic tangent"[nb 1] by Ukrainian scientist Elena V. Soboleva (Елена В. Соболева) as a utility function for multi-objective optimization and choice modelling in decision-making.[1][2][3]

Practical usage

The function has since been introduced into neural network theory and practice.[4]

It was also used in economics for modelling consumption and investment,[5] to approximate current-voltage characteristics of field-effect transistors and light-emitting diodes,[6] to design antenna feeders,[7] and analyze plasma temperatures and densities in the divertor region of fusion reactors.[8]

Sensitivity to parameters

Derivative of the function is defined by the formula:

[math]\displaystyle{ \operatorname{smht}'(x) \doteq \frac {ae^{ax} + be^{-bx}} {e^{cx} + e^{-dx}} - \operatorname{smht}(x)\frac {ce^{cx} - de^{-dx}} {e^{cx} + e^{-dx}} }[/math]

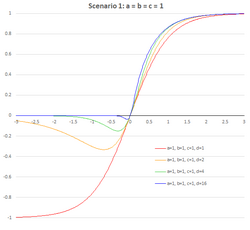
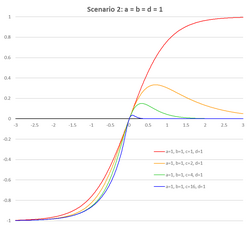
The following conditions are keeping the function limited on y-axes: a ≤ c, b ≤ d.

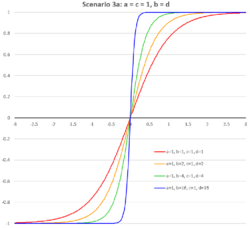
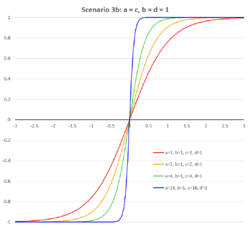
A family of recurrence-generated parametric Soboleva modified hyperbolic tangent activation functions (NPSMHTAF, FPSMHTAF) was studied with parameters a = c and b = d.[9] It is worth noting that in this case, the function is not sensitive to flipping the left and right-sides parameters:

Equation Left prevalence Right prevalence
[math]\displaystyle{ \frac {e^{ax} - e^{-bx}} {e^{ax} + e^{-bx}} = \frac {e^{bx} - e^{-ax}} {e^{bx} + e^{-ax}} }[/math]
SMHTAF 03a.png
SMHTAF 03b.png

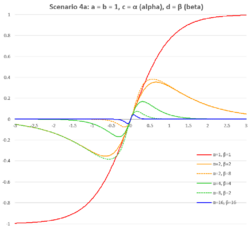
The function is sensitive to ratio of the denominator coefficients and often is used without coefficients in the numerator:

Equation Basic chart Scaled function
[math]\displaystyle{ \operatorname{ssht}x = \frac {e^{x} - e^{-x}} {e^{\alpha x} + e^{-\beta x}}. }[/math]

Extremum estimates: [math]\displaystyle{ x_{\min} = \frac {1} {2} \ln \frac {\beta-1} {\beta+1}; }[/math] [math]\displaystyle{ x_{\max} = \frac {1} {2} \ln \frac {\alpha+1} {\alpha-1}. }[/math]

SMHTAF 04a.png
SMHTAF 04b.png

With parameters a = b = c = d = 1 the modified hyperbolic tangent function reduces to the conventional tanh(x) function, whereas for a = b = 1 and c = d = 0, the term becomes equal to sinh(x).

See also

Notes

  1. ↑ 1.0 1.1 Soboleva proposed the name "modified hyperbolic tangent" (mtanh, mth), but since other authors used this name also for other functions, some authors have started to refer to this function as "Soboleva modified hyperbolic tangent".

References

  1. ↑ "The utility function in problems of structural optimization of distributed objects" (in ru). Четверта наукова конференція Харківського університету Повітряних Сил імені Івана Кожедуба, 16–17 квітня 2008 (The fourth scientific conference of the Ivan Kozhedub Kharkiv University of Air Forces, 16–17 April 2008). Kharkiv, Ukraine: Kharkiv University of Air Force (HUPS/ХУПС). 2008. p. 121. 
  2. ↑ (in ru). Материалы XIII Международного молодежного форума «Радиоэлектро-ника и молодежь в XXI веке» (Materials of the 13th international youth forum "Radioelectronics and youth in the 21st century"). Kharkiv, Ukraine: Kharkiv National University of Radioelectronics (KNURE/ХНУРЕ). 2009. p. 247. 
  3. ↑ (in ru)Problemy Bioniki: Respublikanskij Mežvedomstvennyj Naučno-Techničeskij Sbornik (Kharkiv National University of Radioelectronics (KNURE/ХНУРЕ)) 72 (1): 50–54. 2010. UDK 519.688: 004.896. ISSN 0555-2656. http://openarchive.nure.ua/bitstream/document/603/1/%D0%98%D0%94%D0%95%D0%9D%D0%A2%D0%98%D0%A4%D0%98%D0%9A%D0%90%D0%A6%D0%98%D0%AF%20%D0%A7%D0%90%D0%A1%D0%A2%D0%9D%D0%9E%D0%99%20%D0%9F%D0%9E%D0%9B%D0%95%D0%97%D0%9D%D0%9E%D0%A1%D0%A2%D0%98%20%D0%9C%D0%9D%D0%9E%D0%93%D0%9E%D0%A4%D0%90%D0%9A%D0%A2%D0%9E%D0%A0%D0%9D%D0%AB%D0%A5%20%D0%90%D0%9B%D0%AC%D0%A2%D0%95%D0%A0%D0%9D%D0%90%D0%A2%D0%98%D0%92%20%D0%A1%20%D0%9F%D0%9E%D0%9C%D0%9E%D0%A9%D0%AC%D0%AE%20S-%D0%9E%D0%91%D0%A0%D0%90%D0%97%D0%9D%D0%AB%D0%A5%20%D0%A4%D0%A3%D0%9D%D0%9A%D0%A6%D0%98%D0%99%20%2850-54%29.pdf. Retrieved 2020-06-19.  (5 pages) [1]
  4. ↑ "A Family Of Recurrence Generating Activation Functions Based On Gudermann Function". International Journal of Engineering Researches and Management Studies (Faculty of Mathematics and Informatics, University of Plovdiv "Paisii Hilendarski", Plovdiv, Bulgaria) 4 (8): 38–48. August 2017. ISSN 2394-7659. http://www.ijerms.com/DOC/Isues%20pdf/Archive-2017/August-2017/7.pdf. Retrieved 2020-06-19.  (11 pages) [2]
  5. ↑ Orlando, Giuseppe (2016-07-01). "A discrete mathematical model for chaotic dynamics in economics: Kaldor's model on business cycle". Mathematics and Computers in Simulation. 8th Workshop STRUCTURAL DYNAMICAL SYSTEMS: Computational Aspects; Edited by Nicoletta Del Buono, Roberto Garrappa and Giulia Spaletta and Nonstandard Applications of Computer Algebra (ACA’2013); Edited by Francisco Botana, Antonio Hernando, Eugenio Roanes-Lozano and Michael J. Wester 125: 83–98. doi:10.1016/j.matcom.2016.01.001. ISSN 0378-4754. https://www.sciencedirect.com/science/article/pii/S0378475416000045. 
  6. ↑ (in ru). Tomsk, Russia: Tomsk Politehnic University (TPU/ТПУ). 2009. pp. 135–138No. 4/314. http://cyberleninka.ru/article/n/primenenie-modifitsirovannoy-funktsii-giperbolicheskogo-tangensa-dlya-approksimatsii-voltampernyh-harakteristik-polevyh. Retrieved 2015-11-05.  (4 pages) [3]
  7. ↑ "Sigmoidal Functions In Antenna-Feeder Technique". International Journal of Pure and Applied Mathematics (Faculty of Mathematics and Informatics, University of Plovdiv "Paisii Hilendarski", Plovdiv, Bulgaria / Technical University of Sofia, Sofia, Bulgaria: Academic Publications, Ltd.) 116 (4): 1081–1092. 2017-11-23. doi:10.12732/ijpam.v116i4.23. ISSN 1311-8080. https://ijpam.eu/contents/2017-116-4/23/23.pdf. Retrieved 2020-06-19.  (12 pages)
  8. ↑ (in en, it, pt) Power Exhaust Data Analysis and Modeling Of Advanced Divertor Configuration (Thesis). Joint Research Doctorate In Fusion Science And Engineering Cycle XXX. Padova, Italy: Centro Ricerche Fusione (CRF), Università degli Studi di Padova / Università degli Studi di Napoli Federico II / Instituto Superior Técnico (IST), Universidade de Lisboa. 2018-01-15. p. 84. ID 10811. http://paduaresearch.cab.unipd.it/10811/1/Giulio_Rubino_Tesi.pdf. Retrieved 2020-06-19.  [4] (2+viii+3*iii+102 pages)
  9. ↑ "A Note on the Soboleva' Modified Hyperbolic Tangent Activation Function". International Journal of Innovative Science, Engineering & Technology (JISET) (Faculty of Mathematics and Informatics, University of Plovdiv "Paisii Hilendarski", Plovdiv, Bulgaria) 4 (6): 177–182. June 2017. ISSN 2348-7968. http://ijiset.com/vol4/v4s6/IJISET_V4_I06_21.pdf. Retrieved 2020-06-19.  (6 pages) [5]

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Soboleva_modified_hyperbolic_tangent&oldid=3366380"