Szeged index
In chemical graph theory, the Szeged index is a topological index of a molecule, used in biochemistry. The Szeged index, introduced by Iván Gutman,[1] generalizes the concept of the Wiener index introduced by Harry Wiener. The Szeged index of a connected graph G is defined as
- [math]\displaystyle{ Sz(G)=\sum_{e\in E(G)} n_1(e\mid G)n_2(e\mid G), }[/math]
If e is an edge of G connecting vertices u and v, then we write e = uv or e = vu. For [math]\displaystyle{ e=uv\in E(G) }[/math], let [math]\displaystyle{ n_1(e\mid G) }[/math] and [math]\displaystyle{ n_2(e\mid G) }[/math] be respectively the number of vertices of G lying closer to vertex u than to vertex v and the number of vertices of G lying closer to vertex v than to vertex u.
Szeged index plays an important role in information theory. One way to measure a network structure is through the so-called topological indices. Szeged index has been shown to correlate well with numerous biological and physicochemical properties.
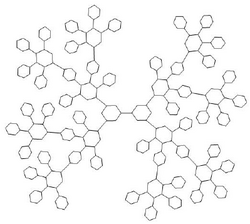
Examples
The Szeged index of Dendrimer Nanostar of the following figure can be calculated by[2]
- [math]\displaystyle{ Sz(T_n) = 1620n\cdot4^n - 2376\cdot4^n + 2862\cdot2^n-432, \quad n \geq 0. }[/math]
References
- ↑ Gutman, I. (1994), "A formula for the Wiener number of trees and its extension to graphs containing cycles", Graph Theory Notes, NY 27: 9–15.
- ↑ Khalifeh, M.H.; Darafsheh, M.R; Jolany, H. (2011), "The Wiener, Szeged, and PI Indices of a Dendrimer Nanostar", Journal of Computational and Theoretical Nanoscience 8 (2): 220–223, doi:10.1166/jctn.2011.1681, Bibcode: 2011JCTN....8..220K.
 |