ADALINE
ADALINE (Adaptive Linear Neuron or later Adaptive Linear Element) is an early single-layer artificial neural network and the name of the physical device that implemented this network.[1][2][3][4][5] The network uses memistors. It was developed by professor Bernard Widrow and his doctoral student Ted Hoff at Stanford University in 1960. It is based on the perceptron. It consists of a weight, a bias and a summation function.
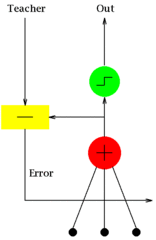
The difference between Adaline and the standard (McCulloch–Pitts) perceptron is in how they learn. Adaline unit weights are adjusted to match a teacher signal, before applying the Heaviside function (see figure), but the standard perceptron unit weights are adjusted to match the correct output, after applying the Heaviside function.
A multilayer network of ADALINE units is a MADALINE.
Definition
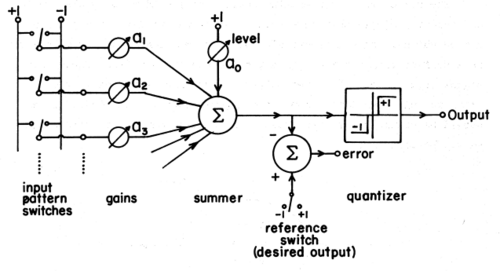
Adaline is a single layer neural network with multiple nodes where each node accepts multiple inputs and generates one output. Given the following variables as:
- [math]\displaystyle{ x }[/math] is the input vector
- [math]\displaystyle{ w }[/math] is the weight vector
- [math]\displaystyle{ n }[/math] is the number of inputs
- [math]\displaystyle{ \theta }[/math] some constant
- [math]\displaystyle{ y }[/math] is the output of the model
then we find that the output is [math]\displaystyle{ y=\sum_{j=1}^{n} x_j w_j + \theta }[/math]. If we further assume that
- [math]\displaystyle{ x_0 = 1 }[/math]
- [math]\displaystyle{ w_0 = \theta }[/math]
then the output further reduces to: [math]\displaystyle{ y=\sum_{j=0}^{n} x_j w_j }[/math]
Learning rule
The learning rule used by ADALINE is the LMS ("least mean squares") algorithm, a special case of gradient descent.
Define the following notations:
- [math]\displaystyle{ \eta }[/math] is the learning rate (some positive constant)
- [math]\displaystyle{ y }[/math] is the output of the model
- [math]\displaystyle{ o }[/math] is the target (desired) output
- [math]\displaystyle{ E=(o - y)^2 }[/math] is the square of the error.
The LMS algorithm updates the weights by [math]\displaystyle{ w \leftarrow w + \eta(o - y)x. }[/math]
This update rule minimizes [math]\displaystyle{ E }[/math], the square of the error,[6] and is in fact the stochastic gradient descent update for linear regression.[7]
MADALINE
MADALINE (Many ADALINE[8]) is a three-layer (input, hidden, output), fully connected, feed-forward artificial neural network architecture for classification that uses ADALINE units in its hidden and output layers, i.e. its activation function is the sign function.[9] The three-layer network uses memistors. Three different training algorithms for MADALINE networks, which cannot be learned using backpropagation because the sign function is not differentiable, have been suggested, called Rule I, Rule II and Rule III.
Despite many attempts, they never succeeded in training more than a single layer of weights in a MADALINE. This was until Widrow saw the backpropagation algorithm in a 1982 conference.[10]
MADALINE Rule 1 (MRI) - The first of these dates back to 1962.[11] It consists of two layers. The first layer is made of ADALINE units. Let the output of the i-th ADALINE unit be [math]\displaystyle{ o_i }[/math]. The second layer has two units. One is a majority-voting unit: it takes in all [math]\displaystyle{ o_i }[/math], and if there are more positives than negatives, then the unit outputs +1, and vice versa. Another is a "job assigner". Suppose the desired output is different from the majority-voted output, say the desired output is -1, then the job assigner calculates the minimal number of ADALINE units that must change their outputs from positive to negative, then picks those ADALINE units that are closest to being negative, and make them update their weights, according to the ADALINE learning rule. It was thought of as a form of "minimal disturbance principle".[12]
The largest MADALINE machine built had 1000 weights, each implemented by a memistor.[12]
MADALINE Rule 2 (MRII) - The second training algorithm improved on Rule I and was described in 1988.[8] The Rule II training algorithm is based on a principle called "minimal disturbance". It proceeds by looping over training examples, then for each example, it:
- finds the hidden layer unit (ADALINE classifier) with the lowest confidence in its prediction,
- tentatively flips the sign of the unit,
- accepts or rejects the change based on whether the network's error is reduced,
- stops when the error is zero.
MADALINE Rule 3 - The third "Rule" applied to a modified network with sigmoid activations instead of signum; it was later found to be equivalent to backpropagation.[12]
Additionally, when flipping single units' signs does not drive the error to zero for a particular example, the training algorithm starts flipping pairs of units' signs, then triples of units, etc.[8]
See also
References
- ↑ Anderson, James A.; Rosenfeld, Edward (2000). Talking Nets: An Oral History of Neural Networks. ISBN 9780262511117. https://books.google.com/books?id=-l-yim2lNRUC&q=adaline+smithsonian+widrow&pg=PA54.
- ↑ Youtube: widrowlms: Science in Action
- ↑ 1960: An adaptive "ADALINE" neuron using chemical "memistors"
- ↑ Youtube: widrowlms: The LMS algorithm and ADALINE. Part I - The LMS algorithm
- ↑ Youtube: widrowlms: The LMS algorithm and ADALINE. Part II - ADALINE and memistor ADALINE
- ↑ "Adaline (Adaptive Linear)". CS 4793: Introduction to Artificial Neural Networks. Department of Computer Science, University of Texas at San Antonio. http://www.cs.utsa.edu/~bylander/cs4793/learnsc32.pdf.
- ↑ Avi Pfeffer. "CS181 Lecture 5 — Perceptrons". Harvard University. http://www.seas.harvard.edu/courses/cs181/files/lecture05-notes.pdf.[yes|permanent dead link|dead link}}]
- ↑ 8.0 8.1 8.2 Rodney Winter; Bernard Widrow (1988). "MADALINE RULE II: A training algorithm for neural networks". IEEE International Conference on Neural Networks. pp. 401–408. doi:10.1109/ICNN.1988.23872. http://www-isl.stanford.edu/~widrow/papers/c1988madalinerule.pdf.
- ↑ Youtube: widrowlms: Science in Action (Madaline is mentioned at the start and at 8:46)
- ↑ Anderson, James A., ed (2000) (in en). Talking Nets: An Oral History of Neural Networks. The MIT Press. doi:10.7551/mitpress/6626.003.0004. ISBN 978-0-262-26715-1. https://direct.mit.edu/books/book/4886/Talking-NetsAn-Oral-History-of-Neural-Networks.
- ↑ Widrow, Bernard (1962). "Generalization and information storage in networks of adaline neurons". Self-organizing Systems: 435–461. https://isl.stanford.edu/~widrow/papers/c1961generalizationand.pdf.
- ↑ 12.0 12.1 12.2 Widrow, Bernard; Lehr, Michael A. (1990). "30 years of adaptive neural networks: perceptron, madaline, and backpropagation". Proceedings of the IEEE 78 (9): 1415–1442. doi:10.1109/5.58323.
External links
- "Delta Learning Rule: ADALINE". Artificial Neural Networks. Universidad Politécnica de Madrid. http://www.gc.ssr.upm.es/inves/neural/ann1/supmodel/linanet.htm.
- "Memristor-Based Multilayer Neural Networks With Online Gradient Descent Training". Implementation of the ADALINE algorithm with memristors in analog computing.
 |