Perceptron
In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function that can decide whether or not an input, represented by a vector of numbers, belongs to some specific class.[1] It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.
History


The artificial neuron network was invented in 1943 by Warren McCulloch and Walter Pitts in A logical calculus of the ideas immanent in nervous activity.[5]
In 1957, Frank Rosenblatt was at the Cornell Aeronautical Laboratory. He simulated the perceptron on an IBM 704.[6][7] Later, he obtained funding by the Information Systems Branch of the United States Office of Naval Research and the Rome Air Development Center, to build a custom-made computer, the Mark I Perceptron. It was first publicly demonstrated on 23 June 1960.[8] The machine was "part of a previously secret four-year NPIC [the US' National Photographic Interpretation Center] effort from 1963 through 1966 to develop this algorithm into a useful tool for photo-interpreters".[9]
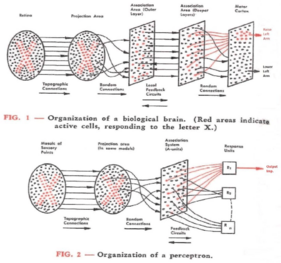
Rosenblatt described the details of the perceptron in a 1958 paper.[10] His organization of a perceptron is constructed of three kinds of cells ("units"): AI, AII, R, which stand for "projection", "association" and "response". He presented at the first international symposium on AI, Mechanisation of Thought Processes, which took place in 1958 November.[11]
Rosenblatt's project was funded under Contract Nonr-401(40) "Cognitive Systems Research Program", which lasted from 1959 to 1970,[12] and Contract Nonr-2381(00) "Project PARA" ("PARA" means "Perceiving and Recognition Automata"), which lasted from 1957[6] to 1963.[13]
In 1959, the Institute for Defense Analysis awarded his group a $10,000 contract. By September 1961, the ONR awarded further $153,000 worth of contracts, with $108,000 committed for 1962.[14]
The ONR research manager, Marvin Denicoff, stated that ONR, instead of ARPA, funded the Perceptron project, because the project was unlikely to produce technological results in the near or medium term. Funding from ARPA go up to the order of millions dollars, while from ONR are on the order of 10,000 dollars. Meanwhile, the head of IPTO at ARPA, J.C.R. Licklider, was interested in 'self-organizing', 'adaptive' and other biologically-inspired methods in the 1950s; but by the mid-1960s he was openly critical of these, including the perceptron. Instead he strongly favored the logical AI approach of Simon and Newell.[15]
Mark I Perceptron machine
The perceptron was intended to be a machine, rather than a program, and while its first implementation was in software for the IBM 704, it was subsequently implemented in custom-built hardware as the Mark I Perceptron with the project name "Project PARA",[16] designed for image recognition. The machine is currently in Smithsonian National Museum of American History.[17]
The Mark I Perceptron had three layers. One version was implemented as follows:
- An array of 400 photocells arranged in a 20x20 grid, named "sensory units" (S-units), or "input retina". Each S-unit can connect to up to 40 A-units.
- A hidden layer of 512 perceptrons, named "association units" (A-units).
- An output layer of eight perceptrons, named "response units" (R-units).
Rosenblatt called this three-layered perceptron network the alpha-perceptron, to distinguish it from other perceptron models he experimented with.[8]
The S-units are connected to the A-units randomly (according to a table of random numbers) via a plugboard (see photo), to "eliminate any particular intentional bias in the perceptron". The connection weights are fixed, not learned. Rosenblatt was adamant about the random connections, as he believed the retina was randomly connected to the visual cortex, and he wanted his perceptron machine to resemble human visual perception.[18]
The A-units are connected to the R-units, with adjustable weights encoded in potentiometers, and weight updates during learning were performed by electric motors.[2]: 193 The hardware details are in an operators' manual.[16]

In a 1958 press conference organized by the US Navy, Rosenblatt made statements about the perceptron that caused a heated controversy among the fledgling AI community; based on Rosenblatt's statements, The New York Times reported the perceptron to be "the embryo of an electronic computer that [the Navy] expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence."[19]
The Photo Division of Central Intelligence Agency, from 1960 to 1964, studied the use of Mark I Perceptron machine for recognizing militarily interesting silhouetted targets (such as planes and ships) in aerial photos.[20][21]
Principles of Neurodynamics (1962)
Rosenblatt described his experiments with many variants of the Perceptron machine in a book Principles of Neurodynamics (1962). The book is a published version of the 1961 report.[22]
Among the variants are:
- "cross-coupling" (connections between units within the same layer) with possibly closed loops,
- "back-coupling" (connections from units in a later layer to units in a previous layer),
- four-layer perceptrons where the last two layers have adjustable weights (and thus a proper multilayer perceptron),
- incorporating time-delays to perceptron units, to allow for processing sequential data,
- analyzing audio (instead of images).
The machine was shipped from Cornell to Smithsonian in 1967, under a government transfer administered by the Office of Naval Research.[9]
Perceptrons (1969)
Although the perceptron initially seemed promising, it was quickly proved that perceptrons could not be trained to recognise many classes of patterns. This caused the field of neural network research to stagnate for many years, before it was recognised that a feedforward neural network with two or more layers (also called a multilayer perceptron) had greater processing power than perceptrons with one layer (also called a single-layer perceptron).
Single-layer perceptrons are only capable of learning linearly separable patterns.[23] For a classification task with some step activation function, a single node will have a single line dividing the data points forming the patterns. More nodes can create more dividing lines, but those lines must somehow be combined to form more complex classifications. A second layer of perceptrons, or even linear nodes, are sufficient to solve many otherwise non-separable problems.
In 1969, a famous book entitled Perceptrons by Marvin Minsky and Seymour Papert showed that it was impossible for these classes of network to learn an XOR function. It is often incorrectly believed that they also conjectured that a similar result would hold for a multi-layer perceptron network. However, this is not true, as both Minsky and Papert already knew that multi-layer perceptrons were capable of producing an XOR function. (See the page on Perceptrons (book) for more information.) Nevertheless, the often-miscited Minsky and Papert text caused a significant decline in interest and funding of neural network research. It took ten more years until neural network research experienced a resurgence in the 1980s.[23] This text was reprinted in 1987 as "Perceptrons - Expanded Edition" where some errors in the original text are shown and corrected.
Subsequent work
Rosenblatt continued working on perceptrons despite diminishing funding. The last attempt was Tobermory, built between 1961 and 1967, built for speech recognition.[24] It occupied an entire room.[25] It had 4 layers with 12,000 weights implemented by toroidal magnetic cores. By the time of its completion, simulation on digital computers had become faster than purpose-built perceptron machines.[26] He died in a boating accident in 1971.
A simulation program for neural networks was written for IBM 7090/7094, and was used to study various pattern recognition applications, such as character recognition, particle tracks in bubble-chamber photographs; phoneme, isolated word, and continuous speech recognition; speaker verification; and center-of-attention mechanisms for image processing.[27][28]

The kernel perceptron algorithm was already introduced in 1964 by Aizerman et al.[29] Margin bounds guarantees were given for the Perceptron algorithm in the general non-separable case first by Freund and Schapire (1998),[1] and more recently by Mohri and Rostamizadeh (2013) who extend previous results and give new and more favorable L1 bounds.[30][31]
The perceptron is a simplified model of a biological neuron. While the complexity of biological neuron models is often required to fully understand neural behavior, research suggests a perceptron-like linear model can produce some behavior seen in real neurons.[32]
The solution spaces of decision boundaries for all binary functions and learning behaviors are studied in.[33]
Definition

In the modern sense, the perceptron is an algorithm for learning a binary classifier called a threshold function: a function that maps its input
(a real-valued vector) to an output value
(a single binary value):
where is the Heaviside step-function (where an input of outputs 1; otherwise 0 is the output ), is a vector of real-valued weights, is the dot product , where m is the number of inputs to the perceptron, and b is the bias. The bias shifts the decision boundary away from the origin and does not depend on any input value.
Equivalently, since , we can add the bias term as another weight and add a coordinate to each input , and then write it as a linear classifier that passes the origin:
The binary value of (0 or 1) is used to perform binary classification on as either a positive or a negative instance. Spatially, the bias shifts the position (though not the orientation) of the planar decision boundary.
In the context of neural networks, a perceptron is an artificial neuron using the Heaviside step function as the activation function. The perceptron algorithm is also termed the single-layer perceptron, to distinguish it from a multilayer perceptron, which is a misnomer for a more complicated neural network. As a linear classifier, the single-layer perceptron is the simplest feedforward neural network.
Power of representation
Information theory
From an information theory point of view, a single perceptron with K inputs has a capacity of 2K bits of information.[34] This result is due to Thomas Cover.[35]
Specifically let be the number of ways to linearly separate N points in K dimensions, thenWhen K is large, is very close to one when , but very close to zero when . In words, one perceptron unit can almost certainly memorize a random assignment of binary labels on N points when , but almost certainly not when .
Boolean function
When operating on only binary inputs, a perceptron is called a linearly separable Boolean function, or threshold Boolean function. The sequence of numbers of threshold Boolean functions on n inputs is OEIS A000609. The value is only known exactly up to case, but the order of magnitude is known quite exactly: it has upper bound and lower bound .[36]
Any Boolean linear threshold function can be implemented with only integer weights. Furthermore, the number of bits necessary and sufficient for representing a single integer weight parameter is .[36]
Universal approximation theorem
A single perceptron can learn to classify any half-space. It cannot solve any linearly nonseparable vectors, such as the Boolean exclusive-or problem (the famous "XOR problem").
A perceptron network with one hidden layer can learn to classify any compact subset arbitrarily closely. Similarly, it can also approximate any compactly-supported continuous function arbitrarily closely. This is essentially a special case of the theorems by George Cybenko and Kurt Hornik.
Conjunctively local perceptron
Perceptrons (Minsky and Papert, 1969) studied the kind of perceptron networks necessary to learn various Boolean functions.
Consider a perceptron network with input units, one hidden layer, and one output, similar to the Mark I Perceptron machine. It computes a Boolean function of type . They call a function conjunctively local of order , iff there exists a perceptron network such that each unit in the hidden layer connects to at most input units.
Theorem. (Theorem 3.1.1): The parity function is conjunctively local of order .
Theorem. (Section 5.5): The connectedness function is conjunctively local of order .
Learning algorithm for a single-layer perceptron

Below is an example of a learning algorithm for a single-layer perceptron with a single output unit. For a single-layer perceptron with multiple output units, since the weights of one output unit are completely separate from all the others', the same algorithm can be run for each output unit.
For multilayer perceptrons, where a hidden layer exists, more sophisticated algorithms such as backpropagation must be used. If the activation function or the underlying process being modeled by the perceptron is nonlinear, alternative learning algorithms such as the delta rule can be used as long as the activation function is differentiable. Nonetheless, the learning algorithm described in the steps below will often work, even for multilayer perceptrons with nonlinear activation functions.
When multiple perceptrons are combined in an artificial neural network, each output neuron operates independently of all the others; thus, learning each output can be considered in isolation.
Definitions
We first define some variables:
- is the learning rate of the perceptron. Learning rate is a positive number usually chosen to be less than 1. The larger the value, the greater the chance for volatility in the weight changes.
- is the training set of samples, where:
- is the th input vector from the -dimensional Euclidean space .
- is the desired output value of the perceptron for that input.
We show the values of the features as follows:
- is the value of the th feature of the th training input vector.
- .
To represent the weights:
- is the th value in the weight vector, to be multiplied by the value of the th input feature.
- Because , the is effectively a bias that we use instead of the bias constant .
To show the time-dependence of , we use:
- is the weight at time .
Steps
- Initialize the weights. Weights may be initialized to 0 or to a small random value. In the example below, we use 0. Set the time counter to 0.
- For each example j in our training set D, perform the following steps over the input and desired output :
- Calculate the output with the current weight vector :
- Update the weights:
- , for all features , is the learning rate.
- Increment the time counter:
- Calculate the output with the current weight vector :
For offline learning, the second step may be repeated until the iteration error is less than a user-specified error threshold , or a predetermined number of iterations have been completed, where s is again the size of the sample set.
The algorithm updates the weights after every training sample in step 2b, though one may note that the weights remain unchanged whenever .
Convergence of one perceptron on a linearly separable dataset
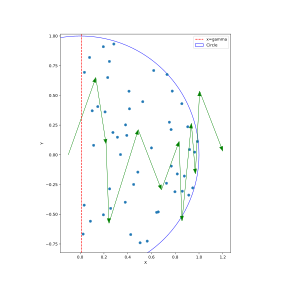
A single perceptron is a linear classifier. It can only reach a stable state if all input vectors are classified correctly. In case the training set D is not linearly separable, i.e. if the positive examples cannot be separated from the negative examples by a hyperplane, then the algorithm would not converge since there is no solution. Hence, if linear separability of the training set is not known a priori, one of the training variants below should be used. Detailed analysis and extensions to the convergence theorem are in Chapter 11 of Perceptrons (1969).
Linear separability is testable in time , where is the number of data points, and is the dimension of each point.[37]
If the training set is linearly separable, then the perceptron is guaranteed to converge after making finitely many mistakes.[38] The theorem is proved by Rosenblatt et al.
Perceptron convergence theorem — Given a dataset , such that , and it is linearly separable by some unit vector , with margin :
Then the perceptron 0-1 learning algorithm converges after making at most mistakes, for any learning rate, and any method of sampling from the dataset.
The following simple proof is due to Novikoff (1962). The idea of the proof is that the weight vector is always adjusted by a bounded amount in a direction with which it has a negative dot product, and thus can be bounded above by O(√t), where t is the number of changes to the weight vector. However, it can also be bounded below by O(t) because if there exists an (unknown) satisfactory weight vector, then every change makes progress in this (unknown) direction by a positive amount that depends only on the input vector.
Suppose at step , the perceptron with weight makes a mistake on data point , then it updates to .
If , the argument is symmetric, so we omit it.
WLOG, , then , , and .
By assumption, we have separation with margins: Thus,
Also and since the perceptron made a mistake, , and so
Since we started with , after making mistakes, but also
Combining the two, we have
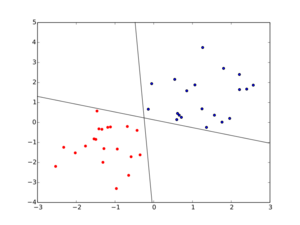
While the perceptron algorithm is guaranteed to converge on some solution in the case of a linearly separable training set, it may still pick any solution and problems may admit many solutions of varying quality.[39] The perceptron of optimal stability, nowadays better known as the linear support-vector machine, was designed to solve this problem (Krauth and Mezard, 1987).[40]
Perceptron cycling theorem
When the dataset is not linearly separable, then there is no way for a single perceptron to converge. However, we still have[41]
Perceptron cycling theorem — If the dataset has only finitely many points, then there exists an upper bound number , such that for any starting weight vector all weight vector has norm bounded by
This is proved first by Bradley Efron.[42]
Learning a Boolean function
Consider a dataset where the are from , that is, the vertices of an n-dimensional hypercube centered at origin, and . That is, all data points with positive have , and vice versa. By the perceptron convergence theorem, a perceptron would converge after making at most mistakes.
If we were to write a logical program to perform the same task, each positive example shows that one of the coordinates is the right one, and each negative example shows that its complement is a positive example. By collecting all the known positive examples, we eventually eliminate all but one coordinate, at which point the dataset is learned.[43]
This bound is asymptotically tight in terms of the worst-case. In the worst-case, the first presented example is entirely new, and gives bits of information, but each subsequent example would differ minimally from previous examples, and gives 1 bit each. After examples, there are bits of information, which is sufficient for the perceptron (with bits of information).[34]
However, it is not tight in terms of expectation if the examples are presented uniformly at random, since the first would give bits, the second bits, and so on, taking examples in total.[43]
Variants
The pocket algorithm with ratchet (Gallant, 1990) solves the stability problem of perceptron learning by keeping the best solution seen so far "in its pocket". The pocket algorithm then returns the solution in the pocket, rather than the last solution. It can be used also for non-separable data sets, where the aim is to find a perceptron with a small number of misclassifications. However, these solutions appear purely stochastically and hence the pocket algorithm neither approaches them gradually in the course of learning, nor are they guaranteed to show up within a given number of learning steps.
The Maxover algorithm (Wendemuth, 1995) is "robust" in the sense that it will converge regardless of (prior) knowledge of linear separability of the data set.[44] In the linearly separable case, it will solve the training problem – if desired, even with optimal stability (maximum margin between the classes). For non-separable data sets, it will return a solution with a computable small number of misclassifications.[45] In all cases, the algorithm gradually approaches the solution in the course of learning, without memorizing previous states and without stochastic jumps. Convergence is to global optimality for separable data sets and to local optimality for non-separable data sets.
The Voted Perceptron (Freund and Schapire, 1999), is a variant using multiple weighted perceptrons. The algorithm starts a new perceptron every time an example is wrongly classified, initializing the weights vector with the final weights of the last perceptron. Each perceptron will also be given another weight corresponding to how many examples do they correctly classify before wrongly classifying one, and at the end the output will be a weighted vote on all perceptrons.
In separable problems, perceptron training can also aim at finding the largest separating margin between the classes. The so-called perceptron of optimal stability can be determined by means of iterative training and optimization schemes, such as the Min-Over algorithm (Krauth and Mezard, 1987)[40] or the AdaTron (Anlauf and Biehl, 1989)).[46] AdaTron uses the fact that the corresponding quadratic optimization problem is convex. The perceptron of optimal stability, together with the kernel trick, are the conceptual foundations of the support-vector machine.
The -perceptron further used a pre-processing layer of fixed random weights, with thresholded output units. This enabled the perceptron to classify analogue patterns, by projecting them into a binary space. In fact, for a projection space of sufficiently high dimension, patterns can become linearly separable.
Another way to solve nonlinear problems without using multiple layers is to use higher order networks (sigma-pi unit). In this type of network, each element in the input vector is extended with each pairwise combination of multiplied inputs (second order). This can be extended to an n-order network.
It should be kept in mind, however, that the best classifier is not necessarily that which classifies all the training data perfectly. Indeed, if we had the prior constraint that the data come from equi-variant Gaussian distributions, the linear separation in the input space is optimal, and the nonlinear solution is overfitted.
Other linear classification algorithms include Winnow, support-vector machine, and logistic regression.
Multiclass perceptron
Like most other techniques for training linear classifiers, the perceptron generalizes naturally to multiclass classification. Here, the input and the output are drawn from arbitrary sets. A feature representation function maps each possible input/output pair to a finite-dimensional real-valued feature vector. As before, the feature vector is multiplied by a weight vector , but now the resulting score is used to choose among many possible outputs:
Learning again iterates over the examples, predicting an output for each, leaving the weights unchanged when the predicted output matches the target, and changing them when it does not. The update becomes:
This multiclass feedback formulation reduces to the original perceptron when is a real-valued vector, is chosen from , and .
For certain problems, input/output representations and features can be chosen so that can be found efficiently even though is chosen from a very large or even infinite set.
Since 2002, perceptron training has become popular in the field of natural language processing for such tasks as part-of-speech tagging and syntactic parsing (Collins, 2002). It has also been applied to large-scale machine learning problems in a distributed computing setting.[47]
References
- ↑ 1.0 1.1 Freund, Y.; Schapire, R. E. (1999). "Large margin classification using the perceptron algorithm". Machine Learning 37 (3): 277–296. doi:10.1023/A:1007662407062. http://cseweb.ucsd.edu/~yfreund/papers/LargeMarginsUsingPerceptron.pdf.
- ↑ 2.0 2.1 Bishop, Christopher M. (2006). Pattern Recognition and Machine Learning. Springer. ISBN 0-387-31073-8.
- ↑ Hecht-Nielsen, Robert (1991). Neurocomputing (Reprint. with corrections ed.). Reading (Mass.) Menlo Park (Calif.) New York [etc.]: Addison-Wesley. p. 6, Figure 1.3 caption.. ISBN 978-0-201-09355-1.
- ↑ Block, H. D. (1962-01-01). "The Perceptron: A Model for Brain Functioning. I" (in en). Reviews of Modern Physics 34 (1): 123–135. doi:10.1103/RevModPhys.34.123. ISSN 0034-6861. Bibcode: 1962RvMP...34..123B. https://link.aps.org/doi/10.1103/RevModPhys.34.123.
- ↑ McCulloch, W; Pitts, W (1943). "A Logical Calculus of Ideas Immanent in Nervous Activity". Bulletin of Mathematical Biophysics 5 (4): 115–133. doi:10.1007/BF02478259. https://www.bibsonomy.org/bibtex/13e8e0d06f376f3eb95af89d5a2f15957/schaul.
- ↑ 6.0 6.1 Rosenblatt, Frank (1957). "The Perceptron—a perceiving and recognizing automaton". Report 85-460-1 (Cornell Aeronautical Laboratory). https://bpb-us-e2.wpmucdn.com/websites.umass.edu/dist/a/27637/files/2016/03/rosenblatt-1957.pdf.
- ↑ Rosenblatt, Frank (March 1960). "Perceptron Simulation Experiments". Proceedings of the IRE 48 (3): 301–309. doi:10.1109/JRPROC.1960.287598. ISSN 0096-8390.
- ↑ 8.0 8.1 Nilsson, Nils J. (2009). "4.2.1. Perceptrons". The Quest for Artificial Intelligence. Cambridge: Cambridge University Press. ISBN 978-0-521-11639-8. https://www.cambridge.org/core/books/quest-for-artificial-intelligence/32C727961B24223BBB1B3511F44F343E.
- ↑ 9.0 9.1 O’Connor, Jack (2022-06-21). "Undercover Algorithm: A Secret Chapter in the Early History of Artificial Intelligence and Satellite Imagery" (in en). International Journal of Intelligence and CounterIntelligence: 1–15. doi:10.1080/08850607.2022.2073542. ISSN 0885-0607. https://www.tandfonline.com/doi/full/10.1080/08850607.2022.2073542.
- ↑ Rosenblatt, F. (1958). "The perceptron: A probabilistic model for information storage and organization in the brain.". Psychological Review 65 (6): 386–408. doi:10.1037/h0042519. ISSN 1939-1471. PMID 13602029. http://dx.doi.org/10.1037/h0042519.
- ↑ Frank Rosenblatt, ‘Two Theorems of Statistical Separability in the Perceptron’, Symposium on the Mechanization of Thought, National Physical Laboratory, Teddington, UK, November 1958, vol. 1, H. M. Stationery Office, London, 1959.
- ↑ Rosenblatt, Frank, and CORNELL UNIV ITHACA NY. Cognitive Systems Research Program. Technical report, Cornell University, 72, 1971.
- ↑ Muerle, John Ludwig, and CORNELL AERONAUTICAL LAB INC BUFFALO NY. Project Para, Perceiving and Recognition Automata. Cornell Aeronautical Laboratory, Incorporated, 1963.
- ↑ Penn, Jonathan (2021-01-11). Inventing Intelligence: On the History of Complex Information Processing and Artificial Intelligence in the United States in the Mid-Twentieth Century (Thesis). [object Object]. doi:10.17863/cam.63087.
- ↑ Guice, Jon (1998). "Controversy and the State: Lord ARPA and Intelligent Computing". Social Studies of Science 28 (1): 103–138. doi:10.1177/030631298028001004. ISSN 0306-3127. PMID 11619937. https://www.jstor.org/stable/285752.
- ↑ 16.0 16.1 16.2 Hay, John Cameron (1960). Mark I perceptron operators' manual (Project PARA) /. Buffalo: Cornell Aeronautical Laboratory. https://apps.dtic.mil/sti/tr/pdf/AD0236965.pdf.
- ↑ "Perceptron, Mark I" (in en). https://americanhistory.si.edu/collections/search/object/nmah_334414.
- ↑ Anderson, James A., ed (2000) (in en). Talking Nets: An Oral History of Neural Networks. The MIT Press. doi:10.7551/mitpress/6626.003.0004. ISBN 978-0-262-26715-1. https://direct.mit.edu/books/book/4886/Talking-NetsAn-Oral-History-of-Neural-Networks.
- ↑ Olazaran, Mikel (1996). "A Sociological Study of the Official History of the Perceptrons Controversy". Social Studies of Science 26 (3): 611–659. doi:10.1177/030631296026003005.
- ↑ "Perception Concepts to Photo-Interpretation". https://www.cia.gov/readingroom/document/cia-rdp78b04770a002300030027-6.
- ↑ Irwin, Julia A. (2024-09-11). "Artificial Worlds and Perceptronic Objects: The CIA's Mid-century Automatic Target Recognition" (in en). Grey Room (97): 6–35. doi:10.1162/grey_a_00415. ISSN 1526-3819. https://direct.mit.edu/grey/article/doi/10.1162/grey_a_00415/124337/Artificial-Worlds-and-Perceptronic-Objects-The-CIA.
- ↑ Principles of neurodynamics: Perceptrons and the theory of brain mechanisms, by Frank Rosenblatt, Report Number VG-1196-G-8, Cornell Aeronautical Laboratory, published on 15 March 1961. The work reported in this volume has been carried out under Contract Nonr-2381 (00) (Project PARA) at C.A.L. and Contract Nonr-401(40), at Cornell Univensity.
- ↑ 23.0 23.1 Sejnowski, Terrence J. (2018) (in en). The Deep Learning Revolution. MIT Press. p. 47. ISBN 978-0-262-03803-4. https://books.google.com/books?id=9xZxDwAAQBAJ.
- ↑ Rosenblatt, Frank (1962). “A Description of the Tobermory Perceptron.” Cognitive Research Program. Report No. 4. Collected Technical Papers, Vol. 2. Edited by Frank Rosenblatt. Ithaca, NY: Cornell University.
- ↑ 25.0 25.1 Nagy, George. 1963. System and circuit designs for the Tobermory perceptron. Technical report number 5, Cognitive Systems Research Program, Cornell University, Ithaca New York.
- ↑ Nagy, George. "Neural networks-then and now." IEEE Transactions on Neural Networks 2.2 (1991): 316-318.
- ↑ Barker, Trevor H. (1966-07-14). A Computer Program for Simulation of Perceptrons and Similar Neural Networks: Users' Manual (Technical Report). NONR 401 (40) and NSF GK-250. Ithaca, NY: Cornell University (published 1966). https://apps.dtic.mil/sti/html/trecms/AD0647611/.
- ↑ Nagy, George (March 1991). "Neural networks—then and now". IEEE Transactions on Neural Networks 2 (2): 316–318. doi:10.1109/72.80343. ISSN 1941-0093. PMID 18276386. https://sites.ecse.rpi.edu/~nagy/PDF_chrono/1991_Nagy_NN1991-ThenAndNow.pdf.
- ↑ Aizerman, M. A.; Braverman, E. M.; Rozonoer, L. I. (1964). "Theoretical foundations of the potential function method in pattern recognition learning". Automation and Remote Control 25: 821–837.
- ↑ Mohri, Mehryar; Rostamizadeh, Afshin (2013). "Perceptron Mistake Bounds". arXiv:1305.0208 [cs.LG].
- ↑ [1] Foundations of Machine Learning, MIT Press (Chapter 8).
- ↑ Cash, Sydney; Yuste, Rafael (1999). "Linear Summation of Excitatory Inputs by CA1 Pyramidal Neurons". Neuron 22 (2): 383–394. doi:10.1016/S0896-6273(00)81098-3. PMID 10069343.
- ↑ Liou, D.-R.; Liou, J.-W.; Liou, C.-Y. (2013). Learning Behaviors of Perceptron. iConcept Press. ISBN 978-1-477554-73-9.
- ↑ 34.0 34.1 MacKay, David (2003-09-25). Information Theory, Inference and Learning Algorithms. Cambridge University Press. p. 483. ISBN 9780521642989. https://books.google.com/books?id=AKuMj4PN_EMC&pg=PA483.
- ↑ Cover, Thomas M. (June 1965). "Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition". IEEE Transactions on Electronic Computers EC-14 (3): 326–334. doi:10.1109/PGEC.1965.264137. ISSN 0367-7508.
- ↑ 36.0 36.1 Šíma, Jiří; Orponen, Pekka (2003-12-01). "General-Purpose Computation with Neural Networks: A Survey of Complexity Theoretic Results" (in en). Neural Computation 15 (12): 2727–2778. doi:10.1162/089976603322518731. ISSN 0899-7667. PMID 14629867. https://direct.mit.edu/neco/article/15/12/2727-2778/6791.
- ↑ "Introduction to Machine Learning, Chapter 3: Perceptron" (in en). https://openlearninglibrary.mit.edu/courses/course-v1:MITx+6.036+1T2019/courseware/Week2/perceptron/?activate_block_id=block-v1:MITx+6.036+1T2019+type@sequential+block@perceptron.
- ↑ Novikoff, Albert J. (1963). "On convergence proofs for perceptrons". Office of Naval Research.
- ↑ Bishop, Christopher M (2006-08-17). "Chapter 4. Linear Models for Classification". Pattern Recognition and Machine Learning. Springer Science+Business Media, LLC. pp. 194. ISBN 978-0387-31073-2.
- ↑ 40.0 40.1 Krauth, W.; Mezard, M. (1987). "Learning algorithms with optimal stability in neural networks". Journal of Physics A: Mathematical and General 20 (11): L745–L752. doi:10.1088/0305-4470/20/11/013. Bibcode: 1987JPhA...20L.745K.
- ↑ Block, H. D.; Levin, S. A. (1970). "On the boundedness of an iterative procedure for solving a system of linear inequalities" (in en). Proceedings of the American Mathematical Society 26 (2): 229–235. doi:10.1090/S0002-9939-1970-0265383-5. ISSN 0002-9939. https://www.ams.org/proc/1970-026-02/S0002-9939-1970-0265383-5/.
- ↑ Efron, Bradley. "The perceptron correction procedure in nonseparable situations." Rome Air Dev. Center Tech. Doc. Rept (1964).
- ↑ 43.0 43.1 Simon, Herbert A.; Laird, John E. (2019-08-13). "Limits on Speed of Concept Attainment" (in English). The Sciences of the Artificial, reissue of the third edition with a new introduction by John Laird (Reissue ed.). Cambridge, Massachusetts London, England: The MIT Press. ISBN 978-0-262-53753-7.
- ↑ Wendemuth, A. (1995). "Learning the Unlearnable". Journal of Physics A: Mathematical and General 28 (18): 5423–5436. doi:10.1088/0305-4470/28/18/030. Bibcode: 1995JPhA...28.5423W.
- ↑ Wendemuth, A. (1995). "Performance of robust training algorithms for neural networks". Journal of Physics A: Mathematical and General 28 (19): 5485–5493. doi:10.1088/0305-4470/28/19/006. Bibcode: 1995JPhA...28.5485W.
- ↑ Anlauf, J. K.; Biehl, M. (1989). "The AdaTron: an Adaptive Perceptron algorithm". Europhysics Letters 10 (7): 687–692. doi:10.1209/0295-5075/10/7/014. Bibcode: 1989EL.....10..687A.
- ↑ McDonald, R.; Hall, K.; Mann, G. (2010). "Distributed Training Strategies for the Structured Perceptron". Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the ACL. Association for Computational Linguistics. pp. 456–464. https://www.aclweb.org/anthology/N10-1069.pdf.
Further reading
- Aizerman, M. A. and Braverman, E. M. and Lev I. Rozonoer. Theoretical foundations of the potential function method in pattern recognition learning. Automation and Remote Control, 25:821–837, 1964.
- Rosenblatt, Frank (1958), The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain, Cornell Aeronautical Laboratory, Psychological Review, v65, No. 6, pp. 386–408. doi:10.1037/h0042519.
- Rosenblatt, Frank (1962), Principles of Neurodynamics. Washington, DC: Spartan Books.
- Minsky, M. L. and Papert, S. A. 1969. Perceptrons. Cambridge, MA: MIT Press.
- Gallant, S. I. (1990). Perceptron-based learning algorithms. IEEE Transactions on Neural Networks, vol. 1, no. 2, pp. 179–191.
- Olazaran Rodriguez, Jose Miguel. A historical sociology of neural network research. PhD Dissertation. University of Edinburgh, 1991.
- Mohri, Mehryar and Rostamizadeh, Afshin (2013). Perceptron Mistake Bounds arXiv:1305.0208, 2013.
- Novikoff, A. B. (1962). On convergence proofs on perceptrons. Symposium on the Mathematical Theory of Automata, 12, 615–622. Polytechnic Institute of Brooklyn.
- Widrow, B., Lehr, M.A., "30 years of Adaptive Neural Networks: Perceptron, Madaline, and Backpropagation," Proc. IEEE, vol 78, no 9, pp. 1415–1442, (1990).
- Collins, M. 2002. Discriminative training methods for hidden Markov models: Theory and experiments with the perceptron algorithm in Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP '02).
- Yin, Hongfeng (1996), Perceptron-Based Algorithms and Analysis, Spectrum Library, Concordia University, Canada
External links
- A Perceptron implemented in MATLAB to learn binary NAND function
- Chapter 3 Weighted networks - the perceptron and chapter 4 Perceptron learning of Neural Networks - A Systematic Introduction by Raúl Rojas (ISBN 978-3-540-60505-8)
- History of perceptrons
- Mathematics of multilayer perceptrons
- Applying a perceptron model using scikit-learn - https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html
 |

