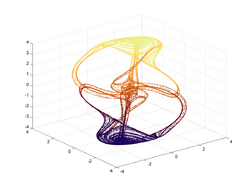
Thomas' cyclically symmetric attractor
In the dynamical systems theory, Thomas' cyclically symmetric attractor is a 3D strange attractor originally proposed by René Thomas.[1] It has a simple form which is cyclically symmetric in the x, y, and z variables and can be viewed as the trajectory of a frictionally dampened particle moving in a 3D lattice of forces.[2] The simple form has made it a popular example.
It is described by the differential equations
- [math]\displaystyle{ \frac{dx}{dt} = \sin(y)-bx }[/math]
- [math]\displaystyle{ \frac{dy}{dt} = \sin(z)-by }[/math]
- [math]\displaystyle{ \frac{dz}{dt} = \sin(x)-bz }[/math]
where [math]\displaystyle{ b }[/math] is a constant.
[math]\displaystyle{ b }[/math] corresponds to how dissipative the system is, and acts as a bifurcation parameter. For [math]\displaystyle{ b\gt 1 }[/math] the origin is the single stable equilibrium. At [math]\displaystyle{ b=1 }[/math] it undergoes a pitchfork bifurcation, splitting into two attractive fixed points. As the parameter is decreased further they undergo a Hopf bifurcation at [math]\displaystyle{ b\approx 0.32899 }[/math], creating a stable limit cycle. The limit cycle the undergoes a period doubling cascade and becomes chaotic at [math]\displaystyle{ b\approx 0.208186 }[/math]. Beyond this the attractor expands, undergoing a series of crises (up to six separate attractors can coexist for certain values). The fractal dimension of the attractor increases towards 3.[2]
In the limit [math]\displaystyle{ b=0 }[/math] the system lacks dissipation and the trajectory ergodically wanders the entire space (with an exception for 1.67%, where it drifts parallel to one of the coordinate axes: this corresponds to quasiperiodic torii). The dynamics has been described as deterministic fractional Brownian motion, and exhibits anomalous diffusion.[2][3]
References
- ↑ Thomas, René (1999). "Deterministic chaos seen in terms of feedback circuits: Analysis, synthesis, 'labyrinth chaos'". Int. J. Bifurc. Chaos 9 (10): 1889–1905. doi:10.1142/S0218127499001383. Bibcode: 1999IJBC....9.1889T.
- ↑ 2.0 2.1 2.2 Sprott, J. C.; Chlouverakis, Konstantinos E. (2007). "Labyrinth Chaos". Int. J. Bifurc. Chaos 17 (6): 2097. doi:10.1142/S0218127407018245. Bibcode: 2007IJBC...17.2097S.
- ↑ Rowlands, G.; Sprott, J. C. (2008). "A simple diffusion model showing anomalous scaling". Physics of Plasmas 15 (8): 082308. doi:10.1063/1.2969429. Bibcode: 2008PhPl...15h2308R.
 |