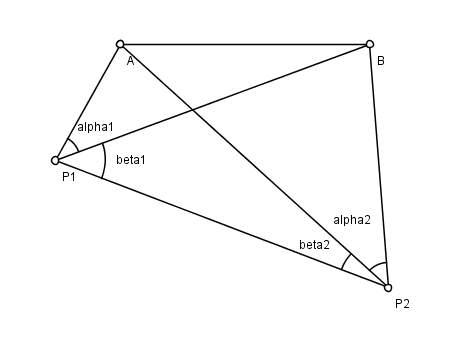
Hansen's problem

Short description: Fundamental topographical problem

In trigonometry, Hansen's problem is a problem in planar surveying, named after the astronomer Peter Andreas Hansen (1795–1874), who worked on the geodetic survey of Denmark. There are two known points A, B, and two unknown points P₁, P₂. From P₁ and P₂ an observer measures the angles made by the lines of sight to each of the other three points. The problem is to find the positions of P₁ and P₂. See figure; the angles measured are (α₁, β₁, α₂, β₂).

Since it involves observations of angles made at unknown points, the problem is an example of resection (as opposed to intersection).

Solution method overview

Define the following angles: [math]\displaystyle{ \begin{alignat}{5} \gamma &= \angle P_1 AP_2, &\quad \delta &= \angle P_1BP_2, \\[4pt] \phi &= \angle P_2 AB, &\quad \psi &= \angle P_1 BA. \end{alignat} }[/math] As a first step we will solve for φ and ψ. The sum of these two unknown angles is equal to the sum of β₁ and β₂, yielding the equation

[math]\displaystyle{ \phi + \psi = \beta_1 + \beta_2. }[/math]

A second equation can be found more laboriously, as follows. The law of sines yields

[math]\displaystyle{ \frac{\overline{AB}}{\overline{P_2 B}} = \frac{\sin \alpha_2}{\sin \phi}, \qquad \frac{\overline{P_2 B}}{\overline{P_1 P_2}} = \frac{\sin \beta_1}{\sin \delta}. }[/math]

Combining these, we get

[math]\displaystyle{ \frac{\overline{AB}}{\overline{P_1 P_2}} = \frac{\sin \alpha_2 \sin \beta_1}{\sin \phi \sin \delta}. }[/math]

Entirely analogous reasoning on the other side yields

[math]\displaystyle{ \frac{\overline{AB}}{\overline{P_1 P_2}} = \frac{\sin \alpha_1 \sin \beta_2}{\sin \psi \sin \gamma}. }[/math]

Setting these two equal gives

[math]\displaystyle{ \frac{\sin \phi}{\sin \psi} = \frac{\sin \gamma \sin \alpha_2 \sin \beta_1}{\sin \delta \sin \alpha_1 \sin \beta_2} = k. }[/math]

Using a known trigonometric identity this ratio of sines can be expressed as the tangent of an angle difference:

[math]\displaystyle{ \tan \tfrac12(\phi - \psi) = \frac{k-1}{k+1} \tan\tfrac12(\phi + \psi). }[/math]

Where [math]\displaystyle{ k = \frac{\sin \phi}{\sin \psi}. }[/math]

This is the second equation we need. Once we solve the two equations for the two unknowns φ, ψ, we can use either of the two expressions above for [math]\displaystyle{ \tfrac{\overline{AB}}{\overline{P_1 P_2}} }[/math] to find [math]\displaystyle{ \overline{P_1P_2} }[/math] since AB is known. We can then find all the other segments using the law of sines.

Solution algorithm

We are given four angles (α₁, β₁, α₂, β₂) and the distance AB. The calculation proceeds as follows:

• Calculate [math]\displaystyle{ \begin{align} \gamma &= \pi-\alpha_1-\beta_1-\beta_2, \\ \delta &= \pi-\alpha_2-\beta_1-\beta_2. \end{align} }[/math]
• Calculate [math]\displaystyle{ k = \frac{\sin \gamma \sin \alpha_2 \sin \beta_1}{\sin \delta \sin \alpha_1 \sin \beta_2}. }[/math]
• Let [math]\displaystyle{ s = \beta_1+\beta_2, \quad d = 2 \arctan \left( \frac{k-1}{k+1} \tan\tfrac12 s \right) }[/math] and then [math]\displaystyle{ \phi = \frac{s+d}{2}, \quad \psi = \frac{s-d}{2}. }[/math]
• Calculate [math]\displaystyle{ \overline{P_1 P_2} = \overline{AB} \ \frac{\sin \phi \sin \delta}{\sin \alpha_2 \sin \beta_1} }[/math] or equivalently [math]\displaystyle{ \overline{P_1 P_2} = \overline{AB} \ \frac{\sin \psi \sin \gamma}{\sin \alpha_1 \sin \beta_2}. }[/math] If one of these fractions has a denominator close to zero, use the other one.

See also

• Solving triangles
• Snell's problem