Snellius–Pothenot problem

Short description: Problem in trigonometry

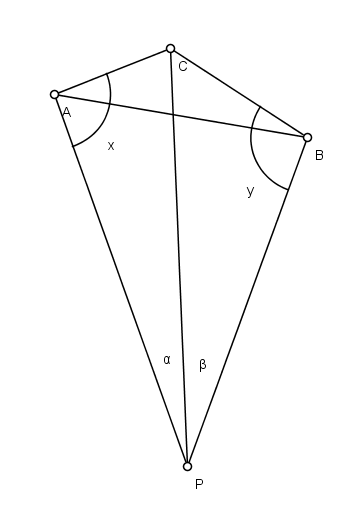
In trigonometry, the Snellius–Pothenot problem is a problem first described in the context of planar surveying. Given three known points A, B, C, an observer at an unknown point P observes that the line segment AC subtends an angle α and the segment CB subtends an angle β; the problem is to determine the position of the point P. (See figure; the point denoted C is between A and B as seen from P).

Since it involves the observation of known points from an unknown point, the problem is an example of resection. Historically it was first studied by Snellius, who found a solution around 1615.

Formulating the equations

First equation

Denoting the (unknown) angles ∠CAP as x and ∠CBP as y gives:

[math]\displaystyle{ x+y = 2 \pi - \alpha - \beta - C }[/math]

by using the sum of the angles formula for the quadrilateral PACB. The variable C represents the (known) internal angle in this quadrilateral at point C. (Note that in the case where the points C and P are on the same side of the line AB, the angle ∠C will be greater than π).

Second equation

Applying the law of sines in triangles △PAC and △PBC, we can express PC in two different ways:

[math]\displaystyle{ \overline{PC} = \frac{\overline{AC} \sin x }{\sin \alpha} = \frac{\overline{BC} \sin y}{\sin \beta}. }[/math]

A useful trick at this point is to define an auxiliary angle φ such that

[math]\displaystyle{ \tan \phi = \frac{{\rm BC} \sin \alpha}{{\rm AC} \sin \beta}. }[/math]

(A minor note: one should be concerned about division by zero, but consider that the problem is symmetric, so if one of the two given angles is zero one can, if needed, rename that angle α and call the other (non-zero) angle β, reversing the roles of A and B as well. This will suffice to guarantee that the ratio above is well defined. An alternative approach to the zero angle problem is given in the algorithm below.)

With this substitution the equation becomes

[math]\displaystyle{ \frac{\sin x}{\sin y}=\tan \phi. }[/math]

Now two known trigonometric identities can be used, namely

[math]\displaystyle{ \tan \left(\tfrac{\pi}{4} - \phi\right) = \frac{1 - \tan\phi}{\tan\phi+1}\ , \qquad \frac{\tan\tfrac12(x-y)}{\tan\tfrac12(x+y)} = \frac{\sin x - \sin y}{\sin x + \sin y}\ , }[/math]

to put this in the form of the second equation;

[math]\displaystyle{ \tan\tfrac12(x-y) = \tan\tfrac12(\alpha + \beta + C) \tan \left(\tfrac{\pi}{4}-\phi\right). }[/math]

Now these two equations in two unknowns must be solved. Once x and y are known the various triangles can be solved straightforwardly to determine the position of P. The detailed procedure is shown below.

Solution algorithm

Given are two lengths AC, BC, and three angles α, β, C, the solution proceeds as follows.

• calculate [math]\displaystyle{ \phi= \mathsf{atan2}\left( \overline{BC} \sin \alpha,\ \overline{AC} \sin\beta \right), }[/math] where atan2 is a computer function, also called the arctangent of two arguments, that returns the arctangent of the ratio of the two values given. Note that in Microsoft Excel the two arguments are reversed, so the proper syntax would be = atan2(AC*\sin(beta), BC*\sin(alpha)). The atan2 function correctly handles the case where one of the two arguments is zero.
• calculate [math]\displaystyle{ K = 2 \pi -\alpha-\beta-C. }[/math]
• calculate [math]\displaystyle{ W = 2 \cdot \arctan\left[ \tan(\tfrac{\pi}{4} - \phi) \, \tan\tfrac12(\alpha+\beta+C)\right]. }[/math]
• find [math]\displaystyle{ x = \frac{K+W}{2}, \ y = \frac{K-W}{2}. }[/math]
• find [math]\displaystyle{ \overline{PC} = \begin{cases} \dfrac{\overline{BC} \sin y}{\sin \beta} & \text{if } |\sin \beta| \gt |\sin \alpha|, \\[4pt] \dfrac{\overline{AC} \sin x}{\sin \alpha} & \text{otherwise.} \end{cases} }[/math]
• find [math]\displaystyle{ \overline{PA} = \sqrt{\overline{AC}^2 + \overline{PC}^2 - 2 \cdot \overline{AC} \cdot \overline{PC} \cdot \cos(\pi-\alpha-x)}. }[/math] (This comes from the law of cosines.)
• find [math]\displaystyle{ \overline{PB} = \sqrt{\overline{BC}^2 + \overline{PC}^2 - 2\cdot \overline{BC} \cdot \overline{PC} \cdot \cos(\pi-\beta-y)}. }[/math]

If the coordinates of [math]\displaystyle{ A: x_A,y_A }[/math] and [math]\displaystyle{ C: x_C,y_C }[/math] are known in some appropriate Cartesian coordinate system then the coordinates of P can be found as well.

Geometric (graphical) solution

By the inscribed angle theorem the locus of points from which AC subtends an angle α is a circle having its center on the midline of AC; from the center O of this circle, AC subtends an angle 2α. Similarly the locus of points from which CB subtends an angle β is another circle. The desired point P is at the intersection of these two loci.

Therefore, on a map or nautical chart showing the points A, B, C, the following graphical construction can be used:

• Draw the segment AC, the midpoint M and the midline, which crosses AC perpendicularly at M. On this line find the point O such that [math]\displaystyle{ \overline{MO} = \tfrac{\overline{AC}}{2 \tan \alpha}. }[/math] Draw the circle with center at O passing through A and C.
• Repeat the same construction with points B, C and the angle β.
• Mark P at the intersection of the two circles (the two circles intersect at two points; one intersection point is C and the other is the desired point P.)

This method of solution is sometimes called Cassini's method.

Rational trigonometry approach

The following solution is based upon a paper by N. J. Wildberger. It has the advantage that it is almost purely algebraic. The only place trigonometry is used is in converting the angles to spreads. There is only one square root required.

• define the following:[math]\displaystyle{ \begin{align} & s(x) = \sin^2x \\[4pt] & A(x,y,z) = (x+y+z)^2 - 2(x^2 + y^2 + z^2) \\[2pt] &\begin{alignat}{5} r_1 &= s(\beta) &\qquad Q_1 &= \overline{BC}^2 \\ r_2 &= s(\alpha) & Q_2 &= \overline{AC}^2 \\ r_3 &= s(\alpha + \beta) & Q_3 &= \overline{AB}^2 \end{alignat}\end{align} }[/math]
• now let:[math]\displaystyle{ \begin{align} R_1 &= \frac{r_2 Q_3}{r_3} \qquad R_2 = \frac{r_1 Q_3}{r_3} \\[4pt] C_0 &= \frac{(Q_1 + Q_2 + Q_3) (r_1 + r_2 + r_3) - 2 (Q_1 r_1 + Q_2 r_2 + Q_3 r_3)}{2 r_3} \\[4pt] D_0 &= \frac{r_1 r_2 A(Q_1,Q_2,Q_3)}{r_3} \end{align} }[/math]
• the following equation gives two possible values for R₃:[math]\displaystyle{ (R_3 - C_0)^2 = D_0 }[/math]
• choosing the larger of these values, let:[math]\displaystyle{ \begin{align} v_1 &= 1 - \frac{(R_1 + R_3 - Q_2)^2}{4 R_1 R_3} \\[4pt] v_2 &= 1 - \frac{(R_2 + R_3 - Q_1)^2}{4 R_2 R_3} \end{align} }[/math]
• finally:[math]\displaystyle{ \begin{align} \overline{AP}^2 &= \frac{v_1 R_1}{r_2} = \frac{v_1 Q_3}{r_3} \\[4pt] \overline{BP}^2 &= \frac{v_2 R_2}{r_1} = \frac{v_2 Q_3}{r_3} \end{align} }[/math]

The indeterminate case

When the point P happens to be located on the same circle as A, B, C, the problem has an infinite number of solutions; the reason is that from any other point P' located on the arc Template:Overarc of this circle the observer sees the same angles α and β as from P (inscribed angle theorem). Thus the solution in this case is not uniquely determined.

The circle through ABC is known as the "danger circle", and observations made on (or very close to) this circle should be avoided. It is helpful to plot this circle on a map before making the observations.

A theorem on cyclic quadrilaterals is helpful in detecting the indeterminate situation. The quadrilateral APBC is cyclic iff a pair of opposite angles (such as the angle at P and the angle at C) are supplementary i.e. iff [math]\displaystyle{ \alpha+\beta+C = k \pi, (k=1,2,\cdots) }[/math]. If this condition is observed the computer/spreadsheet calculations should be stopped and an error message ("indeterminate case") returned.

Solved examples

(Adapted form Bowser, exercise 140, page 203). A, B, C are three objects such that AC = 435 (yards), CB = 320, and ∠C = 255.8 degrees. From a station P it is observed that ∠APC = 30 degrees and ∠CPB = 15 degrees. Find the distances of P from A, B, C. (Note that in this case the points C and P are on the same side of the line AB, a different configuration from the one shown in the figure).

Answer: PA = 790, PB = 777, PC = 502.

A slightly more challenging test case for a computer program uses the same data but this time with ∠CPB = 0. The program should return the answers 843, 1157 and 837.

Naming controversy

Plaque on Snellius' house in Leiden

The British authority on geodesy, George Tyrrell McCaw (1870–1942) wrote that the proper term in English was Snellius problem, while Snellius-Pothenot was the continental European usage.

McCaw thought the name of Laurent Pothenot (1650–1732) did not deserve to be included as he had made no original contribution, but merely restated Snellius 75 years later.

See also

• Solution of triangles
• Triangulation (surveying)

Notes

• Gerhard Heindl: Analysing Willerding’s formula for solving the planar three point resection problem, Journal of Applied Geodesy, Band 13, Heft 1, Seiten 27–31, ISSN (Online) 1862-9024, ISSN (Print) 1862-9016, DOI: [1]

References

• Edward A. Bowser: A treatise on plane and spherical trigonometry, Washington D.C., Heath & Co., 1892, page 188 Google books