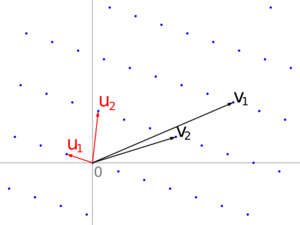
Lattice reduction
In mathematics, the goal of lattice basis reduction is to find a basis with short, nearly orthogonal vectors when given an integer lattice basis as input. This is realized using different algorithms, whose running time is usually at least exponential in the dimension of the lattice.
Nearly orthogonal
One measure of nearly orthogonal is the orthogonality defect. This compares the product of the lengths of the basis vectors with the volume of the parallelepiped they define. For perfectly orthogonal basis vectors, these quantities would be the same.
Any particular basis of [math]\displaystyle{ n }[/math] vectors may be represented by a matrix [math]\displaystyle{ B }[/math], whose columns are the basis vectors [math]\displaystyle{ b_i, i = 1, \ldots, n }[/math]. In the fully dimensional case where the number of basis vectors is equal to the dimension of the space they occupy, this matrix is square, and the volume of the fundamental parallelepiped is simply the absolute value of the determinant of this matrix [math]\displaystyle{ \det(B) }[/math]. If the number of vectors is less than the dimension of the underlying space, then volume is [math]\displaystyle{ \sqrt{\det(B^T B)} }[/math]. For a given lattice [math]\displaystyle{ \Lambda }[/math], this volume is the same (up to sign) for any basis, and hence is referred to as the determinant of the lattice [math]\displaystyle{ \det(\Lambda) }[/math] or lattice constant [math]\displaystyle{ d(\Lambda) }[/math].
The orthogonality defect is the product of the basis vector lengths divided by the parallelepiped volume;
- [math]\displaystyle{ \delta(B) = \frac{\Pi_{i=1}^n \|b_i\|}{\sqrt{\det(B^T B)}} = \frac{\Pi_{i=1}^n \|b_i\|}{d(\Lambda)} }[/math]
From the geometric definition it may be appreciated that [math]\displaystyle{ \delta(B) \ge 1 }[/math] with equality if and only if the basis is orthogonal.
If the lattice reduction problem is defined as finding the basis with the smallest possible defect, then the problem is NP-hard[citation needed]. However, there exist polynomial time algorithms to find a basis with defect [math]\displaystyle{ \delta(B) \le c }[/math] where c is some constant depending only on the number of basis vectors and the dimension of the underlying space (if different)[citation needed]. This is a good enough solution in many practical applications[citation needed].
In two dimensions
For a basis consisting of just two vectors, there is a simple and efficient method of reduction closely analogous to the Euclidean algorithm for the greatest common divisor of two integers. As with the Euclidean algorithm, the method is iterative; at each step the larger of the two vectors is reduced by adding or subtracting an integer multiple of the smaller vector.
The pseudocode of the algorithm, often known as Lagrange's algorithm or the Lagrange-Gauss algorithm, is as follows:
Input: [math]\displaystyle{ (u,v) }[/math] a basis for the lattice [math]\displaystyle{ L }[/math]. Assume that [math]\displaystyle{ ||v|| \leq ||u|| }[/math], otherwise swap them. Output: A basis [math]\displaystyle{ (u,v) }[/math] with [math]\displaystyle{ ||u|| = \lambda_1(L), ||v|| = \lambda_2(L) }[/math].
While [math]\displaystyle{ ||v|| \lt ||u|| }[/math]: [math]\displaystyle{ q := \lfloor {\langle u, \frac{ v}{||v||^2} \rangle } \rceil }[/math] # Round to nearest integer [math]\displaystyle{ r := u - qv }[/math] [math]\displaystyle{ u := v }[/math] [math]\displaystyle{ v := r }[/math]
See the section on Lagrange's algorithm in [1] for further details.
Applications
Lattice reduction algorithms are used in a number of modern number theoretical applications, including in the discovery of a spigot algorithm for [math]\displaystyle{ \pi }[/math]. Although determining the shortest basis is possibly an NP-complete problem, algorithms such as the LLL algorithm[2] can find a short (not necessarily shortest) basis in polynomial time with guaranteed worst-case performance. LLL is widely used in the cryptanalysis of public key cryptosystems.
When used to find integer relations, a typical input to the algorithm consists of an augmented [math]\displaystyle{ n \times n }[/math] identity matrix with the entries in the last column consisting of the [math]\displaystyle{ n }[/math] elements (multiplied by a large positive constant [math]\displaystyle{ w }[/math] to penalize vectors that do not sum to zero) between which the relation is sought.
The LLL algorithm for computing a nearly-orthogonal basis was used to show that integer programming in any fixed dimension can be done in polynomial time.[3]
Algorithms
The following algorithms reduce lattice bases; several public implementations of these algorithms are also listed.
| Year | Algorithm | Implementation |
|---|---|---|
| 1773 | Lagrange/Gauss reduction for 2D lattices | |
| 1982 | Lenstra–Lenstra–Lovász reduction | NTL, fplll |
| 1987 | Block Korkine–Zolotarev[4] | NTL, fplll |
| 1993 | Seysen Reduction[5] |
References
- ↑ Nguyen, Phong Q. (2009). "Hermite’s Constant and Lattice Algorithms". The LLL Algorithm. Information Security and Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 19–69. doi:10.1007/978-3-642-02295-1_2. ISBN 978-3-642-02294-4.
- ↑ Lenstra, A. K.; Lenstra, H. W. Jr.; Lovász, L. (1982). "Factoring polynomials with rational coefficients". Mathematische Annalen 261 (4): 515–534. doi:10.1007/BF01457454.
- ↑ "Integer programming with a fixed number of variables". Mathematics of Operations Research 8 (4): 538–548. 1983. doi:10.1287/moor.8.4.538.
- ↑ Hanrot, Guillaume; Stehlé, Damien (2008). "Worst-Case Hermite-Korkine-Zolotarev Reduced Lattice Bases". arXiv:0801.3331 [math.NT].
- ↑ Seysen, Martin (September 1993). "Simultaneous reduction of a lattice basis and its reciprocal basis". Combinatorica 13 (3): 363–376. doi:10.1007/BF01202355.
 |