Parallelepiped

Short description: Hexahedron with parallelogram faces

Parallelepiped
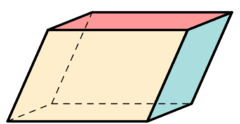
Type	Prism Plesiohedron
Faces	6 parallelograms
Edges	12
Vertices	8
Symmetry group	Ci, [2+,2+], (×), order 2
Properties	convex, zonohedron

In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term rhomboid is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square.

Three equivalent definitions of parallelepiped are

• a hexahedron with three pairs of parallel faces,
• a polyhedron with six faces (hexahedron), each of which is a parallelogram, and
• a prism of which the base is a parallelogram.

The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all specific cases of parallelepiped.

"Parallelepiped" is now usually pronounced /ˌpærəˌlɛlɪˈpɪpɪd/ or /ˌpærəˌlɛlɪˈpaɪpɪd/; traditionally it was /ˌpærəlɛlˈɛpɪpɛd/ PARR-ə-lel-EP-ih-ped despite its etymology in Greek παραλληλεπίπεδον parallelepipedon, a body "having parallel planes".

Parallelepipeds are a subclass of the prismatoids.

Properties

Any of the three pairs of parallel faces can be viewed as the base planes of the prism. A parallelepiped has three sets of four parallel edges; the edges within each set are of equal length.

Parallelepipeds result from linear transformations of a cube (for the non-degenerate cases: the bijective linear transformations).

Since each face has point symmetry, a parallelepiped is a zonohedron. Also the whole parallelepiped has point symmetry C_i (see also triclinic). Each face is, seen from the outside, the mirror image of the opposite face. The faces are in general chiral, but the parallelepiped is not.

A space-filling tessellation is possible with congruent copies of any parallelepiped.

Volume

Parallelepiped, generated by three vectors

A parallelepiped can be considered as an oblique prism with a parallelogram as base. Hence the volume [math]\displaystyle{ V }[/math] of a parallelepiped is the product of the base area [math]\displaystyle{ B }[/math] and the height [math]\displaystyle{ h }[/math] (see diagram). With

• [math]\displaystyle{ B = \left|\mathbf a\right| \cdot \left|\mathbf b\right| \cdot \sin \gamma = \left|\mathbf a \times \mathbf b\right| }[/math] (where [math]\displaystyle{ \gamma }[/math] is the angle between vectors [math]\displaystyle{ \mathbf a }[/math] and [math]\displaystyle{ \mathbf b }[/math]), and
• [math]\displaystyle{ h = \left|\mathbf c\right| \cdot \left|\cos \theta\right| }[/math] (where [math]\displaystyle{ \theta }[/math] is the angle between vector [math]\displaystyle{ \mathbf c }[/math] and the normal to the base), one gets:

[math]\displaystyle{ V = B\cdot h = \left(\left|\mathbf a\right| \left|\mathbf b\right| \sin \gamma\right) \cdot \left|\mathbf c\right| \left|\cos \theta\right| = \left|\mathbf a \times \mathbf b\right| \left|\mathbf c\right| \left|\cos \theta\right| = \left|\left(\mathbf{a} \times \mathbf{b}\right) \cdot \mathbf{c}\right|. }[/math] The mixed product of three vectors is called triple product. It can be described by a determinant. Hence for [math]\displaystyle{ \mathbf a=(a_1,a_2,a_3)^\mathsf{T}, ~\mathbf b=(b_1,b_2,b_3)^\mathsf{T}, ~\mathbf c=(c_1,c_2,c_3)^\mathsf{T}, }[/math] the volume is:

[math]\displaystyle{ V = \left| \det \begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix} \right| . }[/math]

(V1)

Another way to prove (V1) is to use the scalar component in the direction of [math]\displaystyle{ \mathbf a\times\mathbf b }[/math] of vector [math]\displaystyle{ \mathbf c }[/math]: [math]\displaystyle{ \begin{align} V = \left|\mathbf a\times\mathbf b\right| \left|\operatorname{scal}_{\mathbf a \times \mathbf b} \mathbf c\right| = \left|\mathbf a\times\mathbf b\right| \frac{\left|\left(\mathbf a\times \mathbf b\right) \cdot \mathbf c\right|}{\left|\mathbf a\times \mathbf b\right|} = \left|\left(\mathbf a\times \mathbf b\right) \cdot \mathbf c\right|. \end{align} }[/math] The result follows.

An alternative representation of the volume uses geometric properties (angles and edge lengths) only:

[math]\displaystyle{ V = abc\sqrt{1+2\cos(\alpha)\cos(\beta)\cos(\gamma)-\cos^2(\alpha)-\cos^2(\beta)-\cos^2(\gamma)}, }[/math]

(V2)

where [math]\displaystyle{ \alpha = \angle(\mathbf b, \mathbf c) }[/math], [math]\displaystyle{ \beta = \angle(\mathbf a,\mathbf c) }[/math], [math]\displaystyle{ \gamma = \angle(\mathbf a,\mathbf b) }[/math], and [math]\displaystyle{ a,b,c }[/math] are the edge lengths.

Proof of (V2)

The proof of (V2) uses properties of a determinant and the geometric interpretation of the dot product:

Let [math]\displaystyle{ M }[/math] be the 3×3-matrix, whose columns are the vectors [math]\displaystyle{ \mathbf a, \mathbf b, \mathbf c }[/math] (see above). Then the following is true: [math]\displaystyle{ \begin{align} V^2 &= \left(\det M\right)^2 = \det M \det M = \det M^\mathsf{T} \det M = \det (M^\mathsf{T} M) \\ &= \det \begin{bmatrix} \mathbf a\cdot \mathbf a & \mathbf a\cdot \mathbf b & \mathbf a\cdot \mathbf c \\ \mathbf b\cdot \mathbf a & \mathbf b\cdot \mathbf b & \mathbf b\cdot \mathbf c \\ \mathbf c\cdot \mathbf a & \mathbf c\cdot \mathbf b & \mathbf c\cdot \mathbf c \end{bmatrix} \\ &=\ a^2\left(b^2c^2 - b^2c^2\cos(\alpha)\right) \\ &\quad-ab\cos(\gamma)\left(ab\cos(\gamma)c^2-ac\cos(\beta)\;bc\cos(\alpha)\right) \\ &\quad+ac\cos(\beta)\left(ab\cos(\gamma)bc\cos(\alpha)-ac\cos(\beta)b^2\right) \\ &=\ a^2b^2c^2-a^2b^2c^2\cos(\alpha) \\ &\quad-a^2b^2c^2\cos^2(\gamma)+a^2b^2c^2\cos(\alpha)\cos(\beta)\cos(\gamma) \\ &\quad+a^2b^2c^2\cos(\alpha)\cos(\beta)\cos(\gamma)-a^2b^2c^2\cos(\beta) \\ &=\ a^2b^2c^2\left(1-\cos^2(\alpha)-\cos^2(\gamma)+\cos(\alpha)\cos(\beta)\cos(\gamma)+\cos(\alpha)\cos(\beta)\cos(\gamma)+\cos^2(\beta)\right) \\ &=\ a^2b^2c^2\;\left(1+2\cos(\alpha)\cos(\beta)\cos(\gamma)-\cos^2(\alpha)-\cos^2(\beta)-\cos^2(\gamma)\right). \end{align} }[/math]

(The last steps use [math]\displaystyle{ \mathbf a \cdot \mathbf a=a^2 }[/math], ..., [math]\displaystyle{ \mathbf a\cdot \mathbf b=ab\cos\gamma }[/math], [math]\displaystyle{ \mathbf a \cdot \mathbf c = ac\cos\beta }[/math], [math]\displaystyle{ \mathbf b\cdot \mathbf c=bc\cos\alpha }[/math], ...)

Corresponding tetrahedron

The volume of any tetrahedron that shares three converging edges of a parallelepiped is equal to one sixth of the volume of that parallelepiped (see proof).

Surface area

The surface area of a parallelepiped is the sum of the areas of the bounding parallelograms: [math]\displaystyle{ \begin{align} A &= 2 \cdot \left(|\mathbf a \times \mathbf b| + |\mathbf a \times \mathbf c| + |\mathbf b \times \mathbf c|\right) \\ &= 2\left(ab\sin\gamma+ bc\sin\alpha+ca\sin\beta\right). \end{align} }[/math] (For labeling: see previous section.)

Special cases by symmetry

Octahedral symmetry subgroup relations with inversion center

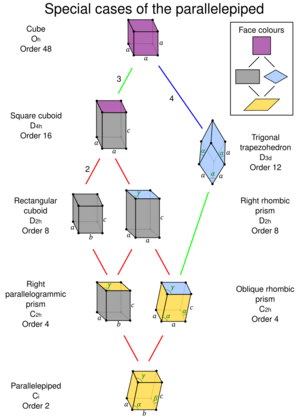Special cases of the parallelepiped

Form	Cube	Square cuboid	Trigonal trapezohedron	Rectangular cuboid	Right rhombic prism	Right parallelogrammic prism	Oblique rhombic prism
Constraints	[math]\displaystyle{ a=b=c }[/math] [math]\displaystyle{ \alpha=\beta=\gamma=90^\circ }[/math]	[math]\displaystyle{ a=b }[/math] [math]\displaystyle{ \alpha=\beta=\gamma=90^\circ }[/math]	[math]\displaystyle{ a=b=c }[/math] [math]\displaystyle{ \alpha=\beta=\gamma }[/math]	[math]\displaystyle{ \alpha=\beta=\gamma=90^\circ }[/math]	[math]\displaystyle{ a=b }[/math] [math]\displaystyle{ \alpha=\beta=90^\circ }[/math]	[math]\displaystyle{ \alpha=\beta=90^\circ }[/math]	[math]\displaystyle{ a=b }[/math] [math]\displaystyle{ \alpha=\beta }[/math]
Symmetry	Oh order 48	D4h order 16	D3d order 12	D2h order 8		C2h order 4
Image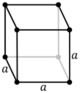
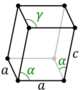
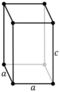
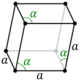
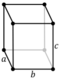
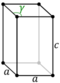
Faces	6 squares	2 squares, 4 rectangles	6 rhombi	6 rectangles	4 rectangles, 2 rhombi	4 rectangles, 2 parallelograms	2 rhombi, 4 parallelograms

• The parallelepiped with O_h symmetry is known as a cube, which has six congruent square faces.
• The parallelepiped with D_4h symmetry is known as a square cuboid, which has two square faces and four congruent rectangular faces.
• The parallelepiped with D_3d symmetry is known as a trigonal trapezohedron, which has six congruent rhombic faces (also called an isohedral rhombohedron).
• For parallelepipeds with D_2h symmetry, there are two cases:
  • Rectangular cuboid: it has six rectangular faces (also called a rectangular parallelepiped, or sometimes simply a cuboid).
  • Right rhombic prism: it has two rhombic faces and four congruent rectangular faces.

    Note: the fully rhombic special case, with two rhombic faces and four congruent square faces [math]\displaystyle{ (a=b=c) }[/math], has the same name, and the same symmetry group (D_2h , order 8).

• For parallelepipeds with C_2h symmetry, there are two cases:
  • Right parallelogrammic prism: it has four rectangular faces and two parallelogrammic faces.
  • Oblique rhombic prism: it has two rhombic faces, while of the other faces, two adjacent ones are equal and the other two also (the two pairs are each other's mirror image).

Perfect parallelepiped

A perfect parallelepiped is a parallelepiped with integer-length edges, face diagonals, and space diagonals. In 2009, dozens of perfect parallelepipeds were shown to exist, answering an open question of Richard Guy. One example has edges 271, 106, and 103, minor face diagonals 101, 266, and 255, major face diagonals 183, 312, and 323, and space diagonals 374, 300, 278, and 272.

Some perfect parallelepipeds having two rectangular faces are known. But it is not known whether there exist any with all faces rectangular; such a case would be called a perfect cuboid.

Parallelotope

Coxeter called the generalization of a parallelepiped in higher dimensions a parallelotope. In modern literature, the term parallelepiped is often used in higher (or arbitrary finite) dimensions as well.

Specifically in n-dimensional space it is called n-dimensional parallelotope, or simply n-parallelotope (or n-parallelepiped). Thus a parallelogram is a 2-parallelotope and a parallelepiped is a 3-parallelotope.

The diagonals of an n-parallelotope intersect at one point and are bisected by this point. Inversion in this point leaves the n-parallelotope unchanged. See also Fixed points of isometry groups in Euclidean space.

The edges radiating from one vertex of a k-parallelotope form a k-frame [math]\displaystyle{ (v_1,\ldots, v_n) }[/math] of the vector space, and the parallelotope can be recovered from these vectors, by taking linear combinations of the vectors, with weights between 0 and 1.

The n-volume of an n-parallelotope embedded in [math]\displaystyle{ \R^m }[/math] where [math]\displaystyle{ m \geq n }[/math] can be computed by means of the Gram determinant. Alternatively, the volume is the norm of the exterior product of the vectors: [math]\displaystyle{ V = \left\| v_1 \wedge \cdots \wedge v_n \right\| . }[/math]

If m = n, this amounts to the absolute value of the determinant of matrix formed by the components of the n vectors.

A formula to compute the volume of an n-parallelotope P in [math]\displaystyle{ \R^n }[/math], whose n + 1 vertices are [math]\displaystyle{ V_0,V_1, \ldots, V_n }[/math], is [math]\displaystyle{ \mathrm{Vol}(P) = \left|\det \left(\left[V_0\ 1\right]^\mathsf{T}, \left[V_1\ 1\right]^\mathsf{T}, \ldots, \left[V_n\ 1\right]^\mathsf{T}\right)\right|, }[/math] where [math]\displaystyle{ [V_i\ 1] }[/math] is the row vector formed by the concatenation of the components of [math]\displaystyle{ V_i }[/math] and 1.

Similarly, the volume of any n-simplex that shares n converging edges of a parallelotope has a volume equal to one 1/n! of the volume of that parallelotope.

Etymology

The term parallelepiped stems from Ancient Greek παραλληλεπίπεδον (parallēlepípedon, "body with parallel plane surfaces"), from parallēl ("parallel") + epípedon ("plane surface"), from epí- ("on") + pedon ("ground"). Thus the faces of a parallelepiped are planar, with opposite faces being parallel.

In English, the term parallelipipedon is attested in a 1570 translation of Euclid's Elements by Henry Billingsley. The spelling parallelepipedum is used in the 1644 edition of Pierre Hérigone's Cursus mathematicus. In 1663, the present-day parallelepiped is attested in Walter Charleton's Chorea gigantum.

Charles Hutton's Dictionary (1795) shows parallelopiped and parallelopipedon, showing the influence of the combining form parallelo-, as if the second element were pipedon rather than epipedon. Noah Webster (1806) includes the spelling parallelopiped. The 1989 edition of the Oxford English Dictionary describes parallelopiped (and parallelipiped) explicitly as incorrect forms, but these are listed without comment in the 2004 edition, and only pronunciations with the emphasis on the fifth syllable pi (/paɪ/) are given.

See also

• Lists of shapes

References

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 122, 1973. (He defines parallelotope as a generalization of a parallelogram and parallelepiped in n-dimensions.)

External links

• Weisstein, Eric W.. "Parallelepiped". http://mathworld.wolfram.com/Parallelepiped.html. 
• Weisstein, Eric W.. "Parallelotope". http://mathworld.wolfram.com/Parallelotope.html. 
• Paper model parallelepiped (net)