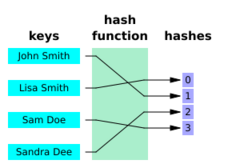
Perfect hash function

Short description: Hash function without any collisions

A perfect hash function for the four names shown

A minimal perfect hash function for the four names shown

In computer science, a perfect hash function h for a set S is a hash function that maps distinct elements in S to a set of m integers, with no collisions. In mathematical terms, it is an injective function.

Perfect hash functions may be used to implement a lookup table with constant worst-case access time. A perfect hash function can, as any hash function, be used to implement hash tables, with the advantage that no collision resolution has to be implemented. In addition, if the keys are not in the data and if it is known that queried keys will be valid, then the keys do not need to be stored in the lookup table, saving space.

Disadvantages of perfect hash functions are that S needs to be known for the construction of the perfect hash function. Non-dynamic perfect hash functions need to be re-constructed if S changes. For frequently changing S dynamic perfect hash functions may be used at the cost of additional space. The space requirement to store the perfect hash function is in O(n) where n is the number of keys in the structure.

The important performance parameters for perfect hash functions are the evaluation time, which should be constant, the construction time, and the representation size.

Application

A perfect hash function with values in a limited range can be used for efficient lookup operations, by placing keys from S (or other associated values) in a lookup table indexed by the output of the function. One can then test whether a key is present in S, or look up a value associated with that key, by looking for it at its cell of the table. Each such lookup takes constant time in the worst case. With perfect hashing, the associated data can be read or written with a single access to the table.

Performance of perfect hash functions

The important performance parameters for perfect hashing are the representation size, the evaluation time, the construction time, and additionally the range requirement [math]\displaystyle{ \frac{m}{n} }[/math] (average number of buckets per key in the hash table). The evaluation time can be as fast as O(1), which is optimal. The construction time needs to be at least O(n), because each element in S needs to be considered, and S contains n elements. This lower bound can be achieved in practice.

The lower bound for the representation size depends on m and n. Let m = (1+ε) n and h a perfect hash function. A good approximation for the lower bound is [math]\displaystyle{ \log e - \varepsilon \log \frac{1+\varepsilon}{\varepsilon} }[/math] Bits per element. For minimal perfect hashing, ε = 0, the lower bound is log e ≈ 1.44 bits per element.

Construction

A perfect hash function for a specific set S that can be evaluated in constant time, and with values in a small range, can be found by a randomized algorithm in a number of operations that is proportional to the size of S. The original construction of (Fredman Komlós) uses a two-level scheme to map a set S of n elements to a range of O(n) indices, and then map each index to a range of hash values. The first level of their construction chooses a large prime p (larger than the size of the universe from which S is drawn), and a parameter k, and maps each element x of S to the index

[math]\displaystyle{ g(x)=(kx\bmod p)\bmod n. }[/math]

If k is chosen randomly, this step is likely to have collisions, but the number of elements n_i that are simultaneously mapped to the same index i is likely to be small. The second level of their construction assigns disjoint ranges of O(n_i²) integers to each index i. It uses a second set of linear modular functions, one for each index i, to map each member x of S into the range associated with g(x).

As (Fredman Komlós) show, there exists a choice of the parameter k such that the sum of the lengths of the ranges for the n different values of g(x) is O(n). Additionally, for each value of g(x), there exists a linear modular function that maps the corresponding subset of S into the range associated with that value. Both k, and the second-level functions for each value of g(x), can be found in polynomial time by choosing values randomly until finding one that works.

The hash function itself requires storage space O(n) to store k, p, and all of the second-level linear modular functions. Computing the hash value of a given key x may be performed in constant time by computing g(x), looking up the second-level function associated with g(x), and applying this function to x. A modified version of this two-level scheme with a larger number of values at the top level can be used to construct a perfect hash function that maps S into a smaller range of length n + o(n).

A more recent method for constructing a perfect hash function is described by (Belazzougui Botelho) as "hash, displace, and compress". Here a first-level hash function g is also used to map elements onto a range of r integers. An element x ∈ S is stored in the Bucket B_g(x).

Then, in descending order of size, each bucket's elements are hashed by a hash function of a sequence of independent fully random hash functions (Φ₁, Φ₂, Φ₃, ...), starting with Φ₁. If the hash function does not produce any collisions for the bucket, and the resulting values are not yet occupied by other elements from other buckets, the function is chosen for that bucket. If not, the next hash function in the sequence is tested.

To evaluate the perfect hash function h(x) one only has to save the mapping σ of the bucket index g(x) onto the correct hash function in the sequence, resulting in h(x) = Φ_σ(g(x)).

Finally, to reduce the representation size, the (σ(i))_{0 ≤ i < r} are compressed into a form that still allows the evaluation in O(1).

This approach needs linear time in n for construction, and constant evaluation time. The representation size is in O(n), and depends on the achieved range. For example, with m = 1.23n (Belazzougui Botelho) achieved a representation size between 3.03 bits/key and 1.40 bits/key for their given example set of 10 million entries, with lower values needing a higher computation time. The space lower bound in this scenario is 0.88 bits/key.

Pseudocode

algorithm hash, displace, and compress is
(1) Split S into buckets Bi := g−1({i})∩S,0 ≤ i < r
(2) Sort buckets Bi in falling order according to size |Bi|
(3) Initialize array T[0...m-1] with 0's
(4) for all i ∈[r], in the order from (2), do
(5)     for l ← 1,2,...
(6)         repeat forming Ki ← {Φl(x)|x ∈ Bi}
(6)         until |Ki|=|Bi| and Ki∩{j|T[j]=1}= ∅
(7)     let σ(i):= the successful l
(8)     for all j ∈ Ki let T[j]:= 1
(9) Transform (σi)0≤i<r into compressed form, retaining O(1) access.

Space lower bounds

The use of O(n) words of information to store the function of (Fredman Komlós) is near-optimal: any perfect hash function that can be calculated in constant time requires at least a number of bits that is proportional to the size of S.

For minimal perfect hash functions the information theoretic space lower bound is

[math]\displaystyle{ \log_2e\approx1.44 }[/math]

bits/key.

For perfect hash functions, it is first assumed that the range of h is bounded by n as m = (1+ε) n. With the formula given by (Belazzougui Botelho) and for a universe [math]\displaystyle{ U\supseteq S }[/math] whose size |U| = u tends towards infinity, the space lower bounds is

[math]\displaystyle{ \log_2e-\varepsilon \log\frac{1+\varepsilon}{\varepsilon} }[/math]

bits/key, minus log(n) bits overall.

Extensions

Memory address identity

A trivial but pervasive example of perfect hashing is implicit in the (virtual) memory address space of a computer. Since each byte of virtual memory is a distinct, unique, directly addressable storage location, the value of the starting address where any object is stored in memory can be considered a de facto perfect hash of that object into the entire memory address range.

Dynamic perfect hashing

Using a perfect hash function is best in situations where there is a frequently queried large set, S, which is seldom updated. This is because any modification of the set S may cause the hash function to no longer be perfect for the modified set. Solutions which update the hash function any time the set is modified are known as dynamic perfect hashing, but these methods are relatively complicated to implement.

Minimal perfect hash function

A minimal perfect hash function is a perfect hash function that maps n keys to n consecutive integers – usually the numbers from 0 to n − 1 or from 1 to n. A more formal way of expressing this is: Let j and k be elements of some finite set S. Then h is a minimal perfect hash function if and only if h(j) = h(k) implies j = k (injectivity) and there exists an integer a such that the range of h is a..a + |S| − 1. It has been proven that a general purpose minimal perfect hash scheme requires at least [math]\displaystyle{ \log_2 e \approx 1.44 }[/math] bits/key. Assuming that [math]\displaystyle{ S }[/math] is a set of size [math]\displaystyle{ n }[/math] containing integers in the range [math]\displaystyle{ [1, 2^{o(n)}] }[/math], it is known how to efficiently construct an explicit minimal perfect hash function from [math]\displaystyle{ S }[/math] to [math]\displaystyle{ \{1, 2, \ldots, n\} }[/math] that uses space [math]\displaystyle{ n \log_2 e + o(n) }[/math]bits and that supports constant evaluation time. In practice, there are minimal perfect hashing schemes that use roughly 1.56 bits/key if given enough time.

k-perfect hashing

A hash function is k-perfect if at most k elements from S are mapped onto the same value in the range. The "hash, displace, and compress" algorithm can be used to construct k-perfect hash functions by allowing up to k collisions. The changes necessary to accomplish this are minimal, and are underlined in the adapted pseudocode below:

(4) for all i ∈[r], in the order from (2), do
(5)     for l ← 1,2,...
(6)         repeat forming Ki ← {Φl(x)|x ∈ Bi}
(6)         until |Ki|=|Bi| and Ki∩{j|T[j]=k}= ∅
(7)     let σ(i):= the successful l
(8)     for all j ∈ Ki set T[j]←T[j]+1

Order preservation

A minimal perfect hash function F is order preserving if keys are given in some order a₁, a₂, ..., a_n and for any keys a_j and a_k, j < k implies F(a_j) < F(a_k). In this case, the function value is just the position of each key in the sorted ordering of all of the keys. A simple implementation of order-preserving minimal perfect hash functions with constant access time is to use an (ordinary) perfect hash function to store a lookup table of the positions of each key. This solution uses [math]\displaystyle{ O(n \log n) }[/math] bits, which is optimal in the setting where the comparison function for the keys may be arbitrary. However, if the keys a₁, a₂, ..., a_n are integers drawn from a universe [math]\displaystyle{ \{1, 2, \ldots, U\} }[/math], then it is possible to construct an order-preserving hash function using only [math]\displaystyle{ O(n \log \log \log U) }[/math] bits of space. Moreover, this bound is known to be optimal.

Related constructions

While well-dimensioned hash tables have amortized average O(1) time (amortized average constant time) for lookups, insertions, and deletion, most hash table algorithms suffer from possible worst-case times that take much longer. A worst-case O(1) time (constant time even in the worst case) would be better for many applications (including network router and memory caches).

Few hash table algorithms support worst-case O(1) lookup time (constant lookup time even in the worst case). The few that do include: perfect hashing; dynamic perfect hashing; cuckoo hashing; hopscotch hashing; and extendible hashing.

A simple alternative to perfect hashing, which also allows dynamic updates, is cuckoo hashing. This scheme maps keys to two or more locations within a range (unlike perfect hashing which maps each key to a single location) but does so in such a way that the keys can be assigned one-to-one to locations to which they have been mapped. Lookups with this scheme are slower, because multiple locations must be checked, but nevertheless take constant worst-case time.

Further reading

• Richard J. Cichelli. Minimal Perfect Hash Functions Made Simple, Communications of the ACM, Vol. 23, Number 1, January 1980.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Third Edition. MIT Press, 2009. ISBN:978-0262033848. Section 11.5: Perfect hashing, pp. 267, 277–282.
• Fabiano C. Botelho, Rasmus Pagh and Nivio Ziviani. "Perfect Hashing for Data Management Applications".
• Fabiano C. Botelho and Nivio Ziviani. "External perfect hashing for very large key sets". 16th ACM Conference on Information and Knowledge Management (CIKM07), Lisbon, Portugal, November 2007.
• Djamal Belazzougui, Paolo Boldi, Rasmus Pagh, and Sebastiano Vigna. "Monotone minimal perfect hashing: Searching a sorted table with O(1) accesses". In Proceedings of the 20th Annual ACM-SIAM Symposium On Discrete Mathematics (SODA), New York, 2009. ACM Press.
• Marshall D. Brain and Alan L. Tharp. "Near-perfect Hashing of Large Word Sets". Software—Practice and Experience, vol. 19(10), 967-078, October 1989. John Wiley & Sons.
• Douglas C. Schmidt, GPERF: A Perfect Hash Function Generator, C++ Report, SIGS, Vol. 10, No. 10, November/December, 1998.

External links

• gperf is an Open Source C and C++ perfect hash generator (very fast, but only works for small sets)
• Minimal Perfect Hashing (bob algorithm) by Bob Jenkins
• cmph: C Minimal Perfect Hashing Library, open source implementations for many (minimal) perfect hashes (works for big sets)
• Sux4J: open source monotone minimal perfect hashing in Java
• MPHSharp: perfect hashing methods in C#
• BBHash: minimal perfect hash function in header-only C++
• Perfect::Hash, perfect hash generator in Perl that makes C code. Has a "prior art" section worth looking at.