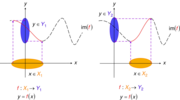Injective function
| Function | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x ↦ f (x) | |||||||||||||||||||||||||||||||||
| Examples by domain and codomain | |||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| Classes/properties | |||||||||||||||||||||||||||||||||
| Constant · Identity · Linear · Polynomial · Rational · Algebraic · Analytic · Smooth · Continuous · Measurable · Injective · Surjective · Bijective | |||||||||||||||||||||||||||||||||
| Constructions | |||||||||||||||||||||||||||||||||
| Restriction · Composition · λ · Inverse | |||||||||||||||||||||||||||||||||
| Generalizations | |||||||||||||||||||||||||||||||||
| Partial · Multivalued · Implicit | |||||||||||||||||||||||||||||||||
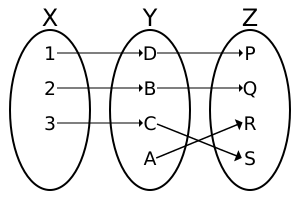
In mathematics, an injective function (also known as injection, or one-to-one function[1] ) is a function f that maps distinct elements of its domain to distinct elements; that is, x1 ≠ x2 implies f(x1) Template:≠ f(x2). (Equivalently, f(x1) = f(x2) implies x1 = x2 in the equivalent contrapositive statement.) In other words, every element of the function's codomain is the image of at most one element of its domain.[2] The term one-to-one function must not be confused with one-to-one correspondence that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain.
A homomorphism between algebraic structures is a function that is compatible with the operations of the structures. For all common algebraic structures, and, in particular for vector spaces, an injective homomorphism is also called a monomorphism. However, in the more general context of category theory, the definition of a monomorphism differs from that of an injective homomorphism.[3] This is thus a theorem that they are equivalent for algebraic structures; see Homomorphism § Monomorphism for more details.
A function [math]\displaystyle{ f }[/math] that is not injective is sometimes called many-to-one.[2]
Definition
thumb|An injective function, which is not also surjective Let [math]\displaystyle{ f }[/math] be a function whose domain is a set [math]\displaystyle{ X. }[/math] The function [math]\displaystyle{ f }[/math] is said to be injective provided that for all [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] in [math]\displaystyle{ X, }[/math] if [math]\displaystyle{ f(a) = f(b), }[/math] then [math]\displaystyle{ a = b }[/math]; that is, [math]\displaystyle{ f(a) = f(b) }[/math] implies [math]\displaystyle{ a=b. }[/math] Equivalently, if [math]\displaystyle{ a \neq b, }[/math] then [math]\displaystyle{ f(a) \neq f(b) }[/math] in the contrapositive statement.
Symbolically,[math]\displaystyle{ \forall a,b \in X, \;\; f(a)=f(b) \Rightarrow a=b, }[/math] which is logically equivalent to the contrapositive,[4][math]\displaystyle{ \forall a, b \in X, \;\; a \neq b \Rightarrow f(a) \neq f(b). }[/math]
Examples
For visual examples, readers are directed to the gallery section.
- For any set [math]\displaystyle{ X }[/math] and any subset [math]\displaystyle{ S \subseteq X, }[/math] the inclusion map [math]\displaystyle{ S \to X }[/math] (which sends any element [math]\displaystyle{ s \in S }[/math] to itself) is injective. In particular, the identity function [math]\displaystyle{ X \to X }[/math] is always injective (and in fact bijective).
- If the domain of a function is the empty set, then the function is the empty function, which is injective.
- If the domain of a function has one element (that is, it is a singleton set), then the function is always injective.
- The function [math]\displaystyle{ f : \R \to \R }[/math] defined by [math]\displaystyle{ f(x) = 2 x + 1 }[/math] is injective.
- The function [math]\displaystyle{ g : \R \to \R }[/math] defined by [math]\displaystyle{ g(x) = x^2 }[/math] is not injective, because (for example) [math]\displaystyle{ g(1) = 1 = g(-1). }[/math] However, if [math]\displaystyle{ g }[/math] is redefined so that its domain is the non-negative real numbers [0,+∞), then [math]\displaystyle{ g }[/math] is injective.
- The exponential function [math]\displaystyle{ \exp : \R \to \R }[/math] defined by [math]\displaystyle{ \exp(x) = e^x }[/math] is injective (but not surjective, as no real value maps to a negative number).
- The natural logarithm function [math]\displaystyle{ \ln : (0, \infty) \to \R }[/math] defined by [math]\displaystyle{ x \mapsto \ln x }[/math] is injective.
- The function [math]\displaystyle{ g : \R \to \R }[/math] defined by [math]\displaystyle{ g(x) = x^n - x }[/math] is not injective, since, for example, [math]\displaystyle{ g(0) = g(1) = 0. }[/math]
More generally, when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are both the real line [math]\displaystyle{ \R, }[/math] then an injective function [math]\displaystyle{ f : \R \to \R }[/math] is one whose graph is never intersected by any horizontal line more than once. This principle is referred to as the horizontal line test.[2]
Injections can be undone
Functions with left inverses are always injections. That is, given [math]\displaystyle{ f : X \to Y, }[/math] if there is a function [math]\displaystyle{ g : Y \to X }[/math] such that for every [math]\displaystyle{ x \in X }[/math], [math]\displaystyle{ g(f(x)) = x }[/math], then [math]\displaystyle{ f }[/math] is injective. In this case, [math]\displaystyle{ g }[/math] is called a retraction of [math]\displaystyle{ f. }[/math] Conversely, [math]\displaystyle{ f }[/math] is called a section of [math]\displaystyle{ g. }[/math]
Conversely, every injection [math]\displaystyle{ f }[/math] with a non-empty domain has a left inverse [math]\displaystyle{ g }[/math]. It can be defined by choosing an element [math]\displaystyle{ a }[/math] in the domain of [math]\displaystyle{ f }[/math] and setting [math]\displaystyle{ g(y) }[/math] to the unique element of the pre-image [math]\displaystyle{ f^{-1}[y] }[/math] (if it is non-empty) or to [math]\displaystyle{ a }[/math] (otherwise).[5]
The left inverse [math]\displaystyle{ g }[/math] is not necessarily an inverse of [math]\displaystyle{ f, }[/math] because the composition in the other order, [math]\displaystyle{ f \circ g, }[/math] may differ from the identity on [math]\displaystyle{ Y. }[/math] In other words, an injective function can be "reversed" by a left inverse, but is not necessarily invertible, which requires that the function is bijective.
Injections may be made invertible
In fact, to turn an injective function [math]\displaystyle{ f : X \to Y }[/math] into a bijective (hence invertible) function, it suffices to replace its codomain [math]\displaystyle{ Y }[/math] by its actual range [math]\displaystyle{ J = f(X). }[/math] That is, let [math]\displaystyle{ g : X \to J }[/math] such that [math]\displaystyle{ g(x) = f(x) }[/math] for all [math]\displaystyle{ x \in X }[/math]; then [math]\displaystyle{ g }[/math] is bijective. Indeed, [math]\displaystyle{ f }[/math] can be factored as [math]\displaystyle{ \operatorname{In}_{J,Y} \circ g, }[/math] where [math]\displaystyle{ \operatorname{In}_{J,Y} }[/math] is the inclusion function from [math]\displaystyle{ J }[/math] into [math]\displaystyle{ Y. }[/math]
More generally, injective partial functions are called partial bijections.
Other properties
- If [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] are both injective then [math]\displaystyle{ f \circ g }[/math] is injective.
- If [math]\displaystyle{ g \circ f }[/math] is injective, then [math]\displaystyle{ f }[/math] is injective (but [math]\displaystyle{ g }[/math] need not be).
- [math]\displaystyle{ f : X \to Y }[/math] is injective if and only if, given any functions [math]\displaystyle{ g, }[/math] [math]\displaystyle{ h : W \to X }[/math] whenever [math]\displaystyle{ f \circ g = f \circ h, }[/math] then [math]\displaystyle{ g = h. }[/math] In other words, injective functions are precisely the monomorphisms in the category Set of sets.
- If [math]\displaystyle{ f : X \to Y }[/math] is injective and [math]\displaystyle{ A }[/math] is a subset of [math]\displaystyle{ X, }[/math] then [math]\displaystyle{ f^{-1}(f(A)) = A. }[/math] Thus, [math]\displaystyle{ A }[/math] can be recovered from its image [math]\displaystyle{ f(A). }[/math]
- If [math]\displaystyle{ f : X \to Y }[/math] is injective and [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are both subsets of [math]\displaystyle{ X, }[/math] then [math]\displaystyle{ f(A \cap B) = f(A) \cap f(B). }[/math]
- Every function [math]\displaystyle{ h : W \to Y }[/math] can be decomposed as [math]\displaystyle{ h = f \circ g }[/math] for a suitable injection [math]\displaystyle{ f }[/math] and surjection [math]\displaystyle{ g. }[/math] This decomposition is unique up to isomorphism, and [math]\displaystyle{ f }[/math] may be thought of as the inclusion function of the range [math]\displaystyle{ h(W) }[/math] of [math]\displaystyle{ h }[/math] as a subset of the codomain [math]\displaystyle{ Y }[/math] of [math]\displaystyle{ h. }[/math]
- If [math]\displaystyle{ f : X \to Y }[/math] is an injective function, then [math]\displaystyle{ Y }[/math] has at least as many elements as [math]\displaystyle{ X, }[/math] in the sense of cardinal numbers. In particular, if, in addition, there is an injection from [math]\displaystyle{ Y }[/math] to [math]\displaystyle{ X, }[/math] then [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] have the same cardinal number. (This is known as the Cantor–Bernstein–Schroeder theorem.)
- If both [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are finite with the same number of elements, then [math]\displaystyle{ f : X \to Y }[/math] is injective if and only if [math]\displaystyle{ f }[/math] is surjective (in which case [math]\displaystyle{ f }[/math] is bijective).
- An injective function which is a homomorphism between two algebraic structures is an embedding.
- Unlike surjectivity, which is a relation between the graph of a function and its codomain, injectivity is a property of the graph of the function alone; that is, whether a function [math]\displaystyle{ f }[/math] is injective can be decided by only considering the graph (and not the codomain) of [math]\displaystyle{ f. }[/math]
Proving that functions are injective
A proof that a function [math]\displaystyle{ f }[/math] is injective depends on how the function is presented and what properties the function holds. For functions that are given by some formula there is a basic idea. We use the definition of injectivity, namely that if [math]\displaystyle{ f(x) = f(y), }[/math] then [math]\displaystyle{ x = y. }[/math][6]
Here is an example: [math]\displaystyle{ f(x) = 2 x + 3 }[/math]
Proof: Let [math]\displaystyle{ f : X \to Y. }[/math] Suppose [math]\displaystyle{ f(x) = f(y). }[/math] So [math]\displaystyle{ 2 x + 3 = 2 y + 3 }[/math] implies [math]\displaystyle{ 2 x = 2 y, }[/math] which implies [math]\displaystyle{ x = y. }[/math] Therefore, it follows from the definition that [math]\displaystyle{ f }[/math] is injective.
There are multiple other methods of proving that a function is injective. For example, in calculus if [math]\displaystyle{ f }[/math] is a differentiable function defined on some interval, then it is sufficient to show that the derivative is always positive or always negative on that interval. In linear algebra, if [math]\displaystyle{ f }[/math] is a linear transformation it is sufficient to show that the kernel of [math]\displaystyle{ f }[/math] contains only the zero vector. If [math]\displaystyle{ f }[/math] is a function with finite domain it is sufficient to look through the list of images of each domain element and check that no image occurs twice on the list.
A graphical approach for a real-valued function [math]\displaystyle{ f }[/math] of a real variable [math]\displaystyle{ x }[/math] is the horizontal line test. If every horizontal line intersects the curve of [math]\displaystyle{ f(x) }[/math] in at most one point, then [math]\displaystyle{ f }[/math] is injective or one-to-one.
Gallery
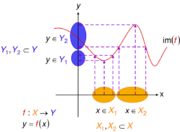
Not an injective function. Here [math]\displaystyle{ X_1 }[/math] and [math]\displaystyle{ X_2 }[/math] are subsets of [math]\displaystyle{ X, Y_1 }[/math] and [math]\displaystyle{ Y_2 }[/math] are subsets of [math]\displaystyle{ Y }[/math]: for two regions where the function is not injective because more than one domain element can map to a single range element. That is, it is possible for more than one [math]\displaystyle{ x }[/math] in [math]\displaystyle{ X }[/math] to map to the same [math]\displaystyle{ y }[/math] in [math]\displaystyle{ Y. }[/math]
Making functions injective. The previous function [math]\displaystyle{ f : X \to Y }[/math] can be reduced to one or more injective functions (say) [math]\displaystyle{ f : X_1 \to Y_1 }[/math] and [math]\displaystyle{ f : X_2 \to Y_2, }[/math] shown by solid curves (long-dash parts of initial curve are not mapped to anymore). Notice how the rule [math]\displaystyle{ f }[/math] has not changed – only the domain and range. [math]\displaystyle{ X_1 }[/math] and [math]\displaystyle{ X_2 }[/math] are subsets of [math]\displaystyle{ X, Y_1 }[/math] and [math]\displaystyle{ Y_2 }[/math] are subsets of [math]\displaystyle{ Y }[/math]: for two regions where the initial function can be made injective so that one domain element can map to a single range element. That is, only one [math]\displaystyle{ x }[/math] in [math]\displaystyle{ X }[/math] maps to one [math]\displaystyle{ y }[/math] in [math]\displaystyle{ Y. }[/math]
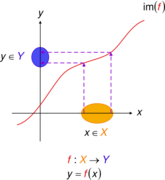
Injective functions. Diagramatic interpretation in the Cartesian plane, defined by the mapping [math]\displaystyle{ f : X \to Y, }[/math] where [math]\displaystyle{ y = f(x), }[/math] [math]\displaystyle{ X = }[/math] domain of function, [math]\displaystyle{ Y = }[/math] range of function, and [math]\displaystyle{ \operatorname{im}(f) }[/math] denotes image of [math]\displaystyle{ f. }[/math] Every one [math]\displaystyle{ x }[/math] in [math]\displaystyle{ X }[/math] maps to exactly one unique [math]\displaystyle{ y }[/math] in [math]\displaystyle{ Y. }[/math] The circled parts of the axes represent domain and range sets— in accordance with the standard diagrams above
See also
- Bijection, injection and surjection – Properties of mathematical functions
- Injective metric space – Type of metric space
- Monotonic function – Order-preserving mathematical function
- Univalent function
Notes
- ↑ Sometimes one-one function, in Indian mathematical education. "Chapter 1:Relations and functions". https://ncert.nic.in/ncerts/l/lemh101.pdf.
- ↑ 2.0 2.1 2.2 "Injective, Surjective and Bijective". https://www.mathsisfun.com/sets/injective-surjective-bijective.html.
- ↑ "Section 7.3 (00V5): Injective and surjective maps of presheaves—The Stacks project". https://stacks.math.columbia.edu/tag/00V5.
- ↑ Farlow, S. J.. "Injections, Surjections, and Bijections". http://www.math.umaine.edu/~farlow/sec42.pdf.
- ↑ Unlike the corresponding statement that every surjective function has a right inverse, this does not require the axiom of choice, as the existence of [math]\displaystyle{ a }[/math] is implied by the non-emptiness of the domain. However, this statement may fail in less conventional mathematics such as constructive mathematics. In constructive mathematics, the inclusion [math]\displaystyle{ \{ 0, 1 \} \to \R }[/math] of the two-element set in the reals cannot have a left inverse, as it would violate indecomposability, by giving a retraction of the real line to the set {0,1}.
- ↑ Williams, Peter. "Proving Functions One-to-One". http://www.math.csusb.edu/notes/proofs/bpf/node4.html.
References
- Bartle, Robert G. (1976), The Elements of Real Analysis (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-05464-1, p. 17 ff.
- Halmos, Paul R. (1974), Naive Set Theory, New York: Springer, ISBN 978-0-387-90092-6, p. 38 ff.
External links
- Earliest Uses of Some of the Words of Mathematics: entry on Injection, Surjection and Bijection has the history of Injection and related terms.
- Khan Academy – Surjective (onto) and Injective (one-to-one) functions: Introduction to surjective and injective functions
 |