Herman ring
In the mathematical discipline known as complex dynamics, the Herman ring is a Fatou component[1] where the rational function is conformally conjugate to an irrational rotation of the standard annulus.
Formal definition
Namely if ƒ possesses a Herman ring U with period p, then there exists a conformal mapping
- [math]\displaystyle{ \phi:U\rightarrow\{\zeta:0\lt r\lt |\zeta|\lt 1\} }[/math]
and an irrational number [math]\displaystyle{ \theta }[/math], such that
- [math]\displaystyle{ \phi\circ f^{\circ p}\circ\phi^{-1}(\zeta)=e^{2\pi i\theta}\zeta. }[/math]
So the dynamics on the Herman ring is simple.
Name
It was introduced by, and later named after, Michael Herman (1979[2]) who first found and constructed this type of Fatou component.
Function
- Polynomials do not have Herman rings.
- Rational functions can have Herman rings. According to the result of Shishikura, if a rational function ƒ possesses a Herman ring, then the degree of ƒ is at least 3.
- Transcendental entire maps do not have them[3]
- meromorphic functions can possess Herman rings. Herman rings for transcendental meromorphic functions have been studied by T. Nayak. According to a result of Nayak, if there is an omitted value for such a function then Herman rings of period 1 or 2 do not exist. Also, it is proved that if there is only a single pole and at least an omitted value, the function has no Herman ring of any period.
Examples
Herman and parabolic basin
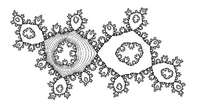
Here is an example of a rational function which possesses a Herman ring.[1]
- [math]\displaystyle{ f(z) = \frac{e^{2 \pi i \tau} z^2(z - 4)}{1 - 4z} }[/math]
where [math]\displaystyle{ \tau=0.6151732\dots }[/math] such that the rotation number of ƒ on the unit circle is [math]\displaystyle{ (\sqrt{5}-1)/2 }[/math].
The picture shown on the right is the Julia set of ƒ: the curves in the white annulus are the orbits of some points under the iterations of ƒ while the dashed line denotes the unit circle.
There is an example of rational function that possesses a Herman ring, and some periodic parabolic Fatou components at the same time.
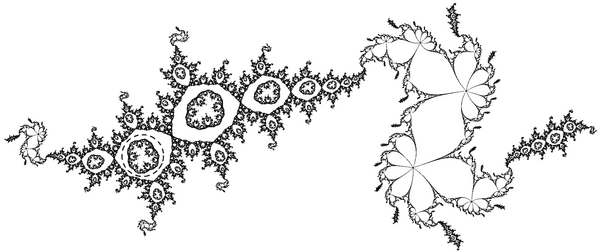
Period 2 Herman ring
Further, there is a rational function which possesses a Herman ring with period 2.
Here the expression of this rational function is
- [math]\displaystyle{ g_{a,b,c}(z) = \frac{z^2(z-a)}{z-b} + c, \, }[/math]
where
- [math]\displaystyle{ \begin{align} a & = 0.17021425+0.12612303i, \\ b & = 0.17115266+0.12592514i, \\ c & = -1.18521775-0.16885254i. \end{align} }[/math]
This example was constructed by quasiconformal surgery[4] from the quadratic polynomial
- [math]\displaystyle{ h(z)=z^2 - 1 - \frac{e^{\sqrt{5}\pi i}}{4} }[/math]
which possesses a Siegel disk with period 2. The parameters a, b, c are calculated by trial and error.
Letting
- [math]\displaystyle{ \begin{align} a & = 0.14285933+0.06404502i, \\ b & = 0.14362386+0.06461542i,\text{ and} \\ c & = -0.18242894-0.81957139i, \end{align} }[/math]
then the period of one of the Herman ring of ga,b,c is 3.
Shishikura also given an example:[5] a rational function which possesses a Herman ring with period 2, but the parameters showed above are different from his.
Period 5 Herman ring
So there is a question: How to find the formulas of the rational functions which possess Herman rings with higher period?
This question can be answered (for any period > 0) by using the Mandelbrot set for the rational functions ga,b,c. The classic Mandelbrot set (for quadratic polynomials) is approximated by iterating the critical point for each such polynomial, and identifying the polynomials for which the iterates of the critical point do not converge to infinity. Similarly a Mandelbrot set can be defined for the set of rational functions ga,b,c by distinguishing between the values of (a,b,c) in complex 3-space for which all the three critical points (i.e. points where the derivative vanishes) of the function converge to infinity, and the values whose critical points do not all converge to infinity.
For each value of a and b, the Mandelbrot set for ga,b,c can be calculated in the plane of complex values c. When a and b are nearly equal, this set approximates the classic Mandelbrot set for quadratic polynomials, because ga,b,c is equal to x2 + c when a=b. In the classic Mandelbrot set, Siegel discs can be approximated by choosing points along the edge of the Mandelbrot set with irrational winding number having continued fraction expansion with bounded denominators. The irrational numbers are of course only approximated in their computer representation. These denominators can be identified by the sequence of nodes along the edge of the Mandelbrot set approaching the point. Similarly, Herman rings can be identified in a Mandelbrot set of rational functions by observing a series of nodes arranged on both sides of a curve, and choosing points along that curve, avoiding the attached nodes, thereby obtaining a desired sequence of denominators in the continued fraction expansion of the rotation number. The following illustrates a planar slice of the Mandelbrot set of ga,b,c with |a-b| = .0001, and with c centered at a value of c which identifies a 5-cycle of Siegel discs in the classic Mandelbrot set.
The image above uses a =0.12601278 +.0458649i, b= .12582484 +.045796497i, and is centered at a value of c = 0.3688 -.3578, which is near 5-cycles of Siegel discs in the classic Mandelbrot set. In the above image, a 5-cycle of Herman rings can be approximated by choosing a point c along the above illustrated curve having nodes on both sides, for which ga,b,c has approximately the desired winding number, using values as follows:
[math]\displaystyle{ \begin{align} a & = .12601278 +.0458649i, \\ b & = .12582484 +.045796497i,\text{ and} \\ c & = 0.37144067 -.35829275i, \end{align} }[/math]
The resulting 5-cycle of Herman rings is illustrated below:
See also
References
- ↑ 1.0 1.1 John Milnor, Dynamics in one complex variable: Third Edition, Annals of Mathematics Studies, 160, Princeton Univ. Press, Princeton, NJ, 2006.
- ↑ Herman, Michael-Robert (1979), "Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations", Publications Mathématiques de l'IHÉS 49 (49): 5–233, doi:10.1007/BF02684798, ISSN 1618-1913, http://www.numdam.org/item?id=PMIHES_1979__49__5_0
- ↑ Omitted Values and Herman rings by Tarakanta Nayak.[full citation needed]
- ↑ Mitsuhiro Shishikura, On the quasiconformal surgery of rational functions. Ann. Sci. Ecole Norm. Sup. (4) 20 (1987), no. 1, 1–29.
- ↑ Mitsuhiro Shishikura, Surgery of complex analytic dynamical systems, in "Dynamical Systems and Nonlinear Oscillations", Ed. by Giko Ikegami, World Scientific Advanced Series in Dynamical Systems, 1, World Scientific, 1986, 93–105.
 |