Coulomb wave function
In mathematics, a Coulomb wave function is a solution of the Coulomb wave equation, named after Charles-Augustin de Coulomb. They are used to describe the behavior of charged particles in a Coulomb potential and can be written in terms of confluent hypergeometric functions or Whittaker functions of imaginary argument.
Coulomb wave equation
The Coulomb wave equation for a single charged particle of mass [math]\displaystyle{ m }[/math] is the Schrödinger equation with Coulomb potential[1]
- [math]\displaystyle{ \left(-\hbar^2\frac{\nabla^2}{2m}+\frac{Z \hbar c \alpha}{r}\right) \psi_{\vec{k}}(\vec{r}) = \frac{\hbar^2k^2}{2m} \psi_{\vec{k}}(\vec{r}) \,, }[/math]
where [math]\displaystyle{ Z=Z_1 Z_2 }[/math] is the product of the charges of the particle and of the field source (in units of the elementary charge, [math]\displaystyle{ Z=-1 }[/math] for the hydrogen atom), [math]\displaystyle{ \alpha }[/math] is the fine-structure constant, and [math]\displaystyle{ \hbar^2k^2/(2m) }[/math] is the energy of the particle. The solution, which is the Coulomb wave function, can be found by solving this equation in parabolic coordinates
- [math]\displaystyle{ \xi= r + \vec{r}\cdot\hat{k}, \quad \zeta= r - \vec{r}\cdot\hat{k} \qquad (\hat{k} = \vec{k}/k) \,. }[/math]
Depending on the boundary conditions chosen, the solution has different forms. Two of the solutions are[2][3]
- [math]\displaystyle{ \psi_{\vec{k}}^{(\pm)}(\vec{r}) = \Gamma(1\pm i\eta) e^{-\pi\eta/2} e^{i\vec{k}\cdot\vec{r}} M(\mp i\eta, 1, \pm ikr - i\vec{k}\cdot\vec{r}) \,, }[/math]
where [math]\displaystyle{ M(a,b,z) \equiv {}_1\!F_1(a;b;z) }[/math] is the confluent hypergeometric function, [math]\displaystyle{ \eta = Zmc\alpha/(\hbar k) }[/math] and [math]\displaystyle{ \Gamma(z) }[/math] is the gamma function. The two boundary conditions used here are
- [math]\displaystyle{ \psi_{\vec{k}}^{(\pm)}(\vec{r}) \rightarrow e^{i\vec{k}\cdot\vec{r}} \qquad (\vec{k}\cdot\vec{r} \rightarrow \pm\infty) \,, }[/math]
which correspond to [math]\displaystyle{ \vec{k} }[/math]-oriented plane-wave asymptotic states before or after its approach of the field source at the origin, respectively. The functions [math]\displaystyle{ \psi_{\vec{k}}^{(\pm)} }[/math] are related to each other by the formula
- [math]\displaystyle{ \psi_{\vec{k}}^{(+)} = \psi_{-\vec{k}}^{(-)*} \,. }[/math]
Partial wave expansion
The wave function [math]\displaystyle{ \psi_{\vec{k}}(\vec{r}) }[/math] can be expanded into partial waves (i.e. with respect to the angular basis) to obtain angle-independent radial functions [math]\displaystyle{ w_\ell(\eta,\rho) }[/math]. Here [math]\displaystyle{ \rho=kr }[/math].
- [math]\displaystyle{ \psi_{\vec{k}}(\vec{r}) = \frac{4\pi}{r} \sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell i^\ell w_{\ell}(\eta,\rho) Y_\ell^m (\hat{r}) Y_{\ell}^{m\ast} (\hat{k}) \,. }[/math]
A single term of the expansion can be isolated by the scalar product with a specific spherical harmonic
- [math]\displaystyle{ \psi_{k\ell m}(\vec{r}) = \int \psi_{\vec{k}}(\vec{r}) Y_\ell^m (\hat{k}) d\hat{k} = R_{k\ell}(r) Y_\ell^m(\hat{r}), \qquad R_{k\ell}(r) = 4\pi i^\ell w_\ell(\eta,\rho)/r. }[/math]
The equation for single partial wave [math]\displaystyle{ w_\ell(\eta,\rho) }[/math] can be obtained by rewriting the laplacian in the Coulomb wave equation in spherical coordinates and projecting the equation on a specific spherical harmonic [math]\displaystyle{ Y_\ell^m(\hat{r}) }[/math]
- [math]\displaystyle{ \frac{d^2 w_\ell}{d\rho^2}+\left(1-\frac{2\eta}{\rho}-\frac{\ell(\ell+1)}{\rho^2}\right)w_\ell=0 \,. }[/math]
The solutions are also called Coulomb (partial) wave functions or spherical Coulomb functions. Putting [math]\displaystyle{ z=-2i\rho }[/math] changes the Coulomb wave equation into the Whittaker equation, so Coulomb wave functions can be expressed in terms of Whittaker functions with imaginary arguments [math]\displaystyle{ M_{-i\eta,\ell+1/2}(-2i\rho) }[/math] and [math]\displaystyle{ W_{-i\eta,\ell+1/2}(-2i\rho) }[/math]. The latter can be expressed in terms of the confluent hypergeometric functions [math]\displaystyle{ M }[/math] and [math]\displaystyle{ U }[/math]. For [math]\displaystyle{ \ell\in\mathbb{Z} }[/math], one defines the special solutions [4]
- [math]\displaystyle{ H_\ell^{(\pm)}(\eta,\rho) = \mp 2i(-2)^{\ell}e^{\pi\eta/2} e^{\pm i \sigma_\ell}\rho^{\ell+1}e^{\pm i\rho}U(\ell+1\pm i\eta,2\ell+2,\mp 2i\rho) \,, }[/math]
where
- [math]\displaystyle{ \sigma_\ell = \arg \Gamma(\ell+1+i \eta) }[/math]
is called the Coulomb phase shift. One also defines the real functions
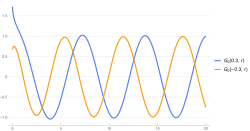
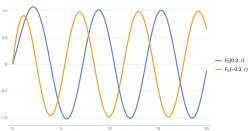
- [math]\displaystyle{ F_\ell(\eta,\rho) = \frac{1}{2i} \left(H_\ell^{(+)}(\eta,\rho)-H_\ell^{(-)}(\eta,\rho) \right) \,, }[/math]
- [math]\displaystyle{ G_\ell(\eta,\rho) = \frac{1}{2} \left(H_\ell^{(+)}(\eta,\rho)+H_\ell^{(-)}(\eta,\rho) \right) \,. }[/math]
In particular one has
- [math]\displaystyle{ F_\ell(\eta,\rho) = \frac{2^\ell e^{-\pi\eta/2}|\Gamma(\ell+1+i\eta)|}{(2\ell+1)!}\rho^{\ell+1}e^{i\rho}M(\ell+1+i\eta,2\ell+2,-2i\rho) \,. }[/math]
The asymptotic behavior of the spherical Coulomb functions [math]\displaystyle{ H_\ell^{(\pm)}(\eta,\rho) }[/math], [math]\displaystyle{ F_\ell(\eta,\rho) }[/math], and [math]\displaystyle{ G_\ell(\eta,\rho) }[/math] at large [math]\displaystyle{ \rho }[/math] is
- [math]\displaystyle{ H_\ell^{(\pm)}(\eta,\rho) \sim e^{\pm i \theta_\ell(\rho)} \,, }[/math]
- [math]\displaystyle{ F_\ell(\eta,\rho) \sim \sin \theta_\ell(\rho) \,, }[/math]
- [math]\displaystyle{ G_\ell(\eta,\rho) \sim \cos \theta_\ell(\rho) \,, }[/math]
where
- [math]\displaystyle{ \theta_\ell(\rho) = \rho - \eta \log(2\rho) -\frac{1}{2} \ell \pi + \sigma_\ell \,. }[/math]
The solutions [math]\displaystyle{ H_\ell^{(\pm)}(\eta,\rho) }[/math] correspond to incoming and outgoing spherical waves. The solutions [math]\displaystyle{ F_\ell(\eta,\rho) }[/math] and [math]\displaystyle{ G_\ell(\eta,\rho) }[/math] are real and are called the regular and irregular Coulomb wave functions. In particular one has the following partial wave expansion for the wave function [math]\displaystyle{ \psi_{\vec{k}}^{(+)}(\vec{r}) }[/math] [5]
- [math]\displaystyle{ \psi_{\vec{k}}^{(+)}(\vec{r}) = \frac{4\pi}{\rho} \sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell i^\ell e^{i \sigma_\ell} F_\ell(\eta,\rho) Y_\ell^m (\hat{r}) Y_{\ell}^{m\ast} (\hat{k}) \,, }[/math]
Properties of the Coulomb function
The radial parts for a given angular momentum are orthonormal. When normalized on the wave number scale (k-scale), the continuum radial wave functions satisfy [6][7]
- [math]\displaystyle{ \int_0^\infty R_{k\ell}^\ast(r) R_{k'\ell}(r) r^2 dr = \delta(k-k') }[/math]
Other common normalizations of continuum wave functions are on the reduced wave number scale ([math]\displaystyle{ k/2\pi }[/math]-scale),
- [math]\displaystyle{ \int_0^\infty R_{k\ell}^\ast(r) R_{k'\ell}(r) r^2 dr = 2\pi \delta(k-k') \,, }[/math]
and on the energy scale
- [math]\displaystyle{ \int_0^\infty R_{E\ell}^\ast(r) R_{E'\ell}(r) r^2 dr = \delta(E-E') \,. }[/math]
The radial wave functions defined in the previous section are normalized to
- [math]\displaystyle{ \int_0^\infty R_{k\ell}^\ast(r) R_{k'\ell}(r) r^2 dr = \frac{(2\pi)^3}{k^2} \delta(k-k') }[/math]
as a consequence of the normalization
- [math]\displaystyle{ \int \psi^{\ast}_{\vec{k}}(\vec{r}) \psi_{\vec{k}'}(\vec{r}) d^3r = (2\pi)^3 \delta(\vec{k}-\vec{k}') \,. }[/math]
The continuum (or scattering) Coulomb wave functions are also orthogonal to all Coulomb bound states[8]
- [math]\displaystyle{ \int_0^\infty R_{k\ell}^\ast(r) R_{n\ell}(r) r^2 dr = 0 }[/math]
due to being eigenstates of the same hermitian operator (the hamiltonian) with different eigenvalues.
Further reading
- Bateman, Harry (1953), Higher transcendental functions, 1, McGraw-Hill, http://apps.nrbook.com/bateman/Vol1.pdf, retrieved 2011-07-30.
- Jaeger, J. C.; Hulme, H. R. (1935), "The Internal Conversion of γ -Rays with the Production of Electrons and Positrons", Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 148 (865): 708–728, doi:10.1098/rspa.1935.0043, ISSN 0080-4630, Bibcode: 1935RSPSA.148..708J
- Slater, Lucy Joan (1960), Confluent hypergeometric functions, Cambridge University Press.
References
- ↑ Hill, Robert N. (2006), Drake, Gordon, ed., Handbook of atomic, molecular and optical physics, Springer New York, pp. 153–155, doi:10.1007/978-0-387-26308-3, ISBN 978-0-387-20802-2, https://cds.cern.ch/record/882343
- ↑ Landau, L. D.; Lifshitz, E. M. (1977), Course of theoretical physics III: Quantum mechanics, Non-relativistic theory (3rd ed.), Pergamon Press, p. 569
- ↑ Messiah, Albert (1961), Quantum mechanics, North Holland Publ. Co., p. 485
- ↑ Gaspard, David (2018), "Connection formulas between Coulomb wave functions", J. Math. Phys. 59 (11): 112104, doi:10.1063/1.5054368
- ↑ Messiah, Albert (1961), Quantum mechanics, North Holland Publ. Co., p. 426
- ↑ Formánek, Jiří (2004) (in Czech), Introduction to quantum theory I (2nd ed.), Prague: Academia, pp. 128–130
- ↑ Landau, L. D.; Lifshitz, E. M. (1977), Course of theoretical physics III: Quantum mechanics, Non-relativistic theory (3rd ed.), Pergamon Press, pp. 121
- ↑ Landau, L. D.; Lifshitz, E. M. (1977), Course of theoretical physics III: Quantum mechanics, Non-relativistic theory (3rd ed.), Pergamon Press, pp. 668–669
 |