Physics:Fine-structure constant
| Approximate value of α |
|---|
| 0.0072973525628(6) |
| Value of 1/ α |
| 137.035999084(21) |
| Quantum field theory |
|---|
 |
| History |
In physics, the fine-structure constant, also known as the Sommerfeld constant, commonly denoted by α (the Greek letter alpha), is a fundamental physical constant which quantifies the strength of the electromagnetic interaction between elementary charged particles.
It is a dimensionless quantity, independent of the system of units used, which is related to the strength of the coupling of an elementary charge e with the electromagnetic field, by the formula 4πε0ħcα = e2. Its numerical value is approximately 0.0072973525693 ≃ 1/137.035999084, with a relative uncertainty of 1.5×10−10.[1][lower-alpha 1]
The constant was named by Arnold Sommerfeld, who introduced it in 1916[2] when extending the Bohr model of the atom. α quantified the gap in the fine structure of the spectral lines of the hydrogen atom, which had been measured precisely by Michelson and Morley in 1887.[lower-alpha 2]
Why the constant should have this value is not understood,[3] but there are a number of ways to measure its value.
Definition
In terms of other fundamental physical constants, α may be defined as:[4] where
- e is the elementary charge (1.602176634×10−19 C[5]);
- h is the Planck constant (6.62607015×10−34 J⋅s[6]);
- ħ is the reduced Planck constant, ħ = h/2π (6.62607015×10−34 J⋅Hz−1/2π)
- c is the speed of light (299792458 m/s[7]);
- ε0 is the electric constant (8.8541878128(13)×10−12 F⋅m−1[8]).
Since the 2019 redefinition of the SI base units, the only quantity in this list that does not have an exact value in SI units is the electric constant.
Alternative systems of units
The electrostatic CGS system implicitly sets 4πε0 = 1, as commonly found in older physics literature, where the expression of the fine-structure constant becomes
A nondimensionalised system commonly used in high energy physics sets where the expressions for the fine-structure constant becomes[9] As such, the fine-structure constant is just a quantity determining (or determined by) the elementary charge: e = √4πα ≈ 0.30282212 in terms of such a natural unit of charge.
In the system of Hartree atomic units, which sets e = me = ħ = 4πε0 = 1, the expression for the fine-structure constant becomes
Measurement

The 2018 CODATA recommended value of α is[1]
- α = e2/ 4πε0ħc = 0.0072973525693(11).
This has a relative standard uncertainty of 1.5×10−10.[1]
This value for α gives µ0 = 4π × 1.00000000054(15)×10−7 H⋅m−1, 3.6 standard deviations away from its old defined value, but with the mean differing from the old value by only 0.54 parts per billion.
Historically the value of the reciprocal of the fine-structure constant is often given. The 2018 CODATA recommended value is[10]
- 1/α = 137.035999084(21).
While the value of α can be determined from estimates of the constants that appear in any of its definitions, the theory of quantum electrodynamics (QED) provides a way to measure α directly using the quantum Hall effect or the anomalous magnetic moment of the electron.[11] Other methods include the A.C. Josephson effect and photon recoil in atom interferometry.[12] There is general agreement for the value of α, as measured by these different methods. The preferred methods in 2019 are measurements of electron anomalous magnetic moments and of photon recoil in atom interferometry.[12] The theory of QED predicts a relationship between the dimensionless magnetic moment of the electron and the fine-structure constant α (the magnetic moment of the electron is also referred to as the electron g-factor ge). One of the most precise values of α obtained experimentally (as of 2023) is based on a measurement of ge using a one-electron so-called "quantum cyclotron" apparatus,[11] together with a calculation via the theory of QED that involved 12672 tenth-order Feynman diagrams:[13]
- 1/α = 137.035999166(15).
This measurement of α has a relative standard uncertainty of 1.1×10−10. This value and uncertainty are about the same as the latest experimental results.[14]
Further refinement of the experimental value was published by the end of 2020, giving the value
- 1/α = 137.035999206(11),
with a relative accuracy of 8.1×10−11, which has a significant discrepancy from the previous experimental value.[15]
Physical interpretations
The fine-structure constant, α, has several physical interpretations. α is:
- The ratio of two energies:
- the energy needed to overcome the electrostatic repulsion between two electrons a distance of d apart, and
- the energy of a single photon of wavelength λ = 2πd (or of angular wavelength d; see Planck relation):
- The ratio of the velocity of the electron in the first circular orbit of the Bohr model of the atom, which is 1/4πε0e2/ħ, to the speed of light in vacuum, c.[16] This is Sommerfeld's original physical interpretation. Then the square of α is the ratio between the Hartree energy (27.2 eV = twice the Rydberg energy = approximately twice its ionization energy) and the electron rest energy (511 keV).
- is the ratio of the potential energy of the electron in the first circular orbit of the Bohr model of the atom and the energy equivalent to the mass of an electron. Using the Virial theorem in the Bohr model of the atom which means that Essentially this ratio follows from the electron's velocity being .
- The two ratios of three characteristic lengths: the classical electron radius re, the Compton wavelength of the electron λe, and the Bohr radius a0:
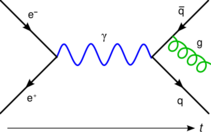
- In quantum electrodynamics, α is directly related to the coupling constant determining the strength of the interaction between electrons and photons.[17] The theory does not predict its value. Therefore, α must be determined experimentally. In fact, α is one of the empirical parameters in the Standard Model of particle physics, whose value is not determined within the Standard Model.
- In the electroweak theory unifying the weak interaction with electromagnetism, α is absorbed into two other coupling constants associated with the electroweak gauge fields. In this theory, the electromagnetic interaction is treated as a mixture of interactions associated with the electroweak fields. The strength of the electromagnetic interaction varies with the strength of the energy field.
- In the fields of electrical engineering and solid-state physics, the fine-structure constant is one fourth the product of the characteristic impedance of free space, and the conductance quantum, :
The optical conductivity of graphene for visible frequencies is theoretically given by π /4 G0 , and as a result its light absorption and transmission properties can be expressed in terms of the fine-structure constant alone.[18] The absorption value for normal-incident light on graphene in vacuum would then be given by πα/ (1 + πα/2)2 or 2.24%, and the transmission by 1/(1 + πα/2)2 or 97.75% (experimentally observed to be between 97.6% and 97.8%). The reflection would then be given by π2 α2/ 4 (1 + πα/2)2. - The fine-structure constant gives the maximum positive charge of an atomic nucleus that will allow a stable electron-orbit around it within the Bohr model (element feynmanium).[19] For an electron orbiting an atomic nucleus with atomic number Z the relation is mv2/r = 1/ 4πε0 Ze2/r2 . The Heisenberg uncertainty principle momentum/position uncertainty relationship of such an electron is just mvr = ħ. The relativistic limiting value for v is c, and so the limiting value for Z is the reciprocal of the fine-structure constant, 137.[20]
- The magnetic moment of the electron indicates that the charge is circulating at a radius rQ with the velocity of light.[21] It generates the radiation energy mec2 and has an angular momentum L = 1 ħ = rQmec. The field energy of the stationary Coulomb field is mec2 = e2/4πε0re and defines the classical electron radius re. These values inserted into the definition of alpha yields α = re/ rQ. It compares the dynamic structure of the electron with the classical static assumption.
- Given two hypothetical point particles each of Planck mass and elementary charge, separated by any distance, α is the ratio of their electrostatic repulsive force to their gravitational attractive force.
- The square of the ratio of the elementary charge to the Planck charge
When perturbation theory is applied to quantum electrodynamics, the resulting perturbative expansions for physical results are expressed as sets of power series in α. Because α is much less than one, higher powers of α are soon unimportant, making the perturbation theory practical in this case. On the other hand, the large value of the corresponding factors in quantum chromodynamics makes calculations involving the strong nuclear force extremely difficult.
Variation with energy scale
In quantum electrodynamics, the more thorough quantum field theory underlying the electromagnetic coupling, the renormalization group dictates how the strength of the electromagnetic interaction grows logarithmically as the relevant energy scale increases. The value of the fine-structure constant α is linked to the observed value of this coupling associated with the energy scale of the electron mass: the electron is a lower bound for this energy scale, because it (and the positron) is the lightest charged object whose quantum loops can contribute to the running. Therefore, 1/ 137.03600 is the asymptotic value of the fine-structure constant at zero energy. At higher energies, such as the scale of the Z boson, about 90 GeV, one instead measures an effective α ≈ 1/127.[22]
As the energy scale increases, the strength of the electromagnetic interaction in the Standard Model approaches that of the other two fundamental interactions, a feature important for grand unification theories. If quantum electrodynamics were an exact theory, the fine-structure constant would actually diverge at an energy known as the Landau pole – this fact undermines the consistency of quantum electrodynamics beyond perturbative expansions.
History

Based on the precise measurement of the hydrogen atom spectrum by Michelson and Morley in 1887,[lower-alpha 3] Sommerfeld extended the Bohr model to include elliptical orbits and relativistic dependence of mass on velocity. He introduced a term for the fine-structure constant in 1916.[lower-alpha 4] The first physical interpretation of the fine-structure constant α was as the ratio of the velocity of the electron in the first circular orbit of the relativistic Bohr atom to the speed of light in the vacuum.[26] Equivalently, it was the quotient between the minimum angular momentum allowed by relativity for a closed orbit, and the minimum angular momentum allowed for it by quantum mechanics. It appears naturally in Sommerfeld's analysis, and determines the size of the splitting or fine-structure of the hydrogenic spectral lines. This constant was not seen as significant until Paul Dirac's linear relativistic wave equation in 1928, which gave the exact fine structure formula.[27]: 407
With the development of quantum electrodynamics (QED) the significance of α has broadened from a spectroscopic phenomenon to a general coupling constant for the electromagnetic field, determining the strength of the interaction between electrons and photons. The term α/2π is engraved on the tombstone of one of the pioneers of QED, Julian Schwinger, referring to his calculation of the anomalous magnetic dipole moment.
History of measurements
Successive values determined for the fine-structure constant[28] Date α 1/α Sources 1969 Jul 0.007297351(11) 137.03602(21) CODATA 1969 1973 0.0072973461(81) 137.03612(15) CODATA 1973 1987 Jan 0.00729735308(33) 137.0359895(61) CODATA 1986 1998 0.007297352582(27) 137.03599883(51) Kinoshita 2000 Apr 0.007297352533(27) 137.03599976(50) CODATA 1998 2002 0.007297352568(24) 137.03599911(46) CODATA 2002 2007 Jul 0.0072973525700(52) 137.035999070(98) Gabrielse (2007) 2008 Jun 2 0.0072973525376(50) 137.035999679(94) CODATA 2006 2008 Jul 0.0072973525692(27) 137.035999084(51) Gabrielse (2008), Hanneke (2008) 2010 Dec 0.0072973525717(48) 137.035999037(91) Bouchendira (2010) 2011 Jun 0.0072973525698(24) 137.035999074(44) CODATA 2010 2015 Jun 25 0.0072973525664(17) 137.035999139(31) CODATA 2014 2017 Jul 10 0.0072973525657(18) 137.035999150(33) Aoyama et al. (2017)[29] 2018 Dec 12 0.0072973525713(14) 137.035999046(27) Parker, Yu, et al. (2018)[30] 2019 May 20 0.0072973525693(11) 137.035999084(21) CODATA 2018 2020 Dec 2 0.0072973525628(6) 137.035999206(11) Morel et al. (2020)[31] 2023 Feb 13 0.0072973525649(8) 137.035999166(15) Fan et al. (2023)[11]
The CODATA values in the above table are computed by averaging other measurements; they are not independent experiments.
Potential time-variation
Physicists have pondered whether the fine-structure constant is in fact constant, or whether its value differs by location and over time. A varying α has been proposed as a way of solving problems in cosmology and astrophysics.[32][33][34][35] String theory and other proposals for going beyond the Standard Model of particle physics have led to theoretical interest in whether the accepted physical constants (not just α) actually vary.
In the experiments below, Δα represents the change in α over time, which can be computed by αprev − αnow . If the fine-structure constant really is a constant, then any experiment should show that
or as close to zero as experiment can measure. Any value far away from zero would indicate that α does change over time. So far, most experimental data is consistent with α being constant.
Past rate of change
The first experimenters to test whether the fine-structure constant might actually vary examined the spectral lines of distant astronomical objects and the products of radioactive decay in the Oklo natural nuclear fission reactor. Their findings were consistent with no variation in the fine-structure constant between these two vastly separated locations and times.[36][37][38][39][40][41]
Improved technology at the dawn of the 21st century made it possible to probe the value of α at much larger distances and to a much greater accuracy. In 1999, a team led by John K. Webb of the University of New South Wales claimed the first detection of a variation in α.[42][43][44][45] Using the Keck telescopes and a data set of 128 quasars at redshifts 0.5 < z < 3, Webb et al. found that their spectra were consistent with a slight increase in α over the last 10–12 billion years. Specifically, they found that
In other words, they measured the value to be somewhere between −0.0000047 and −0.0000067. This is a very small value, but the error bars do not actually include zero. This result either indicates that α is not constant or that there is experimental error unaccounted for.
In 2004, a smaller study of 23 absorption systems by Chand et al., using the Very Large Telescope, found no measurable variation:[46][47]
However, in 2007 simple flaws were identified in the analysis method of Chand et al., discrediting those results.[48][49]
King et al. have used Markov chain Monte Carlo methods to investigate the algorithm used by the UNSW group to determine Δα/ α from the quasar spectra, and have found that the algorithm appears to produce correct uncertainties and maximum likelihood estimates for Δα/ α for particular models.[50] This suggests that the statistical uncertainties and best estimate for Δα/ α stated by Webb et al. and Murphy et al. are robust.
Lamoreaux and Torgerson analyzed data from the Oklo natural nuclear fission reactor in 2004, and concluded that α has changed in the past 2 billion years by 45 parts per billion. They claimed that this finding was "probably accurate to within 20%". Accuracy is dependent on estimates of impurities and temperature in the natural reactor. These conclusions have to be verified.[51][52][53][54]
In 2007, Khatri and Wandelt of the University of Illinois at Urbana-Champaign realized that the 21 cm hyperfine transition in neutral hydrogen of the early universe leaves a unique absorption line imprint in the cosmic microwave background radiation.[55] They proposed using this effect to measure the value of α during the epoch before the formation of the first stars. In principle, this technique provides enough information to measure a variation of 1 part in 109 (4 orders of magnitude better than the current quasar constraints). However, the constraint which can be placed on α is strongly dependent upon effective integration time, going as 1⁄√t . The European LOFAR radio telescope would only be able to constrain Δα/ α to about 0.3%.[55] The collecting area required to constrain Δα/ α to the current level of quasar constraints is on the order of 100 square kilometers, which is economically impracticable at the present time.
Present rate of change
In 2008, Rosenband et al.[56]
used the frequency ratio of Al+
and Hg+
in single-ion optical atomic clocks to place a very stringent constraint on the present-time temporal variation of α, namely Δα/ α = (−1.6±2.3)×10−17 per year. Note that any present day null constraint on the time variation of alpha does not necessarily rule out time variation in the past. Indeed, some theories[57]
that predict a variable fine-structure constant also predict that the value of the fine-structure constant should become practically fixed in its value once the universe enters its current dark energy-dominated epoch.
Spatial variation – Australian dipole
Researchers from Australia have said they had identified a variation of the fine-structure constant across the observable universe.[58][59][60] [61] [62] [63]
These results have not been replicated by other researchers. In September and October 2010, after Webb et al.'s released research, physicists C. Orzel and S.M. Carroll separately suggested various approaches of how Webb's observations may be wrong. Orzel argues[64] that the study may contain wrong data due to subtle differences in the two telescopes[65] a totally different approach; he looks at the fine-structure constant as a scalar field and claims that if the telescopes are correct and the fine-structure constant varies smoothly over the universe, then the scalar field must have a very small mass. However, previous research has shown that the mass is not likely to be extremely small. Both of these scientists' early criticisms point to the fact that different techniques are needed to confirm or contradict the results, a conclusion Webb, et al., previously stated in their study.[61]
Other research finds no meaningful variation in the fine structure constant.[66][67]
Anthropic explanation
The anthropic principle is an argument about the reason the fine-structure constant has the value it does: stable matter, and therefore life and intelligent beings, could not exist if its value were very different. α needs to be between around 1/180 and 1/85 to have proton decay to be slow enough for life to be possible.[68]
Numerological explanations and multiverse theory
As a dimensionless constant which does not seem to be directly related to any mathematical constant, the fine-structure constant has long fascinated physicists.
Arthur Eddington argued that the value could be "obtained by pure deduction" and he related it to the Eddington number, his estimate of the number of protons in the universe.[69] This led him in 1929 to conjecture that the reciprocal of the fine-structure constant was not approximately but precisely the integer 137.[70] By the 1940s experimental values for 1/ α deviated sufficiently from 137 to refute Eddington's arguments.[27]
Physicist Wolfgang Pauli commented on the appearance of certain numbers in physics, including fine-structure constant, which he noted approximates the prime number 137.[71] This constant so intrigued that he collaborated with psychoanalyst Carl Jung in a quest to understand its significance.[72] Similarly, Max Born believed that if the value of α differed, the universe would degenerate, and thus that α = 1/137 is a law of nature.[73][lower-alpha 5]
Richard Feynman, one of the originators and early developers of the theory of quantum electrodynamics (QED), referred to the fine-structure constant in these terms:
There is a most profound and beautiful question associated with the observed coupling constant, e – the amplitude for a real electron to emit or absorb a real photon. It is a simple number that has been experimentally determined to be close to 0.08542455. (My physicist friends won't recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with an uncertainty of about 2 in the last decimal place. It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.)
Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms? Nobody knows. It's one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by humans. You might say the "hand of God" wrote that number, and "we don't know how He pushed His pencil." We know what kind of a dance to do experimentally to measure this number very accurately, but we don't know what kind of dance to do on the computer to make this number come out – without putting it in secretly!
Conversely, statistician I. J. Good argued that a numerological explanation would only be acceptable if it could be based on a good theory that is not yet known but "exists" in the sense of a Platonic Ideal.[lower-alpha 6]
Attempts to find a mathematical basis for this dimensionless constant have continued up to the present time. However, no numerological explanation has ever been accepted by the physics community.
In the early 21st century, multiple physicists, including Stephen Hawking in his book A Brief History of Time, began exploring the idea of a multiverse, and the fine-structure constant was one of several universal constants that suggested the idea of a fine-tuned universe.[75]
Quotes
For historical reasons, α is known as the fine structure constant. Unfortunately, this name conveys a false impression. We have seen that the charge of an electron is not strictly constant but varies with distance because of quantum effects; hence α must be regarded as a variable, too. The value 1/137 is the asymptotic value of α shown in Fig. 1.5a.[76]
— Francis Halzen and Alan Martin (1984) [77]
The mystery about α is actually a double mystery: The first mystery – the origin of its numerical value α ≈ 1/137 – has been recognized and discussed for decades. The second mystery – the range of its domain – is generally unrecognized.
— M.H. MacGregor (2007)[78]
When I die my first question to the Devil will be: What is the meaning of the fine structure constant?
See also
- Dimensionless physical constant
- Electric constant
- Hyperfine structure
- Planck constant
- Speed of light
Footnotes
- ↑ CODATA 2018, published in May 2019, takes into accounts measurements published up to 2018. Morel et al. (2020) have claimed a measurement with a relative uncertainty below 10−10; their value is also significantly lower than the 2018 recommended value, to an agreement of merely 9×10−10.
- ↑ In quantum electrodynamics, α is proportional to the square of the coupling constant for a charged particle to the electromagnetic field. There are analogous coupling constants that give the interaction strength of the nuclear strong force and the nuclear weak force.
- ↑ "Among other substances [that were] tried in the preliminary experiments, were thallium, lithium, and hydrogen. ... It may be noted, that in [the] case of the red hydrogen line, the interference phenomena disappeared at about 15,000 wave-lengths, and again at about 45,000 wave-lengths: So that the red hydrogen line must be a double line with the components about one-sixtieth as distant as the sodium lines."[24](p430)
- ↑
"Wir fügen den Bohrschen Gleichungen (46) und (47) die charakteristische Konstante unserer Feinstrukturen hinzu, die zugleich mit der Kenntnis des Wasserstoffdubletts oder des Heliumtripletts in §10 oder irgend einer analogen Struktur bekannt ist."
Template:---
(We add, to Bohr's equations (46) and (47), the characteristic constant of our fine structures which is known at once from knowledge of the hydrogen doublet or the helium triplet in §10 or any analogous structure.) [25](p91) - ↑ If alpha were bigger than it really is, we should not be able to distinguish matter from ether [the vacuum, nothingness], and our task to disentangle the natural laws would be hopelessly difficult. The fact however that alpha has just its value 1/137 is certainly no chance but itself a law of nature. It is clear that the explanation of this number must be the central problem of natural philosophy. — Max Born[73]
- ↑ There have been a few examples of numerology that have led to theories that transformed society: See the mention of Kirchhoff and Balmer in Good (1962) p. 316 ... and one can well include Kepler on account of his third law. It would be fair enough to say that numerology was the origin of the theories of electromagnetism, quantum mechanics, gravitation. ... So I intend no disparagement when I describe a formula as numerological. When a numerological formula is proposed, then we may ask whether it is correct. ... I think an appropriate definition of correctness is that the formula has a good explanation, in a Platonic sense, that is, the explanation could be based on a good theory that is not yet known but 'exists' in the universe of possible reasonable ideas. — I.J. Good (1990)[74]
References
- ↑ 1.0 1.1 1.2 "2018 CODATA Value: fine-structure constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?alph. Retrieved 2019-05-20.
- ↑ Sommerfeld, Arnold (1916). "Zur Quantentheorie der Spektrallinien". Annalen der Physik 4 (51): 51–52. https://babel.hathitrust.org/cgi/pt?id=nyp.33433090771183&view=1up&seq=65. Retrieved 2020-12-06. Equation 12a, "rund 7·10−3" (about ...)
- ↑ 3.0 3.1 QED: The Strange Theory of Light and Matter. Princeton University Press. 1985. p. 129. ISBN 978-0-691-08388-9.
- ↑ Mohr, P. J.; Taylor, B. N.; Newell, D. B. (2019). "Fine-structure constant". CODATA Internationally recommended 2018 values of the fundamental physical constants. National Institute of Standards and Technology. https://physics.nist.gov/cgi-bin/cuu/Value?alph.
- ↑ "2018 CODATA Value: elementary charge". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?e. Retrieved 2019-05-20.
- ↑ "2018 CODATA Value: Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?h. Retrieved 2019-05-20.
- ↑ "2018 CODATA Value: speed of light in vacuum". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?c. Retrieved 2019-05-20.
- ↑ "2018 CODATA Value: vacuum electric permittivity". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?ep0. Retrieved 2019-05-20.
- ↑ Peskin, M.; Schroeder, D. (1995). An Introduction to Quantum Field Theory. Westview Press. p. 125. ISBN 978-0-201-50397-5. https://archive.org/details/introductiontoqu0000pesk/page/125.
- ↑ "2018 CODATA Value: inverse fine-structure constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?alphinv. Retrieved 2019-05-20.
- ↑ 11.0 11.1 11.2 Fan, X.; Myers, T. G.; Sukra, B. A. D.; Gabrielse, G. (2023-02-13). "Measurement of the Electron Magnetic Moment". Physical Review Letters 130 (7): 071801. doi:10.1103/PhysRevLett.130.071801. https://link.aps.org/doi/10.1103/PhysRevLett.130.071801.
- ↑ 12.0 12.1 Yu, C.; Zhong, W.; Estey, B.; Kwan, J.; Parker, R.H.; Müller, H. (2019). "Atom‐interferometry measurement of the fine structure constant". Annalen der Physik 531 (5): 1800346. doi:10.1002/andp.201800346. Bibcode: 2019AnP...53100346Y.
- ↑ Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. (2012). "Tenth-order QED contribution to the electron g − 2 and an improved value of the fine structure constant". Physical Review Letters 109 (11): 111807. doi:10.1103/PhysRevLett.109.111807. PMID 23005618. Bibcode: 2012PhRvL.109k1807A.
- ↑ Bouchendira, Rym; Cladé, Pierre; Guellati-Khélifa, Saïda; Nez, François; Biraben, François (2011). "New determination of the fine-structure constant and test of the quantum electrodynamics". Physical Review Letters 106 (8): 080801. doi:10.1103/PhysRevLett.106.080801. PMID 21405559. Bibcode: 2011PhRvL.106h0801B. https://hal.archives-ouvertes.fr/hal-00547525/file/MesureAlpha2010.pdf.
- ↑ Morel, Léo; Yao, Zhibin; Cladé, Pierre; Guellati-Khélifa, Saïda (2020). "Determination of the fine-structure constant with an accuracy of 81 parts per trillion". Nature 588 (7836): 61–65. doi:10.1038/s41586-020-2964-7. PMID 33268866. Bibcode: 2020Natur.588...61M. https://hal.archives-ouvertes.fr/hal-03107990/file/main.pdf.
- ↑ Atombau und Spektrallinien (2 ed.). Braunschweig, DE: Friedr. Vieweg & Sohn. 1921. p. 241-242, Equation 8. https://archive.org/stream/atombauundspekt00sommgoog?ref=ol#page/n261/mode/2up. "Das Verhältnis nennen wir α." English translation. Methuen & co.. 1923. https://babel.hathitrust.org/cgi/pt?id=mdp.39015078632786&view=1up&seq=233.
- ↑ Riazuddin, Fayyazuddin (2012). A Modern Introduction to Particle Physics (third ed.). World Scientific. pp. 4. ISBN 9789814338837. https://books.google.com/books?id=dbysnBTHF4QC. Retrieved 20 April 2017.
- ↑ Nair, R. R.; Blake, P.; Grigorenko, A. N.; Novoselov, K. S.; Booth, T. J.; Stauber, T.; Peres, N. M. R.; Geim, A. K. (2008). "Fine Structure Constant Defines Visual Transparency of Graphene". Science 320 (5881): 1308. doi:10.1126/science.1156965. PMID 18388259. Bibcode: 2008Sci...320.1308N.
- ↑ Chandrasekhar, S. (1 April 1984). "On stars, their evolution and their stability". Reviews of Modern Physics 56 (2): 137–147. doi:10.1103/RevModPhys.56.137. Bibcode: 1984RvMP...56..137C.
- ↑ Bedford, D.; Krumm, P. (2004). "Heisenberg indeterminacy and the fine structure constant". American Journal of Physics 72 (7): 969. doi:10.1119/1.1646135. Bibcode: 2004AmJPh..72..969B.
- ↑ Poelz, G. (5 October 2016). "An Electron Model with Synchrotron Radiation". arXiv:1206.0620v24 [physics.class-ph].
- ↑ Fritzsch, Harald (2002). "Fundamental constants at high energy". Fortschritte der Physik 50 (5–7): 518–524. doi:10.1002/1521-3978(200205)50:5/7<518::AID-PROP518>3.0.CO;2-F. Bibcode: 2002ForPh..50..518F.
- ↑ "Method of making the wave-length of sodium light the actual and practical standard of length". The Philosophical Magazine. 5th series 24 (151): 463–466. 1887. https://babel.hathitrust.org/cgi/pt?id=mdp.39015024088174&view=1up&seq=493.
- ↑ "Method of making the wave-length of sodium light the actual and practical standard of length". The American Journal of Science. 3rd series 34 (204): 427–430. 1887. https://babel.hathitrust.org/cgi/pt?id=coo.31924084352636&view=1up&seq=461. — Article reprinted same year in the Philosophical Magazine.[23]
- ↑ "Zur Quantentheorie der Spektrallinien". Annalen der Physik. 4th series 51 (17): 1–94. 1916. doi:10.1002/andp.19163561702. Bibcode: 1916AnP...356....1S. https://babel.hathitrust.org/cgi/pt?id=nyp.33433090771183&view=1up&seq=13.
- ↑ "Current advances: The fine-structure constant and quantum Hall effect". National Institute for Standards and Technology. http://physics.nist.gov/cuu/Constants/alpha.html.
- ↑ 27.0 27.1 Kragh, Helge (July 2003). "Magic number: A partial history of the fine-structure constant". Archive for History of Exact Sciences 57 (5): 395–431. doi:10.1007/s00407-002-0065-7.
- ↑ "The number 137.035...". https://mrob.com/pub/num/n-b137_035.html.
- ↑ Aoyama, Tatsumi; Kinoshita, Toichiro; Nio, Makiko (8 February 2018). "Revised and improved value of the QED tenth-order electron anomalous magnetic moment". Physical Review D 97 (3): 036001. doi:10.1103/PhysRevD.97.036001. Bibcode: 2018PhRvD..97c6001A.
- ↑ Parker, Richard H.; Yu, Chenghui; Zhong, Weicheng; Estey, Brian; Müller, Holger (2018). "Measurement of the fine-structure constant as a test of the Standard Model". Science 360 (6385): 191–195. doi:10.1126/science.aap7706. PMID 29650669. Bibcode: 2018Sci...360..191P.
- ↑ Morel, Léo; Yao, Zhibin; Cladé, Pierre; Guellati-Khélifa, Saïda (December 2020). "Determination of the fine-structure constant with an accuracy of 81 parts per trillion". Nature 588 (7836): 61–65. doi:10.1038/s41586-020-2964-7. PMID 33268866. Bibcode: 2020Natur.588...61M. https://hal.archives-ouvertes.fr/hal-03107990/file/main.pdf.
- ↑ Relativity, Gravitation, and World Structure. Clarendon Press. 1935.
- ↑ "The cosmological constants". Nature 139 (3512): 323. 1937. doi:10.1038/139323a0. Bibcode: 1937Natur.139..323D.
- ↑ "Electricity, gravity, and cosmology". Physical Review Letters 19 (13): 759–761. 1967. doi:10.1103/PhysRevLett.19.759. Bibcode: 1967PhRvL..19..759G.
- ↑ "Variability of elementary charge and quasistellar objects". Physical Review Letters 19 (16): 913–914. 1967. doi:10.1103/PhysRevLett.19.913. Bibcode: 1967PhRvL..19..913G.
- ↑ Uzan, J.-P. (2003). "The fundamental constants and their variation: Observational status and theoretical motivations". Reviews of Modern Physics 75 (2): 403–455. doi:10.1103/RevModPhys.75.403. Bibcode: 2003RvMP...75..403U.
- ↑ Uzan, J.-P. (2004). "Variation of the constants in the late and early universe". AIP Conference Proceedings 736: 3–20. doi:10.1063/1.1835171. Bibcode: 2004AIPC..736....3U.
- ↑ Olive, K.; Qian, Y.-Z. (2003). "Were fundamental constants different in the past?". Physics Today 57 (10): 40–45. doi:10.1063/1.1825267. Bibcode: 2004PhT....57j..40O.
- ↑ Barrow, J.D. (2002). The Constants of Nature: From Alpha to Omega – the Numbers That Encode the Deepest Secrets of the Universe. Random House. ISBN 978-0-09-928647-9.
- ↑ Uzan, J.-P.; Leclercq, B. (2008). The Natural Laws of the Universe: Understanding fundamental constants. Springer-Praxis Books in Popular Astronomy. Springer Praxis. ISBN 978-0-387-73454-5. Bibcode: 2008nlu..book.....U.
- ↑ Fujii, Yasunori (2004). "Oklo constraint on the time-variability of the fine-structure constant". Astrophysics, Clocks, and Fundamental Constants. Lecture Notes in Physics. 648. pp. 167–185. doi:10.1007/978-3-540-40991-5_11. ISBN 978-3-540-21967-5.
- ↑ Webb, John K.; Flambaum, Victor V.; Churchill, Christopher W.; Drinkwater, Michael J.; Barrow, John D. (February 1999). "Search for time variation of the fine structure constant". Physical Review Letters 82 (5): 884–887. doi:10.1103/PhysRevLett.82.884. Bibcode: 1999PhRvL..82..884W.
- ↑ Murphy, M.T.; Webb, J.K.; Flambaum, V.V.; Dzuba, V.A.; Churchill, C.W.; Prochaska, J.X. et al. (11 November 2001). "Possible evidence for a variable fine-structure constant from QSO absorption lines: motivations, analysis and results". Monthly Notices of the Royal Astronomical Society 327 (4): 1208–1222. doi:10.1046/j.1365-8711.2001.04840.x. Bibcode: 2001MNRAS.327.1208M.
- ↑ Webb, J.K.; Murphy, M.T.; Flambaum, V.V.; Dzuba, V.A.; Barrow, J.D.; Churchill, C.W. et al. (9 August 2001). "Further evidence for cosmological evolution of the fine structure constant". Physical Review Letters 87 (9): 091301. doi:10.1103/PhysRevLett.87.091301. PMID 11531558. Bibcode: 2001PhRvL..87i1301W.
- ↑ Murphy, M.T.; Webb, J.K.; Flambaum, V.V. (October 2003). "Further evidence for a variable fine-structure constant from Keck/HIRES QSO absorption spectra". Monthly Notices of the Royal Astronomical Society 345 (2): 609–638. doi:10.1046/j.1365-8711.2003.06970.x. Bibcode: 2003MNRAS.345..609M.
- ↑ Chand, H.; Srianand, R.; Petitjean, P.; Aracil, B. (April 2004). "Probing the cosmological variation of the fine-structure constant: Results based on VLT-UVES sample". Astronomy & Astrophysics 417 (3): 853–871. doi:10.1051/0004-6361:20035701. Bibcode: 2004A&A...417..853C.
- ↑ Srianand, R.; Chand, H.; Petitjean, P.; Aracil, B. (26 March 2004). "Limits on the time variation of the electromagnetic fine-structure constant in the low energy limit from absorption lines in the spectra of distant quasars". Physical Review Letters 92 (12): 121302. doi:10.1103/PhysRevLett.92.121302. PMID 15089663. Bibcode: 2004PhRvL..92l1302S.
- ↑ Murphy, M.T.; Webb, J.K.; Flambaum, V.V. (6 December 2007). "Comment on "Limits on the time Variation of the electromagnetic fine-structure constant in the low energy limit from absorption lines in the spectra of distant quasars"". Physical Review Letters 99 (23): 239001. doi:10.1103/PhysRevLett.99.239001. PMID 18233422. Bibcode: 2007PhRvL..99w9001M.
- ↑ Murphy, M.T.; Webb, J.K.; Flambaum, V.V. (March 2008). "Revision of VLT/UVES constraints on a varying fine-structure constant". Monthly Notices of the Royal Astronomical Society 384 (3): 1053–1062. doi:10.1111/j.1365-2966.2007.12695.x. Bibcode: 2008MNRAS.384.1053M.
- ↑ King, J.A.; Mortlock, D.J.; Webb, J.K.; Murphy, M.T. (2009). "Markov chain Monte Carlo methods applied to measuring the fine structure constant from quasar spectroscopy". Memorie della Societa Astronomica Italiana 80: 864. Bibcode: 2009MmSAI..80..864K.
- ↑ Kurzweil, R. (2005). The Singularity is Near. Viking Penguin. pp. 139–140. ISBN 978-0-670-03384-3.
- ↑ Lamoreaux, S.K.; Torgerson, J.R. (2004). "Neutron moderation in the Oklo natural reactor and the time variation of alpha". Physical Review D 69 (12): 121701. doi:10.1103/PhysRevD.69.121701. Bibcode: 2004PhRvD..69l1701L.
- ↑ Reich, E.S. (30 June 2004). "Speed of light may have changed recently". New Scientist. https://www.newscientist.com/article/dn6092-speed-of-light-may-have-changed-recently.html. Retrieved 30 January 2009.
- ↑ "Scientists discover one of the constants of the universe might not be constant". 12 May 2005. https://www.sciencedaily.com/releases/2005/05/050512120842.htm.
- ↑ 55.0 55.1 Khatri, Rishi; Wandelt, Benjamin D. (14 March 2007). "21 cm radiation: A new probe of variation in the fine-structure constant". Physical Review Letters 98 (11): 111301. doi:10.1103/PhysRevLett.98.111301. PMID 17501040. Bibcode: 2007PhRvL..98k1301K.
- ↑ Rosenband, T.; Hume, D.B.; Schmidt, P.O.; Chou, C.W.; Brusch, A.; Lorini, L. et al. (28 March 2008). "Frequency ratio of Al+ and Hg+ single-ion optical clocks; metrology at the 17th decimal place". Science 319 (5871): 1808–1812. doi:10.1126/science.1154622. PMID 18323415. Bibcode: 2008Sci...319.1808R. https://zenodo.org/record/1230892.
- ↑ Barrow, John D.; Sandvik, Håvard Bunes; Magueijo, João (21 February 2002). "Behavior of varying-alpha cosmologies". Physical Review D 65 (6): 063504. doi:10.1103/PhysRevD.65.063504. Bibcode: 2002PhRvD..65f3504B.
- ↑ Johnston, H. (2 September 2010). "Changes spotted in fundamental constant". https://physicsworld.com/a/changes-spotted-in-fundamental-constant/.
- ↑ Webb, J.K.; King, J.A.; Murphy, M.T.; Flambaum, V.V.; Carswell, R.F.; Bainbridge, M.B. (31 October 2011). "Indications of a spatial variation of the fine structure constant". Physical Review Letters 107 (19): 191101. doi:10.1103/PhysRevLett.107.191101. PMID 22181590. Bibcode: 2011PhRvL.107s1101W.
- ↑ King, Julian A. (1 February 2012). Searching for variations in the fine-structure constant and the proton-to-electron mass ratio using quasar absorption lines (Thesis). arXiv:1202.6365. Bibcode:2012PhDT........14K. CiteSeerX 10.1.1.750.8595. hdl:1959.4/50886.
- ↑ 61.0 61.1 Zyga, Lisa (21 October 2010). "Taking a second look at evidence for the 'varying' fine-structure constant". https://phys.org/news/2010-10-evidence-varying-fine-structure-constant.html.
- ↑ "Poles and directions". Australian Government. https://www.antarctica.gov.au/about-antarctica/geography-and-geology/geography/poles-and-directions/.
- ↑ Wilczynska, Michael R.; Webb, John K.; Bainbridge, Matthew; Barrow, John D.; Bosman, Sarah E.I.; Carswell, Robert F. et al. (1 April 2020). "Four direct measurements of the fine-structure constant 13 billion years ago". Science Advances 6 (17): eaay9672. doi:10.1126/sciadv.aay9672. PMID 32917582. Bibcode: 2020SciA....6.9672W.
- ↑ "Why I'm Skeptical about the changing fine-structure constant". 14 October 2010. http://scienceblogs.com/principles/2010/09/14/httpksjtrackermitedu20100907e/.
- ↑ "The fine structure constant is probably constant". 18 October 2010. http://www.preposterousuniverse.com/blog/2010/10/18/the-fine-structure-constant-is-probably-constant/.
- ↑ Milaković, Dinko; Lee, Chung-Chi; Carswell, Robert F.; Webb, John K.; Molaro, Paolo; Pasquini, Luca (5 March 2021). "A new era of fine structure constant measurements at high redshift". Monthly Notices of the Royal Astronomical Society 500: 1–21. doi:10.1093/mnras/staa3217.
- ↑ da Fonseca, Vitor; Barreiro, Tiago; Nunes, Nelson J.; Cristiani, Stefano; Cupani, Guido; D'Odorico, Valentina et al. (2022). "Fundamental physics with ESPRESSO: Constraining a simple parametrisation for varying α". Astronomy & Astrophysics 666: A57. doi:10.1051/0004-6361/202243795. Bibcode: 2022A&A...666A..57D.
- ↑ Barrow, John D. (2001). "Cosmology, life, and the anthropic principle". Annals of the New York Academy of Sciences 950 (1): 139–153. doi:10.1111/j.1749-6632.2001.tb02133.x. PMID 11797744. Bibcode: 2001NYASA.950..139B.
- ↑ Newman, J.R., ed (1956). "The constants of nature". The World of Mathematics. 2. Simon & Schuster. pp. 1074–1093.
- ↑ Whittaker, Edmund (1945). "Eddington's theory of the constants of nature". The Mathematical Gazette 29 (286): 137–144. doi:10.2307/3609461.
- ↑ Falk, Dan (24 April 2009). "Cosmic numbers: Pauli and Jung's love of numerology". New Scientist (2705). https://www.newscientist.com/article/mg20227051.800-cosmic-numbers-pauli-and-jungs-love-of-numerology.html.
- ↑ Várlaki, Péter; Nádai, László; Bokor, József (2008). "Number archetypes and 'background' control theory concerning the fine structure constant". Acta Polytechica Hungarica 5 (2): 71–104. http://eprints.sztaki.hu/id/eprint/4822.
- ↑ 73.0 73.1 Miller, A.I. (2009). Deciphering the Cosmic Number: The Strange Friendship of Wolfgang Pauli and Carl Jung. W.W. Norton & Co. p. 253. ISBN 978-0-393-06532-9. https://archive.org/details/isbn_9780393065329/page/253.
- ↑ "A quantal hypothesis for hadrons and the judging of physical numerology". Disorder in Physical Systems. Oxford University Press. 1990. p. 141. ISBN 978-0-19-853215-6. https://www.statslab.cam.ac.uk/~grg/books/hammfest/9-jg.ps.
- ↑ A Brief History of Time. Bantam Books. 1988. pp. 7, 125. ISBN 978-0-553-05340-1. https://archive.org/details/briefhistoryofti00step_1.
- ↑ The asymptotic value of α for larger observation distances, is intended here. Caption: Fig 1.5. Screening of the (a) electric charge and (b) the color charge in quantum field theory. Graph of Electron charge versus Distance from the bare e- charge. From: Halzen, F.; Martin, A.D. (1984). Quarks and Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 978-0-471-88741-6, p. 13.
- ↑ Halzen, F.; Martin, A.D. (1984). Quarks and Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. p. 13. ISBN 978-0-471-88741-6. https://archive.org/details/quarksleptonsint0000halz.
- ↑ MacGregor, M.H. (2007). The Power of Alpha. World Scientific. p. 69. ISBN 978-981-256-961-5.
External links
- "Theories of the fine structure constant α". Atomic Physics. 3. 1973. pp. 73–84. doi:10.1007/978-1-4684-2961-9_4. ISBN 978-1-4684-2963-3. http://lss.fnal.gov/archive/1972/pub/Pub-72-059-T.pdf.
- "The fine structure constant". National Institute of Standards and Technology. http://physics.nist.gov/cuu/Constants/alpha.html. (adapted from the Encyclopædia Britannica, 15th ed. by NIST)
- "CODATA recommended value of α". 2010. http://physics.nist.gov/cuu/Constants/codata.pdf.
- Physicists Nail Down the ‘Magic Number’ That Shapes the Universe (Natalie Wolchover, Quanta magazine, December 2, 2020). The value of this constant is given here as 1/137.035999206 (note the difference in the last three digits). It was determined by a team of four physicists led by Saïda Guellati-Khélifa at the Kastler Brossel Laboratory in Paris.
- "Quotes about the fine structure constant". https://www.goodreads.com/quotes/tag/fine-structure-constant.
- "Fine structure constant". http://scienceworld.wolfram.com/physics/FineStructureConstant.html.
- "Inconstant constants". Scientific American. June 2005. http://www.sciam.com/article.cfm?articleID=0005BFE6-2965-128A-A96583414B7F0000&ref=sciam.
- "The fine structure constant". Brady Haran for the University of Nottingham. 2009. http://www.sixtysymbols.com/videos/finestructure.htm.
 |
