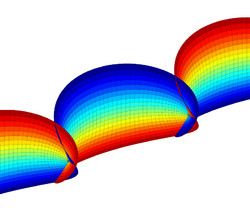
Björling problem
In differential geometry, the Björling problem is the problem of finding a minimal surface passing through a given curve with prescribed normal (or tangent planes). The problem was posed and solved by Swedish mathematician Emanuel Gabriel Björling,[1] with further refinement by Hermann Schwarz.[2]
The problem can be solved by extending the surface from the curve using complex analytic continuation. If [math]\displaystyle{ c(s) }[/math] is a real analytic curve in [math]\displaystyle{ \mathbb{R}^3 }[/math] defined over an interval I, with [math]\displaystyle{ c'(s)\neq 0 }[/math] and a vector field [math]\displaystyle{ n(s) }[/math] along c such that [math]\displaystyle{ ||n(t)||=1 }[/math] and [math]\displaystyle{ c'(t)\cdot n(t)=0 }[/math], then the following surface is minimal:
- [math]\displaystyle{ X(u,v) = \Re \left ( c(w) - i \int_{w_0}^w n(w)\times c'(w) \, dw \right) }[/math]
where [math]\displaystyle{ w = u+iv \in \Omega }[/math], [math]\displaystyle{ u_0\in I }[/math], and [math]\displaystyle{ I \subset \Omega }[/math] is a simply connected domain where the interval is included and the power series expansions of [math]\displaystyle{ c(s) }[/math] and [math]\displaystyle{ n(s) }[/math] are convergent.[3]
A classic example is Catalan's minimal surface, which passes through a cycloid curve. Applying the method to a semicubical parabola produces the Henneberg surface, and to a circle (with a suitably twisted normal field) a minimal Möbius strip.[4]
A unique solution always exists. It can be viewed as a Cauchy problem for minimal surfaces, allowing one to find a surface if a geodesic, asymptote or lines of curvature is known. In particular, if the curve is planar and geodesic, then the plane of the curve will be a symmetry plane of the surface.[5]
References
- ↑ E.G. Björling, Arch. Grunert, IV (1844) pp. 290
- ↑ H.A. Schwarz, J. reine angew. Math. 80 280-300 1875
- ↑ Kai-Wing Fung, Minimal Surfaces as Isotropic Curves in C3: Associated minimal surfaces and the Björling's problem. MIT BA Thesis. 2004 http://ocw.mit.edu/courses/mathematics/18-994-seminar-in-geometry-fall-2004/projects/main1.pdf
- ↑ W.H. Meeks III (1981). "The classification of complete minimal surfaces in R3 with total curvature greater than [math]\displaystyle{ -8\pi }[/math]". Duke Math. J. 48 (3): 523–535. doi:10.1215/S0012-7094-81-04829-8.
- ↑ Björling problem. Encyclopedia of Mathematics. URL: http://www.encyclopediaofmath.org/index.php?title=Bj%C3%B6rling_problem&oldid=23196
External image galleries
- Björling Surfaces, at the Indiana Minimal Surface Archive: http://www.indiana.edu/~minimal/archive/Bjoerling/index.html
 |