Physics:Depletion region
In semiconductor physics, the depletion region, also called depletion layer, depletion zone, junction region, space charge region, or space charge layer, is an insulating region within a conductive, doped semiconductor material where the mobile charge carriers have diffused away, or forced away by an electric field. The only elements left in the depletion region are ionized donor or acceptor impurities. This region of uncovered positive and negative ions is called the depletion region due to the depletion of carriers in this region, leaving none to carry a current. Understanding the depletion region is key to explaining modern semiconductor electronics: diodes, bipolar junction transistors, field-effect transistors, and variable capacitance diodes all rely on depletion region phenomena.
Formation in a p–n junction
A depletion region forms instantaneously across a p–n junction. It is most easily described when the junction is in thermal equilibrium or in a steady state: in both of these cases the properties of the system do not vary in time; they are in dynamic equilibrium.[1][2]
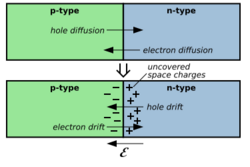
Electrons and holes diffuse into regions with lower concentrations of them, much as ink diffuses into water until it is uniformly distributed. By definition, the N-type semiconductor has an excess of free electrons (in the conduction band) compared to the P-type semiconductor, and the P-type has an excess of holes (in the valence band) compared to the N-type. Therefore, when N-doped and P-doped semiconductors are placed together to form a junction, free electrons in the N-side conduction band migrate (diffuse) into the P-side conduction band, and holes in the P-side valence band migrate into the N-side valence band.
Following transfer, the diffused electrons come into contact with holes and are eliminated by recombination in the P-side. Likewise, the diffused holes are recombined with free electrons so eliminated in the N-side. The net result is that the diffused electrons and holes are gone. In a N-side region near to the junction interface, free electrons in the conduction band are gone due to (1) the diffusion of electrons to the P-side and (2) recombination of electrons to holes that are diffused from the P-side. Holes in a P-side region near to the interface are also gone by a similar reason. As a result, majority charge carriers (free electrons for the N-type semiconductor, and holes for the P-type semiconductor) are depleted in the region around the junction interface, so this region is called the depletion region or depletion zone. Due to the majority charge carrier diffusion described above, the depletion region is charged; the N-side of it is positively charged and the P-side of it is negatively charged. This creates an electric field that provides a force opposing the charge diffusion. When the electric field is sufficiently strong to cease further diffusion of holes and electrons, the depletion region reaches the equilibrium. Integrating the electric field across the depletion region determines what is called the built-in voltage (also called the junction voltage or barrier voltage or contact potential).
Physically speaking, charge transfer in semiconductor devices is from (1) the charge carrier drift by the electric field and (2) the charge carrier diffusion due to the spatially varying carrier concentration. In the P-side of the depletion region, where holes drift by the electric field with the electrical conductivity σ and diffuse with the diffusion constant D, the net current density is given by
[math]\displaystyle{ {\bf{J}}=\sigma {\bf{E}}-e D \nabla p }[/math],
where [math]\displaystyle{ {\bf{E}} }[/math] is the electric field, e is the elementary charge (1.6×10−19 coulomb), and p is the hole density (number per unit volume). The electric field makes holes drift along the field direction, and for diffusion holes move in the direction of decreasing concentration, so for holes a negative current results for a positive density gradient. (If the carriers are electrons, the hole density p is replaced by the electron density n with negative sign; in some cases, both electrons and holes must be included.) When the two current components balance, as in the p–n junction depletion region at dynamic equilibrium, the current is zero due to the Einstein relation, which relates D to σ.
Forward bias
Forward bias (applying a positive voltage to the P-side with respect to the N-side) narrows the depletion region and lowers the barrier to carrier injection (shown in the figure to the right). In more detail, majority carriers get some energy from the bias field, enabling them to go into the region and neutralize opposite charges. The more bias the more neutralization (or screening of ions in the region) occurs. The carriers can be recombined to the ions but thermal energy immediately makes recombined carriers transition back as Fermi energy is in proximity. When bias is strong enough that the depletion region becomes very thin, the diffusion component of the current (through the junction interface) greatly increases and the drift component decreases. In this case, the net current flows from the P-side to the N-side. The carrier density is large (it varies exponentially with the applied bias voltage), making the junction conductive and allowing a large forward current.[3] The mathematical description of the current is provided by the Shockley diode equation. The low current conducted under reverse bias and the large current under forward bias is an example of rectification.
Reverse bias
Under reverse bias (applying a negative voltage to the P-side with respect to the N-side), the potential drop (i.e., voltage) across the depletion region increases. Essentially, majority carriers are pushed away from the junction, leaving behind more charged ions. Thus the depletion region is widened and its field becomes stronger, which increases the drift component of current (through the junction interface) and decreases the diffusion component. In this case, the net current flows from the N-side to the P-side. The carrier density (mostly, minority carriers) is small and only a very small reverse saturation current flows.
Determining the depletion layer width
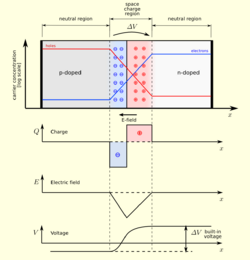
From a full depletion analysis as shown in figure 2, the charge would be approximated with a sudden drop at its limit points which in reality is gradual and is explained by Poisson's equation. The amount of flux density would then be[4]
[math]\displaystyle{ \begin{align} \frac{Q_n}{x_n} &=qN_d \\ \frac{Q_p}{x_p} &=-qN_a \\ \end{align} }[/math]
where [math]\displaystyle{ Q_n }[/math] and [math]\displaystyle{ Q_p }[/math] are the amount of negative and positive charge respectively, [math]\displaystyle{ x_n }[/math] and [math]\displaystyle{ x_p }[/math] are the distance for negative and positive charge respectively with zero at the center, [math]\displaystyle{ N_a }[/math] and [math]\displaystyle{ N_d }[/math] are the amount of acceptor and donor atoms respectively and [math]\displaystyle{ q }[/math] is the electron charge.
Taking the integral of the flux density [math]\displaystyle{ D }[/math] with respect to distance [math]\displaystyle{ dx }[/math] to determine electric field [math]\displaystyle{ E }[/math] (i.e. Gauss's law) creates the second graph as shown in figure 2:
[math]\displaystyle{ E=\frac{\int D\,dx}{\epsilon_s} }[/math]
where [math]\displaystyle{ \epsilon_s }[/math]is the permittivity of the substance. Integrating electric field with respect to distance determines the electric potential [math]\displaystyle{ V }[/math]. This would also equal to the built in voltage [math]\displaystyle{ \Delta V }[/math]as shown in Figure 2.
[math]\displaystyle{ V=\int E dx=\Delta V }[/math]
The final equation would then be arranged so that the function of depletion layer width [math]\displaystyle{ x_n }[/math]would be dependent on the electric potential [math]\displaystyle{ V }[/math].
[math]\displaystyle{ \begin{align} x_n &= \sqrt{\frac{2\epsilon_s}{q} \frac {N_a}{N_d}\frac{1}{N_a+N_d}(\Delta V)} \\ x_p &= \sqrt{\frac{2\epsilon_s}{q} \frac {N_d}{N_a}\frac{1}{N_a+N_d}(\Delta V)} \\ \end{align} }[/math]
In summary, [math]\displaystyle{ x_n }[/math] and [math]\displaystyle{ x_p }[/math] are the negative and positive depletion layer width respectively with respect to the center, [math]\displaystyle{ N_a }[/math] and [math]\displaystyle{ N_d }[/math] are the concentration of acceptor and donor atoms respectively, [math]\displaystyle{ q }[/math] is the electron charge and [math]\displaystyle{ \Delta V }[/math] is the built-in voltage, which is usually the independent variable.[4]
Formation in an MOS capacitor
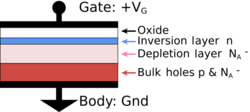
Another example of a depletion region occurs in the MOS capacitor. It is shown in the figure to the right, for a P-type substrate. Supposing that the semiconductor initially is charge neutral, with the charge due to holes exactly balanced by the negative charge due to acceptor doping impurities. If a positive voltage now is applied to the gate, which is done by introducing positive charge Q to the gate, then some positively charged holes in the semiconductor nearest the gate are repelled by the positive charge on the gate, and exit the device through the bottom contact. They leave behind a depleted region that is insulating because no mobile holes remain; only the immobile, negatively charged acceptor impurities. The greater the positive charge placed on the gate, the more positive the applied gate voltage, and the more holes that leave the semiconductor surface, enlarging the depletion region. (In this device there is a limit to how wide the depletion width may become. It is set by the onset of an inversion layer of carriers in a thin layer, or channel, near the surface. The above discussion applies for positive voltages low enough that an inversion layer does not form.)
If the gate material is polysilicon of opposite type to the bulk semiconductor, then a spontaneous depletion region forms if the gate is electrically shorted to the substrate, in much the same manner as described for the p–n junction above. For more on this, see polysilicon depletion effect.
The principle of charge neutrality says the sum of positive charges must equal the sum of negative charges:
- [math]\displaystyle{ n + N_A=p + N_D\,, }[/math]
where n and p are the number of free electrons and holes, and [math]\displaystyle{ N_D }[/math] and [math]\displaystyle{ N_A }[/math] are the number of ionized donors and acceptors "per unit of length", respectively. In this way, both [math]\displaystyle{ N_D }[/math] and [math]\displaystyle{ N_A }[/math] can be viewed as doping spatial densities. If we assume full ionization and that [math]\displaystyle{ n, p \ll N_D, N_A }[/math], then:
- [math]\displaystyle{ qN_Aw_P \approx qN_Dw_N \, }[/math].
where [math]\displaystyle{ w_P }[/math] and [math]\displaystyle{ w_N }[/math] are depletion widths in the p and n semiconductor, respectively. This condition ensures that the net negative acceptor charge exactly balances the net positive donor charge. The total depletion width in this case is the sum [math]\displaystyle{ w =w_N +w_P }[/math]. A full derivation for the depletion width is presented in reference.[5] This derivation is based on solving the Poisson equation in one dimension – the dimension normal to the metallurgical junction. The electric field is zero outside of the depletion width (seen in above figure) and therefore Gauss's law implies that the charge density in each region balance – as shown by the first equation in this sub-section. Treating each region separately and substituting the charge density for each region into the Poisson equation eventually leads to a result for the depletion width. This result for the depletion width is:
[math]\displaystyle{ w \approx \left[ \frac{2\epsilon_r\epsilon_0}{q} \left(\frac{N_A + N_D}{N_A N_D}\right) \left(V_{bi} - V\right)\right]^\frac{1}{2} }[/math]
where [math]\displaystyle{ \epsilon_r }[/math] is the relative dielectric permittivity of the semiconductor, [math]\displaystyle{ V_{bi} }[/math] is the built-in voltage, and [math]\displaystyle{ V }[/math] is the applied bias. The depletion region is not symmetrically split between the n and p regions - it will tend towards the lightly doped side.[6] A more complete analysis would take into account that there are still some carriers near the edges of the depletion region.[7] This leads to an additional -2kT/q term in the last set of parentheses above.
Depletion width in MOS capacitor
As in p–n junctions, the governing principle here is charge neutrality. Let us assume a P-type substrate. If positive charge Q is placed on gate with area A, then holes are depleted to a depth w exposing sufficient negative acceptors to exactly balance the gate charge. Supposing the dopant density to be [math]\displaystyle{ N_A }[/math] acceptors per unit volume, then charge neutrality requires the depletion width w to satisfy the relationship:
- [math]\displaystyle{ Q/A=qN_Aw \, }[/math]
If the depletion width becomes wide enough, then electrons appear in a very thin layer at the semiconductor-oxide interface, called an inversion layer because they are oppositely charged to the holes that prevail in a P-type material. When an inversion layer forms, the depletion width ceases to expand with increase in gate charge Q. In this case, neutrality is achieved by attracting more electrons into the inversion layer. In the MOSFET, this inversion layer is referred to as the channel.
Electric field in depletion layer and band bending
Associated with the depletion layer is an effect known as band bending. This effect occurs because the electric field in the depletion layer varies linearly in space from its (maximum) value [math]\displaystyle{ E_m }[/math] at the gate to zero at the edge of the depletion width:[8]
- [math]\displaystyle{ E_m={Q\over A\epsilon_0}=qN_A{w\over \epsilon_0}, \, }[/math]
where [math]\displaystyle{ \epsilon 0 }[/math] = 8.854×10−12 F/m, F is the farad and m is the meter. This linearly-varying electric field leads to an electrical potential that varies quadratically in space. The energy levels, or energy bands, bend in response to this potential.
See also
- Capacitance voltage profiling
- Metal–oxide–semiconductor structure
- Semiconductor diodes
References
- ↑ Robert H. Bishop (2002). The Mechatronics Handbook. CRC Press. ISBN 0-8493-0066-5. https://books.google.com/books?id=Q8zNV6AIvQ8C&dq=depletion-region+called+because+mobile+charge&pg=PT512.
- ↑ John E. Ayers (2003). Digital Integrated Circuits: Analysis and Design. CRC Press. ISBN 0-8493-1951-X. https://books.google.com/books?id=QHtalNXHKbsC&dq=thermal-equilibrium+depletion-region&pg=PA61.
- ↑ Sung-Mo Kang and Yusuf Leblebici (2002). CMOS Digital Integrated Circuits Analysis & Design. McGraw–Hill Professional. ISBN 0-07-246053-9. https://books.google.com/books?id=l1XyQ7RJ36cC&dq=mos-structure+depletion-region&pg=PA90.
- ↑ 4.0 4.1 "Electrostatic analysis of a p-n diode". https://ecee.colorado.edu/~bart/book/book/chapter4/ch4_3.htm.
- ↑ Pierret, Robert F. (1996). Semiconductor Device Fundamentals. pp. 209 to 216. ISBN 0201543931.
- ↑ Sasikala, B; Afzal Khan; S. Pooranchandra; B. Sasikala (2005). Introduction to Electrical , Electronics and Communication Engineering. Firewall Media. ISBN 978-81-7008-639-0.
- ↑ Kittel, C; Kroemer, H. (1980). Thermal Physics. W. H. Freeman. ISBN 0-7167-1088-9.
- ↑ Wayne M. Saslow (2002). Electricity, Magnetism, and Light. Elsevier. ISBN 0-12-619455-6.
 |