Physics:Band bending

Short description: Band bending in energy diagrams

In solid-state physics, band bending refers to the process in which the electronic band structure in a material curves up or down near a junction or interface. It does not involve any physical (spatial) bending. When the electrochemical potential of the free charge carriers around an interface of a semiconductor is dissimilar, charge carriers are transferred between the two materials until an equilibrium state is reached whereby the potential difference vanishes. The band bending concept was first developed in 1938 when Mott, Davidov and Schottky all published theories of the rectifying effect of metal-semiconductor contacts. The use of semiconductor junctions sparked the computer revolution in 1990. Devices such as the diode, the transistor, the photocell and many more still play an important role in technology.

Qualitative description

Band bending can be induced by several types of contact. In this section metal-semiconductor contact, surface state, applied bias and adsorption induced band bending are discussed.

Figure 1: Energy band diagrams of the surface contact between metals and n-type semiconductors. [math]\displaystyle{ E_{vac} }[/math], the vacuum energy; [math]\displaystyle{ E_{v} }[/math], the maximum energy of the valence band; [math]\displaystyle{ E_c }[/math], minimum energy of the conduction band; [math]\displaystyle{ \phi_m }[/math], the metal work function; [math]\displaystyle{ \phi_s }[/math], the semiconductor work function; [math]\displaystyle{ \chi_s }[/math], the electron affinity of the semiconductor.

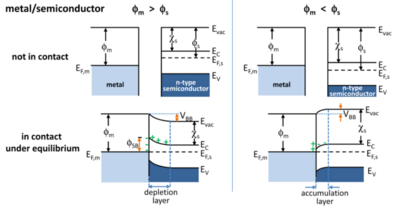
Metal-semiconductor contact induced band bending

Figure 1 shows the ideal band diagram (i.e. the band diagram at zero temperature without any impurities, defects or contaminants) of a metal with an n-type semiconductor before (top) and after contact (bottom). The work function is defined as the energy difference between the Fermi level of the material and the vacuum level before contact and is denoted by [math]\displaystyle{ \phi }[/math]. When the metal and semiconductor are brought in contact, charge carriers (i.e. free electrons and holes) will transfer between the two materials as a result of the work function difference [math]\displaystyle{ V_{BB} = |\phi_m - \phi_s| }[/math].

If the metal work function ([math]\displaystyle{ \phi_m }[/math]) is larger than that of the semiconductor ([math]\displaystyle{ \phi_s }[/math]), that is [math]\displaystyle{ \phi_m \gt \phi_s }[/math], the electrons will flow from the semiconductor to the metal, thereby lowering the semiconductor Fermi level and increasing that of the metal. Under equilibrium the work function difference vanishes and the Fermi levels align across the interface. A Helmholtz double layer will be formed near the junction, in which the metal is negatively charged and the semiconductor is positively charged due to this electrostatic induction. Consequently, a net electric field [math]\displaystyle{ \vec E }[/math] is established from the semiconductor to the metal. Due to the low concentration of free charge carriers in the semiconductor, the electric field cannot be effectively screened (unlike in the metal where [math]\displaystyle{ E=0 }[/math] in the bulk). This causes the formation of a depletion region near the semiconductor surface. In this region, the energy band edges in the semiconductor bend upwards as a result of the accumulated charge and the associated electric field between the semiconductor and the metal surface.

In the case of [math]\displaystyle{ \phi_m \lt \phi_s }[/math], electrons are shared from the metal to the semiconductor, resulting in an electric field that points in the opposite direction. Hence, the band bending is downward as can be seen in the bottom right of Figure 1.

One can envision the direction of bending by considering the electrostatic energy experienced by an electron as it moves across the interface. When [math]\displaystyle{ \phi_m \gt \phi_s }[/math], the metal develops a negative charge. An electron moving from the semiconductor to the metal therefore experiences a growing repulsion as it approaches the interface. It follows that its potential energy rises and hence the band bending is upwards. In the case of [math]\displaystyle{ \phi_m \lt \phi_s }[/math], the semiconductor carries a negative charge, forming a so-called accumulation layer and leaving a positive charge on the metal surface. An electric field develops from the metal to the semiconductor which drives the electrons towards the metal. By moving closer to the metal the electron could thus lower its potential energy. The result is that the semiconductor energy band bends downwards towards the metal surface.

Surface state induced band bending

Figure 2: Energy band diagrams under influence of surface-induced band bending. CB, the conduction band; VB, the valence band; [math]\displaystyle{ E_F }[/math], the Fermi energy; [math]\displaystyle{ E_{vac} }[/math], the vacuum energy.

Despite being energetically unfavourable, surface states may exist on a clean semiconductor surface due to the termination of the materials lattice periodicity. Band bending can also be induced in the energy bands of such surface states. A schematic of an ideal band diagram near the surface of a clean semiconductor in and out of equilibrium with its surface states is shown in Figure 2 . The unpaired electrons in the dangling bonds of the surface atoms interact with each other to form an electronic state with a narrow energy band, located somewhere within the band gap of the bulk material. For simplicity, the surface state band is assumed to be half-filled with its Fermi level located at the mid-gap energy of the bulk. Furthermore, doping is taken to not be of influence to the surface states. This is a valid approximation since the dopant concentration is low.

For intrinsic semiconductors (undoped), the valence band is fully filled with electrons, whilst the conduction band is completely empty. The Fermi level is thus located in the middle of the band gap, the same as that of the surface states, and hence there is no charge transfer between the bulk and the surface. As a result no band bending occurs. If the semiconductor is doped, the Fermi level of the bulk is shifted with respect to that of the undoped semiconductor by the introduction of dopant eigenstates within the band gap. It is shifted up for n-doped semiconductors (closer to the conduction band) and down in case of p-doping (nearing the valence band). In disequilibrium, the Fermi energy is thus lower or higher than that of the surface states for p- and n-doping, respectively. Due to the energy difference, electrons will flow from the bulk to the surface or vice versa until the Fermi levels become aligned at equilibrium. The result is that, for n-doping, the energy bands bend upward, whereas they bend downwards for p-doped semiconductors. Note that the density of surface states is large ([math]\displaystyle{ \sim10^5\text{ cm}^{-2} }[/math]) in comparison with the dopant concentration in the bulk ([math]\displaystyle{ \sim10^8-10^{12}\text{ cm}^{-2} }[/math]). Therefore, the Fermi energy of the semiconductor is almost independent of the bulk dopant concentration and is instead determined by the surface states. This is called Fermi level pinning.

Adsorption induced band bending

Figure 3: Influence of the adsorption of an acceptor molecule (A) on the surface of an n-type semiconductor.

Adsorption on a semiconductor surface can also induce band bending. Figure 3 illustrates the adsorption of an acceptor molecule (A) onto a semiconductor surface. As the molecule approaches the surface, an unfilled molecular orbital of the acceptor interacts with the semiconductor and shifts downwards in energy. Due to the adsorption of the acceptor molecule its movement is restricted. It follows from the general uncertainty principle that the molecular orbital broadens its energy as can be seen in the bottom of figure 3. The lowering of the acceptor molecular orbital leads to electron flow from the semiconductor to the molecule, thereby again forming a Helmholtz layer on the semiconductor surface. An electric field is set up and upwards band bending near the semiconductor surface occurs. For a donor molecule, the electrons will transfer from the molecule to the semiconductor, resulting in downward band bending.

Applied bias induced band bending

When a voltage is applied across two surfaces of metals or semiconductors the associated electric field is able to penetrate the surface of the semiconductor. Because the semiconductor material contains little charge carriers the electric field will cause an accumulation of charges on the semiconductor surface. When [math]\displaystyle{ V\gt 0 }[/math], a forward bias, the band bends downwards. A reverse bias ([math]\displaystyle{ V\lt 0 }[/math]) would cause an accumulation of holes on the surface which would bend the band upwards. This follows again from Poisson's equation.

As an example the band bending induced by the forming of a p-n junction or a metal-semiconductor junction can be modified by applying a bias voltage [math]\displaystyle{ V_A }[/math]. This voltage adds to the built-in potential ([math]\displaystyle{ V_{BI} }[/math]) that exists in the depletion region ([math]\displaystyle{ V_{BI} - V_A }[/math]). Thus the potential difference between the bands is either increased or decreased depending on the type of bias that is applied. The conventional depletion approximation assumes a uniform ion distribution in the depletion region. It also approximates a sudden drop in charge carrier concentration in the depletion region. Therefore the electric field changes linearly and the band bending is parabolic. Thus the width of the depletion region will change due to the bias voltage. The depletion region width is given by:

[math]\displaystyle{ w = x_n+ x_p = \sqrt{\frac{2\epsilon_s (N_A+N_D )(V_{BI} - V_A - 2kT/q)}{qN_A N_D }} }[/math]

[math]\displaystyle{ x_n }[/math] and [math]\displaystyle{ x_p }[/math] are the boundaries of the depletion region. [math]\displaystyle{ \epsilon_s }[/math] is the dielectric constant of the semiconductor. [math]\displaystyle{ N_A }[/math] and [math]\displaystyle{ N_D }[/math] are the net acceptor and net donor dopant concentrations respectively and [math]\displaystyle{ q }[/math] is the charge of the electron. The [math]\displaystyle{ 2kT/q }[/math] term compensates for the existence of free charge carriers near the junction from the bulk region.

Poisson's equation

The equation which governs the curvature obtained by the band edges in the space charge region, i.e. the band bending phenomenon, is Poisson’s equation,

[math]\displaystyle{ \triangledown^2 V = -\rho/\epsilon }[/math]

where [math]\displaystyle{ V }[/math] is the electric potential, [math]\displaystyle{ \rho }[/math] is the local charge density and [math]\displaystyle{ \epsilon }[/math] is the permittivity of the material. An example of its implementation can be found on the Wikipedia article on p-n junctions.

Applications

Electronics

The p-n diode is a device that allows current to flow in only one direction as long as the applied voltage is below a certain threshold. When a forward bias is applied to the p-n junction of the diode the band gap in the depletion region is narrowed. The applied voltage introduces more charge carriers as well, which are able to diffuse across the depletion region. Under a reverse bias this is hardly possible because the band gap is widened instead of narrowed, thus no current can flow. Therefore the depletion region is necessary to allow for only one direction of current.

The metal–oxide–semiconductor field-effect transistor (MOSFET) relies on band bending. When the transistor is in its so called ‘off state’ there is no voltage applied on the gate and the first p-n junction is reversed bias. The potential barrier is too high for the electrons to pass thus no current flows. When a voltage is applied on the gate the potential gap shrinks due to the applied bias band bending that occurs. As a result current will flow. Or in other words, the transistor is in its ‘on’ state. The MOSFET is not the only type of transistor available today. Several more examples are the Metal-Semiconductor Field Effect Transistor (MESFET) and the Junction Field Effect Transistor (JFET), both of which rely on band bending as well.

Photovoltaic cells (solar cells) are essentially just p-n diodes that can generate a current when they are exposed to sunlight. Solar energy can create an electron-hole pair in the depletion region. Normally they would recombine quite quickly before traveling very far. The electric field in the depletion region separates the electrons and holes generating a current when the two sides of the p-n diode are connected. Photovoltaic cells are an important supplier of renewable energy. They are a promising source of reliable clean energy.

Spectroscopy

Different spectroscopy methods make use of or can measure band bending:

• Surface photovoltage is a spectroscopy method used to determine the minority carrier diffusion length of semiconductors. The band bending at the surface of a semiconductor results in a depletion region with a surface potential. A photon source creates electron-hole pairs deeper into the material. These electrons then diffuse to the surface to radiatively recombine. This results in a changing surface potential which can be measured and is directly correlated to the minority carrier diffusion length. This property of a semiconductor is very important for certain electronics such as photodiodes, solar panels and transistors.
• Time-resolved Photoluminescence is another technique used to measure the minority carrier diffusion length in semiconductors. It is a form of photoluminescence spectroscopy where the emitted photon decay is measured over time. In photoluminescence spectroscopy a material is excited using a photon pulse with a higher photon energy than the band gap in the material. The material relaxes back into its ground state under emission of a photon. These emitted photons are measured to gain information about the band structure of a material.
• Angle-resolved photoemission spectroscopy can be used to chart the electronic energy bands of crystal structures such as semiconductors. This can thus also visualize band bending. The technique is an enhanced version of regular photoemission spectroscopy. It is based on the photoelectric effect. By analysing the energy difference between the incident photons and the electrons emitted by the solid, information about the energy band differences in the solid can be gained. By measuring at different angles the band structure can be mapped and the band bending captured.

See also

• Field effect (semiconductor) – band bending due to the presence of an external electric field at the vacuum surface of a semiconductor.
• Thomas–Fermi screening – special case of Lindhard theory that describes the band bending caused by a charged defect.
• Quantum capacitance – Field effect band bending, especially important for low-density-of-states-systems.