Physics:Maxwell construction
In thermodynamic equilibrium, a necessary condition for stability is that pressure, [math]\displaystyle{ p }[/math], does not increase with molar volume, [math]\displaystyle{ v=V/N }[/math]; this is expressed mathematically as [math]\displaystyle{ \partial_vp|_T\lt 0 }[/math], where [math]\displaystyle{ T }[/math] is the temperature.[1]
This basic stability requirement, and similar ones for other conjugate pairs of variables, is violated in analytic models of first order phase transitions. The most famous case is the van der Waals equation,[2][3] [math]\displaystyle{ p=RT/(v-b)-a/v^2 }[/math] where [math]\displaystyle{ a, b, R }[/math] are dimensional constants. This violation is not a defect, rather it is the origin of the observed discontinuity in properties that distinguish liquid from vapor, and defines a first order phase transition.
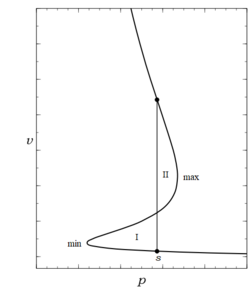
Figure 1 shows an isotherm drawn, for [math]\displaystyle{ v\gt b }[/math], as a continuously differentiable solid black, dotted black, and dashed gray curve. The decreasing right hand part of the curve in Fig. 1 describes a gas, while its left decreasing part describes a liquid. These two parts are separated by a region between the local minimum and local maximum on the curve with positive slope that violates the stability criterion. This mathematical criterion expresses a physical condition which Epstein[4] described as follows:
It is obvious that this middle part, dotted in our curves [dashed in Fig.1 here], can have no physical reality. In fact, let us imagine the fluid in a state corresponding to this part of the curve contained in a heat conducting vertical cylinder whose top is formed by a piston. The piston can slide up and down in the cylinder, and we put on it a load exactly balancing the pressure of the gas. If we take a little weight off the piston, there will no longer be equilibrium and it will begin to move upward. However, as it moves the volume of the gas increases and with it its pressure. The resultant force on the piston gets larger, retaining its upward direction. The piston will, therefore, continue to move and the gas to expand until it reaches the state represented by the maximum of the isotherm. Vice versa, if we add ever so little to the load of the balanced piston, the gas will collapse to the state corresponding to the minimum of the isotherm`
This situation is similar to a body exactly balanced at the top of a smooth surface that, with the slightest disturbance will depart from its equilibrium position and continue until it reaches a local minimum. As they are described such states are dynamically unstable, and consequently they are not observed. The gap [math]\displaystyle{ v_{\rm min}\le v\le v_{\rm max} }[/math] is a precursor of the actual phase change from liquid to vapor. The points [math]\displaystyle{ (p_{\rm min}, v_{\rm min}) }[/math] and [math]\displaystyle{ (p_{\rm max}, v_{\rm max}) }[/math], where [math]\displaystyle{ \partial_vp|_T=0 }[/math], that delimit the largest possible liquid and smallest possible vapor states are called spinodal points. Their locus forms a spinodal curve which bounds a region where no homogeneous stable states can exist.
Experiments show that if the volume of a vessel containing a fixed amount of liquid is heated and expands at constant temperature, at a certain pressure, [math]\displaystyle{ p_s(T) }[/math], vapor, (denoted by dots at points [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] in Fig. 1) bubbles nucleate so the fluid is no longer homogeneous, but rather it has become heterogeneous. It is now a mixture of two separate components, a boiling (saturated) liquid, [math]\displaystyle{ v_f=V_f/N_f }[/math], and a condensing (saturated) vapor, [math]\displaystyle{ v_g=V_g/N_g }[/math] that coexist at the same saturation temperature and pressure. As the heating continues the amount of vapor, [math]\displaystyle{ N_g }[/math] increases and that of the liquid, [math]\displaystyle{ N_f=N-N_g }[/math], decreases. All the while the pressure, [math]\displaystyle{ p_s }[/math] and temperature, [math]\displaystyle{ T }[/math], remain constant and the volume [math]\displaystyle{ V=V_f+V_g }[/math] increases. In this situation the molar volume of the mixture is a weighted average of its components [math]\displaystyle{ v=V/N=(V_f/N_f)(N-N_g)/N+(V_g/N_g)(N_g/N)=v_f(1-x)+v_gx }[/math] where [math]\displaystyle{ x=N_g/N }[/math], the mole fraction of the vapor, [math]\displaystyle{ 0\le x\le 1 }[/math], increases continuously; however, the molar volume of the substance itself has only the largest possible stable value for its liquid state, and smallest possible stable value for its vapor state at the given [math]\displaystyle{ p(T) }[/math]. To repeat, although the mixture molar volume passes continuously from [math]\displaystyle{ v_f }[/math] to [math]\displaystyle{ v_g }[/math] (denoted by the dashed line in Fig. 1), the underlying fluid has a discontinuity in this property, and others as well. This equation of state of the mixture is called the lever rule.[5][6]
The dotted parts of the curve in Fig. 1 are metastable states. For many years such states were an academic curiosity; Callen[7] gave as an example,
water that has been cooled below 0°C at a pressure of 1 atm. A tap on a beaker of water in this condition precipitates a sudden dramatic crystallization of the system.
However, studies of boiling heat transfer have made clear that metastable states occur routinely as an integral part of this process. In it the heating surface temperature is higher than the saturation temperature, often significantly so, hence the adjacent liquid must be superheated.[8] Further the advent of devices that operate with very high heat fluxes has created interest in the metastable states, and the thermodynamic properties associated with them, in particular the superheated liquid states.[9] Moreover, the fact that they are predicted by the van der Waals equation, and cubic equations in general, is compelling evidence of its efficacy in describing phase transitions; Sommerfield[10] described this as follows:
It is very remarkable that the theory due to van der Waals is in a position to predict, at least qualitatively, the existence of the unstable [called metastable here] states along the branches AA` or BB` [BC and FE in Fig. 1 here].
Equal area rule
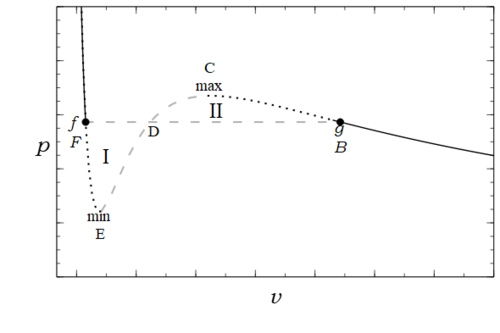
The discontinuity in [math]\displaystyle{ v }[/math], and other properties, e.g. internal energy, [math]\displaystyle{ u }[/math], and entropy,[math]\displaystyle{ s }[/math], of the substance, is called a first order phase transition.[11][12] In order to specify the unique experimentally observed pressure, [math]\displaystyle{ p_s(T) }[/math], at which it occurs another thermodynamic condition is required, for from Fig.1 it could clearly occur for any pressure in the range [math]\displaystyle{ p_{\rm min}\le p\le p_{\rm max} }[/math]. Such a condition was first enunciated in a clever thermodynamic argument by Maxwell at a lecture he delivered to the British Chemical Society on Feb 18, 1875[13] (Fig.1, including the letters B C D E F, is the curve he described):
Script error: No such module "in5".The portion of the curve from C to E represents points which are essentially unstable, and which cannot therefore be realized.
Script error: No such module "in5".Now let us suppose the medium to pass from B to F along the hypothetical curve B C D E F in a state always homogeneous, and to return along the straight line path F B in the form of a mixture of liquid and vapor. Since the temperature has been constant throughout, no heat can have been transformed into work. Now the heat transformed into work is represented by the excess of the area F D E over B C D. Hence the condition which determines the maximum pressure of the vapor at given temperature is that the line B F cuts off equal areas from the curve above and below.
The easiest way to understand Maxwell's argument is to consider the cycle he suggested on a temperature—molar entropy plane. Every introductory thermodynamics text[14] [15] presents the fact that on such a plane the area under any curve is the heat transfer to the substance per mole, positive going from left to right and negative from right to left; moreover, in a cyclic process the net heat transfer to the substance is the area enclosed by the cycle's closed curve. Since the cycle he considered is composed of the two gray dashed isothermals at the same temperature, one proceeding from B to F (through C D and E), and the other directly back from F to B, the two lines are identical, just traversed in reverse; there is zero area enclosed, and hence [math]\displaystyle{ q=0 }[/math].
Further the same texts describe the area under these curves when plotted on a pressure—molar volume, see Fig. 1, as being the work done by the substance, positive going from left to right, and negative from right to left. Likewise the net work done in a cycle is the area enclosed by the closed curve. Since the first law of thermodynamics yields in the special case of a cycle [math]\displaystyle{ w=q }[/math], for the cycle envisioned by Maxwell [math]\displaystyle{ w=q=0 }[/math]; then since the area enclosed is I+II=0, see Fig.1, with I positive and II negative, the transition pressure must be such that the two areas are equal.
Written as a mathematical equation in terms of the work done in each process this is [math]\displaystyle{ \int_{v_g}^{v_f}\,p\,dv+\int_{v_f}^{v_g}\,p_s\,dv=-\int_{v_f}^{v_g}\,p\,dv+p_s(v_g-v_f)=0\quad\mbox{for}\quad T=\mbox{constant} }[/math] This equation together with the equation of state written for each of the states [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] [math]\displaystyle{ p_s=p(v_f,T)\qquad p_s=p(v_g,T) }[/math] are three equations for the four variables, [math]\displaystyle{ p_s,T,v_f,v_g }[/math], so given any one of them, say [math]\displaystyle{ T }[/math], the other three are determined. In other words, there is a unique value of [math]\displaystyle{ p_s(T) }[/math], as well as [math]\displaystyle{ v_f(T) }[/math] and [math]\displaystyle{ v_g(T) }[/math], at which the phase transition can occur.
Gibbs criterion
At the end of his lecture, after complimenting van der Waals by referring to his work as "an exceedingly ingenious thesis", Maxwell finished it by saying:
I must not, however, omit to mention a most important American contribution to this part of thermodynamics by Prof. Willard Gibbs of Yale College U.S., who has given us a remarkably simple and thoroughly satisfactory method of representing the relations of the different states of matter by means of a model. By means of this model, problems which had long resisted the efforts of myself and others may be solved at once.
This remark proved prescient because in 1876-1878 Gibbs published his definitive work on thermodynamics [16] in which he showed that thermodynamic equilibrium of a heterogeneous substance requires that, in addition to mechanical equilibrium (the same pressure for each component) and thermal equilibrium (the same temperature for each component), there must also be material equilibrium (the same chemical potential for each component). In the present instance of one substance and two phases in addition to [math]\displaystyle{ p_f=p_g=p_s }[/math] and [math]\displaystyle{ T_f=T_g=T }[/math], material equilibrium requires [math]\displaystyle{ g_f=g_g }[/math] (for the special case of one substance its chemical potential is the molar Gibbs function, [math]\displaystyle{ \mu=g\equiv G/N }[/math] where [math]\displaystyle{ g=u+pv-Ts }[/math]). This condition can be deduced by a simple physical argument as follows: the energy required to vaporize a mole is from the second law at constant temperature [math]\displaystyle{ q_{\rm vap}=T(s_g-s_f) }[/math], and from the first law at constant pressure [math]\displaystyle{ q_{\rm vap}=h_g-h_f }[/math], then equating these two and rearranging produces the result (note that [math]\displaystyle{ h=u+pv }[/math]). The conditions of material equilibrium lead to the famous phase rule, [math]\displaystyle{ D=n-r+2 }[/math], where [math]\displaystyle{ n }[/math] is the number of substances, [math]\displaystyle{ r }[/math] the number of phases, and [math]\displaystyle{ D }[/math] the number of independent intensive variables required to specify the state.[17][18] In the case of one substance and two phases discussed here this gives, [math]\displaystyle{ D=1 }[/math], the experimentally observed number.
Now [math]\displaystyle{ g(p,T) }[/math] is a thermodynamic potential function, its differential is[19] [math]\displaystyle{ dg=\partial_pg|_T\,dp+\partial_Tg|_p\,dT=v\,dp-s\,dT }[/math]
Integrating this at constant temperature produces [math]\displaystyle{ g(p,T)=g_A(T)+\int_{p_A}^p\,v(\bar{p},T)\,d\bar{p} }[/math] here [math]\displaystyle{ g_A }[/math] is a constant of integration, but the constant is different for each isotherm hence it is written as a function of [math]\displaystyle{ T }[/math].[20] In order to evaluate [math]\displaystyle{ g }[/math] one must invert [math]\displaystyle{ p=p(v,T) }[/math] to obtain [math]\displaystyle{ v=v(p,T) }[/math]. However, it is the nature of the phase transition phenomenon that this inversion is not unique; for example the van der Waals quation written for [math]\displaystyle{ v }[/math] is, [math]\displaystyle{ pv^3-(pb+RT)v^2+av-ab=0, }[/math]
a cubic with either 1 or, in this case, 3 real roots. Thus there are three curves, as seen in Fig. 2, consisting of stable (shown solid black), metastable (shown dotted black), and unstable (shown dashed gray) states.
Actually, the figure was not produced by solving the cubic and integrating, rather [math]\displaystyle{ g(v,T) }[/math] was obtained from its definition by first obtaining [math]\displaystyle{ u(v,T) }[/math] and [math]\displaystyle{ s(v,T) }[/math], which is easily done analytically for the van der Waals equation, and plotting it parametrically with [math]\displaystyle{ p(v,T) }[/math], using [math]\displaystyle{ v }[/math] as the parameter. Note that [math]\displaystyle{ g(p,T) }[/math] is continuous with discontinuous partial derivatives, [math]\displaystyle{ \partial_pg|_T=v }[/math] and [math]\displaystyle{ \partial_Tg|_p=-s }[/math], at the phase transition point. In the Ehrenfest classification, a first order phase transition refers to the discontinuity of the first partial derivatives of [math]\displaystyle{ g }[/math] while a second order phase transition would involve discontinuities of the second partial derivatives.[21]
Relationship between the Gibbs and Maxwell criteria
Evaluating the integral expression for [math]\displaystyle{ g(p,T) }[/math] given previously between the saturated liquid and vapor states and applying the Gibbs criterion of material equilibrium to this phase change process requires writing it as [math]\displaystyle{ g_g-g_f=\int_{p_s}^{p_{\rm min}}\,v_l\,dp+ \int_{p_{\rm min}}^{p_{\rm max}}\,v_u\,dp+ \int_{p_{\rm max}}^{p_s}\,v_v\,dp=0 }[/math]
Here the integral has been split into three parts using the three real roots of the cubic corresponding to the liquid, [math]\displaystyle{ v_l }[/math], unstable, [math]\displaystyle{ v_u }[/math], and vapor, [math]\displaystyle{ v_v }[/math], states respectively. These integrals can best be visualized by viewing Fig. 1 rotated so that [math]\displaystyle{ v }[/math] is plotted on the ordinate of the curve as shown in the accompanying graph. In this view the function [math]\displaystyle{ v(p,T) }[/math] clearly is multi-valued; this is the reason it requires three real functions to describe its behavior between [math]\displaystyle{ p_{\rm min} }[/math] and [math]\displaystyle{ p_{\rm max} }[/math]. Now on splitting the middle integral into two [math]\displaystyle{ g_g-g_f=\int_{p_s}^{p_{\rm min}}\,v_l\,dp+ \int_{p_{\rm min}}^{p_s}\,v_u\,dp+\int_{p_s}^{p_{\rm max}}\,v_u\,dp+\int_{p_{\rm max}}^{p_s}\,v_v\,dp=0 }[/math] The first two integrals here are area I while the second two are the negative of area II. The two areas add to zero hence their magnitudes are equal according to this Gibbs criterion. That this must be the same as the Maxwell construction seems obvious, and it can be easily shown analytically since [math]\displaystyle{ d(pv)= pdv+vdp }[/math]. As a result, [math]\displaystyle{ dg=v\,dp-s\,dT=-p\,dv+d(pv)-s\,dT }[/math] and then integrating for constant temperature from state [math]\displaystyle{ f }[/math] to [math]\displaystyle{ g }[/math] with the Gibbs condition produces [math]\displaystyle{ g_g-g_f=-\int_{v_f}^{v_g}\,p(v,T)\,dv+p_s(v_g-v_f)=0 }[/math] which is Maxwell's result. This equal area rule can also be derived by making use of the Helmholtz free energy.[22] In any event the two conditions are the same; the Maxwell construction derives from the Gibbs condition of material equilibrium. Although [math]\displaystyle{ g_f=g_g }[/math] is more fundamental, the Maxwell construction often requires less effort to implement.
Application to the van der Waals equation
From the van der Waals equation applied to the saturated liquid, [math]\displaystyle{ v_f\lt v_{\rm min} }[/math], and vapor, [math]\displaystyle{ v_g\gt v_{\rm max} }[/math], states [math]\displaystyle{ p_s=\frac{RT_s}{v_f-b}-\frac{a}{v_f^2}\qquad p_s=\frac{RT_s}{v_g-b}-\frac{a}{v_g^2} }[/math] These two equations specify 4 variables so they can be solved for [math]\displaystyle{ p_s, T_s }[/math] in terms of [math]\displaystyle{ v_f, v_g }[/math]. This results in [math]\displaystyle{ p_s=p^*\frac{v^{*2}[v_fv_g-v^*(v_f+v_g)]}{v_f^2v_g^2}\qquad T_s=T^*\frac{v^*(v_f+v_g)(v_f-v^*)(v_g-v^*)} {v_f^2v_g^2} }[/math] where [math]\displaystyle{ p^*=a/b^2 }[/math], [math]\displaystyle{ v^*=b }[/math], and [math]\displaystyle{ T^*=a/(Rb) }[/math] are a characteristic pressure, molar volume, and temperature defined by the constants (note that [math]\displaystyle{ p^*v^*/T^*=R }[/math]). Applying the Maxwell construction to the van der Waals equation gives [math]\displaystyle{ -T_s\ln\left(\frac{v_g-v^*}{v_f-v^*}\right)+T^*\frac{v^*(v_g-v_f)}{v_fv_g}+p_s(v_g-v_f)/R=0 }[/math] These three equations can be solved numerically. This has been done given a value for either [math]\displaystyle{ T_s }[/math] or [math]\displaystyle{ p_s }[/math], and tabular results presented;[23][24] however, the equations also admit an analytic parametric solution that, according to Lenkner,[25] was obtained by Gibbs. Lenkner himself devised a simple, elegant, method to obtain this solution, by eliminating [math]\displaystyle{ p_s }[/math] and [math]\displaystyle{ T_s }[/math] from the equations, and writing them in terms of a stretched dimensionless number density, [math]\displaystyle{ \varrho=v^*/(v-v^*) }[/math], that varies between [math]\displaystyle{ \infty }[/math] and 0 as [math]\displaystyle{ v }[/math] varies from [math]\displaystyle{ v^* }[/math] to [math]\displaystyle{ \infty }[/math]; this produces [math]\displaystyle{ \ln\left(\frac{\varrho_f}{\varrho_g}\right)=\frac{(\varrho_f-\varrho_g)(\varrho_g+\varrho_f+2)}{\varrho_f+\varrho_g+2\varrho_f\varrho_g} }[/math] Although transcendental, this equation has a simple analytic, parametric solution obtained by writing the left side of the equation, which is just [math]\displaystyle{ (s_g-s_f)/R }[/math], as [math]\displaystyle{ \ln\left(\frac{\varrho_f}{\varrho_g}\right)=\frac{s_g-s_f}{R}=\delta=2y }[/math] Then [math]\displaystyle{ \varrho_f=e^{\delta}\varrho_g }[/math] and when used to eliminate [math]\displaystyle{ \varrho_f }[/math] from the right hand side a linear equation for [math]\displaystyle{ \varrho_g }[/math] is obtained, whose solution is [math]\displaystyle{ \varrho_g(y)=f(y)e^{-y}\quad\mbox{and}\quad\varrho_f(y)=f(y)e^y\quad \mbox{where}\quad f(y)=\frac{y\cosh y-\sinh y}{\sinh y\cosh y-y} }[/math] Accordingly, the fundamental variable that specifies all the others in this phase transition process is [math]\displaystyle{ (s_g-s_f)/(2R)=y }[/math]. This solution to the saturation problem is easily extended to encompass all its variables [math]\displaystyle{ T_{s}(y)=T^*\frac{2f(y)[\cosh y+f(y)]}{g(y)^2}\qquad p_{s}(y)=p^*\frac{f(y)^2[1-f(y)^2]}{g(y)^2} }[/math] [math]\displaystyle{ v_{f}(y)=v^*\frac{1+f(y)e^y}{f(y)e^y}\quad\quad\quad\quad\quad\quad v_{g}(y)=v^*\frac{1+f(y)e^{-y}}{f(y)e^{-y}} }[/math] where [math]\displaystyle{ g(y)=[1+\varrho_g(y)][1+\varrho_f(y)]=1+2f(y)\cosh y+f(y)^2 }[/math].
The values of all other property discontinuities across the saturation curve also follow from this solution.[26]
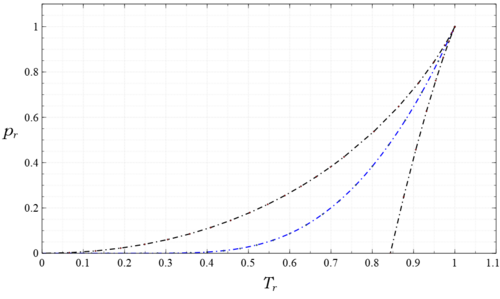
These functions define the coexistence curve which is the locus of the saturated liquid and saturated vapor states of the van der Waals fluid. In Fig. 3 this curve is plotted in blue together with the spinodal curve in black, calculated from [math]\displaystyle{ T=T^*(\tilde{v}-1)^2/\tilde{v}^3\quad\quad p=p^*(\tilde{v}-2)/\tilde{v}^3 }[/math] where [math]\displaystyle{ \tilde{v}=v/v^* }[/math] is a parameter. The variables used in making these plots are the reduced (dimensionless) variables, [math]\displaystyle{ p_r=p/p_c }[/math], [math]\displaystyle{ v_r=v/v_c }[/math], and [math]\displaystyle{ T_r=T/T_c }[/math] where the [math]\displaystyle{ c }[/math] subscripted quantities are the critical point values. They are defined by, [math]\displaystyle{ \partial_vp|_T=0 }[/math], and [math]\displaystyle{ \partial^2_vp|_T=0 }[/math] at the critical point,[27] and are measurable quantities. The relations [math]\displaystyle{ p^*/p_c=27 }[/math], [math]\displaystyle{ v^*/v_c=1/3 }[/math], [math]\displaystyle{ T^*/T_c=27/8 }[/math] are used to convert the star quantities in the solution to the [math]\displaystyle{ c }[/math] quantities used in the figures. The curve agrees completely with the numerical results referenced earlier. In the region inside the spinodal curve there are two states at each point, one stable and one metastable, either superheated liquid to the right of the blue curve, or subcooled vapor to the left, while outside the spinodal curve there is one stable state at each point. In Fig. 4 the region under the (dot dash black) spinodal curve contains no stable states while between the (dot dash red) coexistence and spinodal curves there is one metastable state at every point, and outside the coexistence curve there is one stable state at each point. The two blue and two green circles denote the saturated liquid and vapor states on their respective isotherms. There are also observed heterogeneous states everywhere under the red coexistence curve that satisfy the lever rule; however, they are not homogeneous states of the van der Waals equation, so their existence, indicated by horizontal lines connecting the saturation points on each subcritical isotherm, is not displayed. Also the abscissa in this figure is logarithmic, not linear, in order to show more of the vapor region at large [math]\displaystyle{ v_r }[/math] without excessively compressing the liquid and unstable regions at small [math]\displaystyle{ v_r }[/math]; however, this device distorts areas, so the two areas I and II in Fig.1 would not appear equal here.
Over the parameter range [math]\displaystyle{ 0\le y\lt \infty }[/math], [math]\displaystyle{ f(y) }[/math] decreases monotonically from [math]\displaystyle{ f(0)=1 }[/math] and approaches 0 as[math]\displaystyle{ f(y)\sim 2(y-1)e^{-y} }[/math] in the limit [math]\displaystyle{ y\rightarrow\infty }[/math]. Therefore [math]\displaystyle{ \varrho_f(0)=\varrho_g(0)=1/2 }[/math] and in the limit [math]\displaystyle{ y \rightarrow\infty }[/math], [math]\displaystyle{ \varrho_f(y)\sim 2(y-1) }[/math] and [math]\displaystyle{ \varrho_g(y)\sim 2(y-1)e^{-2y} }[/math]. The behavior of [math]\displaystyle{ p_s(y) }[/math] and [math]\displaystyle{ T_s(y) }[/math] follow from the equations. Both these properties also decrease monotonically from [math]\displaystyle{ p_s(0)=p^*/27 }[/math] and [math]\displaystyle{ T_s(0)=8T^*/27 }[/math], and approach 0 as [math]\displaystyle{ p_s\sim p^*\varrho_g/\varrho_f }[/math] and [math]\displaystyle{ T_s\sim T^*/\varrho_f }[/math] in the limit [math]\displaystyle{ y\rightarrow\infty }[/math]. Note from these that [math]\displaystyle{ p_s\sim (p^*/T^*)T_s\varrho_g\sim (p^*v^*/T^*)T_s\rho_g=\rho_gRT_s }[/math]; the van der Waals saturated vapor is an ideal gas in this limit. To paraphrase Sommerfield, it is remarkable that the theory due to van der Waals is able to predict that when [math]\displaystyle{ s_g-s_f\gg 2R }[/math] the saturated vapor behaves like an ideal gas; the saturated vapor of real gases behave exactly this way.
In addition for [math]\displaystyle{ T_r\lt 27/32=0.84375 }[/math] the liquid spinodal point occurs at a negative pressure, and the isotherm [math]\displaystyle{ T_r=0.8 }[/math] is included in Fig. 4 to illustrate this point. This means that some part of those liquid metastable states are in tension, and the lower the temperature the greater the tensile stress. Although this seems counterintuitive it is known that under some circumstances liquids can support tension. Tien and Lienhard[28] noted this and wrote:
The van der Waals equation predicts that at low temperatures liquids sustain enormous tension---a fact that has led some authors to take the equation lightly. In recent years measurements have been made that reveal this to be entirely correct.[29] Liquids that are clean and free of dissolved gas can be subjected to tensions greater in magnitude than [math]\displaystyle{ p_c }[/math].
This is another interesting feature of the van der Waals theory.
Common tangent construction and lever rule
The Maxwell construction is related to the common tangent construction[30][31] and the lever rule.[32]
See also
References
- ↑ Callen, H.B., Thermodynamics}, John Wiley & Sons, N.Y., pp 131-135, (1960}
- ↑ van der Waals, J.D., Ph.D. Thesis, Leiden Univ. (1873); English Translation J.S. Rowlinson, On the Continuity of the Gaseous and Liquid States, Dover, N.Y. (1988)
- ↑ Epstein, P.S., Textbook of Thermodynamics, John Wiley & Sons, N.Y., p 9, (1937)
- ↑ Epstein, p 10
- ↑ Callen, pp 146-163
- ↑ Goodstein, D.L., States of Matter, Dover, N.Y., pp 443-452, (1975)
- ↑ Callen, p 163
- ↑ Lienhard IV, J.H. and Lienhard V, J.H., A Heat Transfer Textbook Fifth edition, Dover, Mineola, NY, pp 467-469, (2019)
- ↑ Lienhard, J.H., The Properties and Behavior of Superheated Liquids, Lat. Am. J. Heat and Mass Transfer, 10, 169-187, (1986)
- ↑ Sommerfeld, A., Thermodynamics and Statistical Mechanics, Edited by Bopp, F. and Meixner, J., Translated by Kestin, J., Academic Press, N.Y., p. 66, (1956)
- ↑ Callen, p 146
- ↑ Goodstein, p 443
- ↑ Maxwell, J.C., On the Dynamical Evidence of the Molecular Constitution of Bodies, Nature, 11 (279), pp. 357-359, (1875)
- ↑ Van Wylen, G.J., and Sonntag, R.E., Fundamentals of Classical Thermodynamics Second Edition, John Wiley and Sons, N.Y., p. 211, (1973)
- ↑ Moran, M.J., and Shapiro, H.N., Fundamentals of Engineering Thermodynamics Fourth Edition, John Wiley & Sons, N.Y., p. 251, (2000)
- ↑ Gibbs, J.W., On the Equilibrium of Heterogeneous Substances, Transactions of the Connecticut Academy III, in The Collected Works of J. Willard Gibbs Volume I Thermodynamics, Yale University Press, New Haven, pp. 62-65, (1948)
- ↑ Gibbs, J.W., pp. 96-100
- ↑ Callen, pp 163-167
- ↑ Callen, pp. 98-100
- ↑ Callen, p 150
- ↑ Callen, pp. 172-173
- ↑ Sommerfeld, A., pp 67-68, (1956)
- ↑ Shamsundar, N. and Lienhard, J.H., Saturation and Metastable Properties of the van der Waals Fluid, Canad J Chem Eng, 61, 876-880, (1983)
- ↑ Barrufet, M.A., Eubank, P.T., Generalized Saturation Properties of Pure Fluids Via Cubic Equations of State, ASEE Chemical Engineering Education, 168-175, (1989)
- ↑ Lekner, J. {\it Parametric solution of the van der Waals liquid-vapor coexistence curve}, Am. J. Phys., {\bf 50}, 161, (1982)
- ↑ Johnston, D.C., Thermodynamic Properties of the van der Waals Fluid, arXiv:1402.1205v1, (2014)
- ↑ Sommerfeld, A., pp 56-57, (1956)
- ↑ Tien, C.L., and Lienhard, J.H., Statistical Thermodynamics Revised Printing, Hemisphere Publishing, NY, p.254, (1979)
- ↑ Temperley, H.N.V., The Behavior of Water under Hydrostatic Tension: III, Proc. Phys. Soc. (London), 59, p 199, (1947)
- ↑ Wales, David; Wales (2003) (in en). Energy Landscapes: Applications to Clusters, Biomolecules and Glasses. Cambridge University Press. p. 444. ISBN 9780521814157. https://books.google.com/books?id=YQrB6s3LALEC&q=common+%22tangent+line%22+maxwell+construction&pg=PA444.
- ↑ "First order phase transitions and the dynamics of spinodal decomposition". http://www.mhkoepf.de/Notes/Spinodal/spinodal.html.
- ↑ Kondepudi, Dilip; Prigogine, Ilya (2014-12-31) (in en). Modern Thermodynamics: From Heat Engines to Dissipative Structures. John Wiley & Sons. ISBN 9781118371817. https://books.google.com/books?id=TLrlBQAAQBAJ&q=lever+rule+maxwell+construction&pg=PA198.
- Maxwell, J. C. (1875). "On the Dynamical Evidence of the Molecular Constitution of Bodies.". Nature 11 (279): 357–359. doi:10.1038/011357a0. Bibcode: 1875Natur..11..357C.
- A Modern Course in Statistical Physics (3rd ed.). New York, NY USA: Wiley-VCH. 2009. ISBN 9783527407828.
 |