Lever rule
In chemistry, the lever rule is a formula used to determine the mole fraction (xi) or the mass fraction (wi) of each phase of a binary equilibrium phase diagram. It can be used to determine the fraction of liquid and solid phases for a given binary composition and temperature that is between the liquidus and solidus line.[1]
In an alloy or a mixture with two phases, α and β, which themselves contain two elements, A and B, the lever rule states that the mass fraction of the α phase is
- [math]\displaystyle{ w^\alpha = \frac{w_{\rm B}-w_{\rm B}^\beta}{w_{\rm B}^\alpha-w_{\rm B}^\beta} }[/math]
where
- [math]\displaystyle{ w_{\rm B}^\alpha }[/math] is the mass fraction of element B in the α phase
- [math]\displaystyle{ w_{\rm B}^\beta }[/math] is the mass fraction of element B in the β phase
- [math]\displaystyle{ w_{\rm B} }[/math] is the mass fraction of element B in the entire alloy or mixture
all at some fixed temperature or pressure.
Derivation
Suppose an alloy at an equilibrium temperature T consists of [math]\displaystyle{ w_{\rm B} }[/math] mass fraction of element B. Suppose also that at temperature T the alloy consists of two phases, α and β, for which the α consists of [math]\displaystyle{ w_{\rm B}^\alpha }[/math], and β consists of [math]\displaystyle{ w_{\rm B}^\beta }[/math]. Let the mass of the α phase in the alloy be [math]\displaystyle{ m^\alpha }[/math] so that the mass of the β phase is [math]\displaystyle{ m^\beta = m - m^\alpha }[/math], where [math]\displaystyle{ m }[/math] is the total mass of the alloy.
By definition, then, the mass of element B in the α phase is [math]\displaystyle{ m_{\rm B}^\alpha = w_{\rm B}^\alpha m^\alpha }[/math], while the mass of element B in the β phase is [math]\displaystyle{ m_{\rm B}^\beta = w_{\rm B}^\beta \left(m -m^\alpha\right) }[/math]. Together these two quantities sum to the total mass of element B in the alloy, which is given by [math]\displaystyle{ m_{\rm B} = w_{\rm B}m }[/math]. Therefore,
- [math]\displaystyle{ w_{\rm B}m = m_{\rm B} = m_{\rm B}^\alpha + m_{\rm B}^\beta = w_{\rm B}^\alpha m^\alpha + w_{\rm B}^\beta \left(m - m^\alpha\right) }[/math]
By rearranging, one finds that
- [math]\displaystyle{ w^\alpha \equiv \frac{m^\alpha}{m} = \frac{ w_{\rm B}-w_{\rm B}^{\beta} }{ w_{\rm B}^{\alpha}-w_{\rm B}^{\beta} } }[/math]
This final fraction is the mass fraction of the α phase in the alloy.
Calculations
Binary phase diagrams
Before any calculations can be made, a tie line is drawn on the phase diagram to determine the mass fraction of each element; on the phase diagram to the right it is line segment LS. This tie line is drawn horizontally at the composition's temperature from one phase to another (here the liquid to the solid). The mass fraction of element B at the liquidus is given by wBl (represented as wl in this diagram) and the mass fraction of element B at the solidus is given by wBs (represented as ws in this diagram). The mass fraction of solid and liquid can then be calculated using the following lever rule equations:[1]
- [math]\displaystyle{ w^{\rm s} = \frac{w_{\rm B} - w_{\rm B}^{\rm l}}{w_{\rm B}^{\rm s} - w_{\rm B}^{\rm l}} }[/math]
- [math]\displaystyle{ w^{\rm l} = \frac{w_{\rm B}^{\rm s} - w_{\rm B}}{w_{\rm B}^{\rm s} - w_{\rm B}^{\rm l}} }[/math]
where wB is the mass fraction of element B for the given composition (represented as wo in this diagram).
The numerator of each equation is the original composition that we are interested in is +/- the opposite lever arm. That is if you want the mass fraction of solid then take the difference between the liquid composition and the original composition. And then the denominator is the overall length of the arm so the difference between the solid and liquid compositions. If you're having difficulty realising why this is so, try visualising the composition when wo approaches wl. Then the liquid concentration will start increasing.
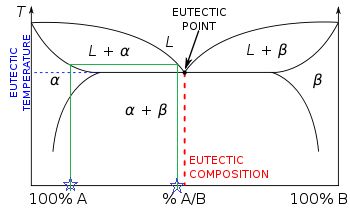
Eutectic phase diagrams
There is now more than one two-phase region. The tie line drawn is from the solid alpha to the liquid and by dropping a vertical line down at these points the mass fraction of each phase is directly read off the graph, that is the mass fraction in the x axis element. The same equations can be used to find the mass fraction of alloy in each of the phases, i.e. wl is the mass fraction of the whole sample in the liquid phase.[2]
References
- ↑ 1.0 1.1 Smith.h, William F. halkias; Hashemi, Javad (2006), Foundations of Materials Science and Engineering (4th ed.), McGraw-Hill, pp. 318–320, ISBN 0-07-295358-6.
- ↑ Callister, William D.; Rethwisch, David (2009), Materials Science and Engineering An Introduction (8th ed.), Wiley, pp. 298–303, ISBN 978-0-470-41997-7.
 |