Great triambic icosahedron
| Great triambic icosahedron | Medial triambic icosahedron | |

|

| |
| Types | Dual uniform polyhedra | |
| Symmetry group | Ih | |
| Name | Great triambic icosahedron | Medial triambic icosahedron |
| Index references | DU47, W34, 30/59 | DU41, W34, 30/59 |
| Elements | F = 20, E = 60 V = 32 (χ = -8) |
F = 20, E = 60 V = 24 (χ = -16) |
| Isohedral faces |  |

|
| Duals |  Great ditrigonal icosidodecahedron |
120px Ditrigonal dodecadodecahedron |
| Stellation | ||
| Icosahedron: W34 | ||
 Stellation diagram | ||
File:Medial triambic icosahedron.stl
In geometry, the great triambic icosahedron and medial triambic icosahedron (or midly triambic icosahedron) are visually identical dual uniform polyhedra. The exterior surface also represents the De2f2 stellation of the icosahedron. These figures can be differentiated by marking which intersections between edges are true vertices and which are not. In the above images, true vertices are marked by gold spheres, which can be seen in the concave Y-shaped areas. Alternatively, if the faces are filled with the even–odd rule, the internal structure of both shapes will differ.
The 12 vertices of the convex hull matches the vertex arrangement of an icosahedron.
Great triambic icosahedron
The great triambic icosahedron is the dual of the great ditrigonal icosidodecahedron, U47. It has 20 inverted-hexagonal (triambus) faces, shaped like a three-bladed propeller. It has 32 vertices: 12 exterior points, and 20 hidden inside. It has 60 edges.
The faces have alternating angles of [math]\displaystyle{ \arccos(\frac{1}{4})-60^{\circ}\approx 15.522\,487\,814\,07^{\circ} }[/math] and [math]\displaystyle{ \arccos(-\frac{1}{4})\approx 104.477\,512\,185\,93^{\circ} }[/math]. The sum of the six angles is [math]\displaystyle{ 360^{\circ} }[/math], and not [math]\displaystyle{ 720^{\circ} }[/math] as might be expected for a hexagon, because the polygon turns around its center twice. The dihedral angle equals [math]\displaystyle{ \arccos(-\frac{1}{3})\approx 109.471\,220\,634\,49 }[/math].
Medial triambic icosahedron
The medial triambic icosahedron is the dual of the ditrigonal dodecadodecahedron, U41. It has 20 faces, each being simple concave isotoxal hexagons or triambi. It has 24 vertices: 12 exterior points, and 12 hidden inside. It has 60 edges.
The faces have alternating angles of [math]\displaystyle{ \arccos(\frac{1}{4})-60^{\circ}\approx 15.522\,487\,814\,07^{\circ} }[/math] and [math]\displaystyle{ \arccos(-\frac{1}{4})+120^{\circ}\approx 224.477\,512\,185\,93^{\circ} }[/math]. The dihedral angle equals [math]\displaystyle{ \arccos(-\frac{1}{3})\approx 109.471\,220\,634\,49 }[/math].
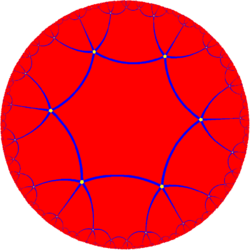
Unlike the great triambic icosahedron, the medial triambic icosahedron is topologically a regular polyhedron of index two.[1] By distorting the triambi into regular hexagons, one obtains a quotient space of the hyperbolic order-5 hexagonal tiling:
As a stellation
It is Wenninger's 34th model as his 9th stellation of the icosahedron
See also
- Triakis icosahedron
- Small triambic icosahedron
- Medial rhombic triacontahedron
References
- ↑ The Regular Polyhedra (of index two), David A. Richter
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5.
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN:0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp.96-104
External links
- Weisstein, Eric W.. "Great triambic icosahedron". http://mathworld.wolfram.com/GreatTriambicIcosahedron.html.
- Weisstein, Eric W.. "Medial triambic icosahedron". http://mathworld.wolfram.com/MedialTriambicIcosahedron.html.
- gratrix.net Uniform polyhedra and duals
- bulatov.org Medial triambic icosahedron Great triambic icosahedron
 |