Windmill graph
| Windmill graph | |
|---|---|
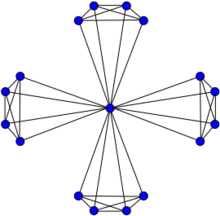 The Windmill graph Wd(5,4). | |
| Vertices | n(k – 1) + 1 |
| Edges | nk(k − 1)/2 |
| Radius | 1 |
| Diameter | 2 |
| Girth | 3 if k > 2 |
| Chromatic number | k |
| Chromatic index | n(k – 1) |
| Notation | Wd(k,n) |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the windmill graph Wd(k,n) is an undirected graph constructed for k ≥ 2 and n ≥ 2 by joining n copies of the complete graph Kk at a shared universal vertex. That is, it is a 1-clique-sum of these complete graphs.[1]
Properties
It has n(k – 1) + 1 vertices and nk(k − 1)/2 edges,[2] girth 3 (if k > 2), radius 1 and diameter 2. It has vertex connectivity 1 because its central vertex is an articulation point; however, like the complete graphs from which it is formed, it is (k – 1)-edge-connected. It is trivially perfect and a block graph.
Special cases
By construction, the windmill graph Wd(3,n) is the friendship graph Fn, the windmill graph Wd(2,n) is the star graph Sn and the windmill graph Wd(3,2) is the butterfly graph.
Labeling and colouring
The windmill graph has chromatic number k and chromatic index n(k – 1). Its chromatic polynomial can be deduced from the chromatic polynomial of the complete graph and is equal to
- [math]\displaystyle{ x\prod_{i=1}^{k-1}(x-i)^n. }[/math]
The windmill graph Wd(k,n) is proved not graceful if k > 5.[3] In 1979, Bermond has conjectured that Wd(4,n) is graceful for all n ≥ 4.[4] Through an equivalence with perfect difference families, this has been proved for n ≤ 1000. [5] Bermond, Kotzig, and Turgeon proved that Wd(k,n) is not graceful when k = 4 and n = 2 or n = 3, and when k = 5 and n = 2.[6] The windmill Wd(3,n) is graceful if and only if n ≡ 0 (mod 4) or n ≡ 1 (mod 4).[7]
Gallery
References
- ↑ Gallian, J. A. (3 January 2007). "A dynamic survey of graph labeling". Electronic Journal of Combinatorics DS6: 1–58. http://www.combinatorics.org/Surveys/ds6.pdf.
- ↑ Weisstein, Eric W.. "Windmill Graph". http://mathworld.wolfram.com/WindmillGraph.html.
- ↑ Koh, K. M.; Rogers, D. G.; Teo, H. K.; Yap, K. Y. (1980). "Graceful graphs: some further results and problems". Congressus Numerantium 29: 559–571.
- ↑ Bermond, J.-C. (1979). "Graceful graphs, radio antennae and French windmills". in Wilson, Robin J.. Graph theory and combinatorics (Proc. Conf., Open Univ., Milton Keynes, 1978). Research notes in mathematics. 34. Pitman. pp. 18–37. ISBN 978-0273084358. OCLC 757210583. https://books.google.com/books?id=7-_uAAAAMAAJ.
- ↑ Ge, G.; Miao, Y.; Sun, X. (2010). "Perfect difference families, perfect difference matrices, and related combinatorial structures". Journal of Combinatorial Designs 18 (6): 415–449. doi:10.1002/jcd.20259.
- ↑ Bermond, J.-C.; Kotzig, A.; Turgeon, J. (1978). "On a combinatorial problem of antennas in radioastronomy". in Hajnal, A.; Sos, Vera T.. Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), Vol. I. Colloquia mathematica Societatis János Bolyai. 18. North-Holland. pp. 135–149. ISBN 978-0-444-85095-9. https://books.google.com/books?id=OPtUvQEACAAJ.
- ↑ Bermond, J.-C.; Brouwer, A. E.; Germa, A. (1978). "Systèmes de triplets et différences associées". Problèmes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976). Colloques internationaux du Centre National de la Recherche Scientifique. 260. Éditions du Centre national de la recherche scientifique. pp. 35–38. ISBN 978-2-222-02070-7. https://books.google.com/books?id=0u3uAAAAMAAJ.
 |


