Graceful labeling

From HandWiki
Short description: Type of graph vertex labeling
A graceful labeling. Vertex labels are in black, edge labels in red.

In graph theory, a graceful labeling of a graph with m edges is a labeling of its vertices with some subset of the integers from 0 to m inclusive, such that no two vertices share a label, and each edge is uniquely identified by the absolute difference between its endpoints, such that this magnitude lies between 1 and m inclusive.[1] A graph which admits a graceful labeling is called a graceful graph.

The name "graceful labeling" is due to Solomon W. Golomb; this type of labeling was originally given the name β-labeling by Alexander Rosa in a 1967 paper on graph labelings.[2]

A major conjecture in graph theory is the graceful tree conjecture or Ringel–Kotzig conjecture, named after Gerhard Ringel and Anton Kotzig, and sometimes abbreviated GTC.[3] It hypothesizes that all trees are graceful. It is still an open conjecture, although a related but weaker conjecture known as "Ringel's conjecture" was partially proven in 2020.[4][5][6] Kotzig once called the effort to prove the conjecture a "disease".[7]

Another weaker version of graceful labelling is near-graceful labeling, in which the vertices can be labeled using some subset of the integers on [0, m + 1] such that no two vertices share a label, and each edge is uniquely identified by the absolute difference between its endpoints (this magnitude lies on [1, m + 1]).

Another conjecture in graph theory is Rosa's conjecture, named after Alexander Rosa, which says that all triangular cacti are graceful or nearly-graceful.[8]

A graceful graph with edges 0 to m is conjectured to have no fewer than [math]\displaystyle{ \left\lceil \sqrt{3 m+\tfrac{9}{4}} \right\rfloor }[/math] vertices, due to sparse ruler results. This conjecture has been verified for all graphs with 213 or fewer edges.

A graceful graph with 27 edges and 9 vertices

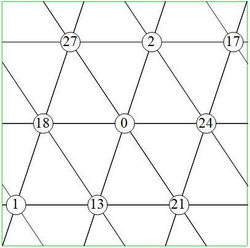
Selected results

  • In his original paper, Rosa proved that an Eulerian graph with number of edges m ≡ 1 (mod 4) or m ≡ 2 (mod 4) cannot be graceful.[2]
  • Also in his original paper, Rosa proved that the cycle Cn is graceful if and only if n ≡ 0 (mod 4) or n ≡ 3 (mod 4).
  • All path graphs and caterpillar graphs are graceful.
  • All lobster graphs with a perfect matching are graceful.[9]
  • All trees with at most 27 vertices are graceful; this result was shown by Aldred and McKay in 1998 using a computer program.[10][11] This was extended to trees with at most 29 vertices in the Honours thesis of Michael Horton.[12] Another extension of this result up to trees with 35 vertices was claimed in 2010 by the Graceful Tree Verification Project, a distributed computing project led by Wenjie Fang.[13]
  • All wheel graphs, web graphs, helm graphs, gear graphs, and rectangular grids are graceful.[10]
  • All n-dimensional hypercubes are graceful.[14]
  • All simple connected graphs with four or fewer vertices are graceful. The only non-graceful simple connected graphs with five vertices are the 5-cycle (pentagon); the complete graph K5; and the butterfly graph.[15]

See also

References

  1. ↑ Virginia Vassilevska, "Coding and Graceful Labeling of trees." SURF 2001. PostScript
  2. ↑ 2.0 2.1 Rosa, A. (1967), "On certain valuations of the vertices of a graph", Theory of Graphs (Internat. Sympos., Rome, 1966), New York: Gordon and Breach, pp. 349–355 .
  3. ↑ Wang, Tao-Ming; Yang, Cheng-Chang; Hsu, Lih-Hsing; Cheng, Eddie (2015), "Infinitely many equivalent versions of the graceful tree conjecture", Applicable Analysis and Discrete Mathematics 9 (1): 1–12, doi:10.2298/AADM141009017W 
  4. ↑ Montgomery, Richard; Pokrovskiy, Alexey; Sudakov, Benny (2020). "A proof of Ringel's Conjecture". arXiv:2001.02665 [math.CO].
  5. ↑ Huang, C.; Kotzig, A.; Rosa, A. (1982), "Further results on tree labellings", Utilitas Mathematica 21: 31–48 .
  6. ↑ Hartnett, Kevin. "Rainbow Proof Shows Graphs Have Uniform Parts" (in en). https://www.quantamagazine.org/mathematicians-prove-ringels-graph-theory-conjecture-20200219/. 
  7. ↑ Huang, C. (1982), "Further results on tree labellings", Utilitas Mathematica 21: 31–48 .
  8. ↑ Rosa, A. (1988), "Cyclic Steiner Triple Systems and Labelings of Triangular Cacti", Scientia 1: 87–95 .
  9. ↑ Morgan, David (2008), "All lobsters with perfect matchings are graceful", Bulletin of the Institute of Combinatorics and Its Applications 53: 82–85 .
  10. ↑ 10.0 10.1 "A dynamic survey of graph labeling", Electronic Journal of Combinatorics 5: Dynamic Survey 6, 43 pp. (389 pp. in 18th ed.) (electronic), 1998, http://www.combinatorics.org/ojs/index.php/eljc/article/viewFile/DS6/pdf .
  11. ↑ Aldred, R. E. L. (1998), "Graceful and harmonious labellings of trees", Bulletin of the Institute of Combinatorics and Its Applications 23: 69–72 .
  12. ↑ Graceful Trees: Statistics and Algorithms, 2003, http://eprints.utas.edu.au/19/ .
  13. ↑ Fang, Wenjie (2010), A Computational Approach to the Graceful Tree Conjecture, Bibcode: 2010arXiv1003.3045F . See also Graceful Tree Verification Project
  14. ↑ "Decompositions of complete graphs into isomorphic cubes", Journal of Combinatorial Theory, Series B 31 (3): 292–296, 1981, doi:10.1016/0095-8956(81)90031-9 .
  15. ↑ Weisstein, Eric W.. "Graceful graph". http://mathworld.wolfram.com/GracefulGraph.html. 

External links

Further reading

  • (K. Eshghi) Introduction to Graceful Graphs, Sharif University of Technology, 2002.
  • (U. N. Deshmukh and Vasanti N. Bhat-Nayak), New families of graceful banana trees – Proceedings Mathematical Sciences, 1996 – Springer
  • (M. Haviar, M. Ivaska), Vertex Labellings of Simple Graphs, Research and Exposition in Mathematics, Volume 34, 2015.
  • (Ping Zhang), A Kaleidoscopic View of Graph Colorings, SpringerBriefs in Mathematics, 2016 – Springer



Retrieved from "https://handwiki.org/wiki/index.php?title=Graceful_labeling&oldid=3381598"