Biology:Steady state (biochemistry)
In biochemistry, steady state refers to the maintenance of constant internal concentrations of molecules and ions in the cells and organs of living systems.[1] Living organisms remain at a dynamic steady state where their internal composition at both cellular and gross levels are relatively constant, but different from equilibrium concentrations.[1] A continuous flux of mass and energy results in the constant synthesis and breakdown of molecules via chemical reactions of biochemical pathways.[1] Essentially, steady state can be thought of as homeostasis at a cellular level.[1]
Maintenance of steady state
Metabolic regulation achieves a balance between the rate of input of a substrate and the rate that it is degraded or converted, and thus maintains steady state.[1] The rate of metabolic flow, or flux, is variable and subject to metabolic demands.[1] However, in a metabolic pathway, steady state is maintained by balancing the rate of substrate provided by a previous step and the rate that the substrate is converted into product, keeping substrate concentration relatively constant.[1]
Thermodynamically speaking, living organisms are open systems, meaning that they constantly exchange matter and energy with their surroundings.[1] A constant supply of energy is required for maintaining steady state, as maintaining a constant concentration of a molecule preserves internal order and thus is entropically unfavorable.[1] When a cell dies and no longer utilizes energy, its internal composition will proceed toward equilibrium with its surroundings.[1]
In some occurrences, it is necessary for cells to adjust their internal composition in order to reach a new steady state.[1] Cell differentiation, for example, requires specific protein regulation that allows the differentiating cell to meet new metabolic requirements.[1]
ATP
The concentration of ATP must be kept above equilibrium level so that the rates of ATP-dependent biochemical reactions meet metabolic demands. A decrease in ATP will result in a decreased saturation of enzymes that use ATP as substrate, and thus a decreased reaction rate.[1] The concentration of ATP is also kept higher than that of AMP, and a decrease in the ATP/AMP ratio triggers AMPK to activate cellular processes that will return ATP and AMP concentrations to steady state.[1]
In one step of the glycolysis pathway catalyzed by PFK-1, the equilibrium constant of reaction is approximately 1000, but the steady state concentration of products (fructose-1,6-bisphosphate and ADP) over reactants (fructose-6-phosphate and ATP) is only 0.1, indicating that the ratio of ATP to AMP remains in a steady state significantly above equilibrium concentration. Regulation of PFK-1 maintains ATP levels above equilibrium.[1]
In the cytoplasm of hepatocytes, the steady state ratio of NADP+ to NADPH is approximately 0.1 while that of NAD+ to NADH is approximately 1000, favoring NADPH as the main reducing agent and NAD+ as the main oxidizing agent in chemical reactions.[2]
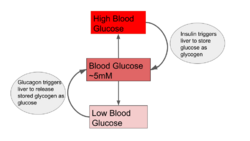
Blood glucose
Blood glucose levels are maintained at a steady state concentration by balancing the rate of entry of glucose into the blood stream (i.e. by ingestion or released from cells) and the rate of glucose uptake by body tissues.[1] Changes in the rate of input will be met with a change in consumption, and vice versa, so that blood glucose concentration is held at about 5 mM in humans.[1] A change in blood glucose levels triggers the release of insulin or glucagon, which stimulates the liver to release glucose into the bloodstream or take up glucose from the bloodstream in order to return glucose levels to steady state.[1] Pancreatic beta cells, for example, increase oxidative metabolism as a result of a rise in blood glucose concentration, triggering secretion of insulin.[3] Glucose levels in the brain are also maintained at steady state, and glucose delivery to the brain relies on the balance between the flux of the blood brain barrier and uptake by brain cells.[4] In teleosts, a drop of blood glucose levels below that of steady state decreases the intracellular-extracellular gradient in the bloodstream, limiting glucose metabolism in red blood cells.[5]
Blood lactate
Blood lactate levels are also maintained at steady state. At rest or low levels of exercise, the rate of lactate production in muscle cells and consumption in muscle or blood cells allows lactate to remain in the body at a certain steady state concentration. If a higher level of exercise is sustained, however, blood lactose levels will increase before becoming constant, indicating that a new steady state of elevated concentration has been reached. Maximal lactate steady state (MLSS) refers to the maximum constant concentration of lactase reached during sustained high-activity.[6]
Nitrogen-containing molecules
Metabolic regulation of nitrogen-containing molecules, such as amino acids, is also kept at steady state.[2] The amino acid pool, which describes the level of amino acids in the body, is maintained at a relatively constant concentration by balancing the rate of input (i.e. from dietary protein ingestion, production of metabolic intermediates) and rate of depletion (i.e. from formation of body proteins, conversion to energy-storage molecules).[2] Amino acid concentration in lymph node cells, for example, is kept at steady state with active transport as the primary source of entry, and diffusion as the source of efflux.[7]
Ions
One main function of plasma and cell membranes is to maintain asymmetric concentrations of inorganic ions in order to maintain an ionic steady state different from electrochemical equilibrium.[8] In other words, there is a differential distribution of ions on either side of the cell membrane - that is, the amount of ions on either side is not equal and therefore a charge separation exists.[8] However, ions move across the cell membrane such that a constant resting membrane potential is achieved; this is ionic steady state.[8] In the pump-leak model of cellular ion homeostasis, energy is utilized to actively transport ions against their electrochemical gradient.[9] The maintenance of this steady state gradient, in turn, is used to do electrical and chemical work, when it is dissipated though the passive movement of ions across the membrane.[9]
In cardiac muscle, ATP is used to actively transport sodium ions out of the cell through a membrane ATPase.[10] Electrical excitation of the cell results in an influx of sodium ions into the cell, temporarily depolarizing the cell.[10] To restore the steady state electrochemical gradient, ATPase removes sodium ions and restores potassium ions in the cell.[10] When an elevated heart rate is sustained, causing more depolarizations, sodium levels in the cell increase until becoming constant, indicating that a new steady state has been reached.[10]
Stability of the steady-state
Steady-states can be stable or unstable. A steady-state is unstable if a small perturbation in one or more of the concentrations results in the system diverging from its state. In contrast, if a steady-state is stable, any perturbation will relax back to the original steady state. Further details can be found on the page Stability theory.
Simple Example
The following provides a simple example for computing the steady-state give a simple mathematical model.
Consider the open chemical system composed of two reactions with rates [math]\displaystyle{ v_1 }[/math]and [math]\displaystyle{ v_2: }[/math]:
[math]\displaystyle{ X_o \stackrel{v_1}{\longrightarrow} S_1 \stackrel{v_2}{\longrightarrow} X_1 }[/math]
We will assume that the chemical species [math]\displaystyle{ X_o }[/math] and [math]\displaystyle{ X_1 }[/math] are fixed external species and [math]\displaystyle{ S_1 }[/math] is an internal chemical species that is allowed to change. The fixed boundaries is to ensure the system can reach a steady-state. If we assume simple irreversible mass-action kinetics, the differential equation describing the concentration of [math]\displaystyle{ S_1 }[/math] is given by:
[math]\displaystyle{ \frac{d S_1}{dt} = k_1 X_o - k_2 S_1 }[/math]
To find the steady-state the differential equation is set to zero and the equation rearranged to solve for [math]\displaystyle{ S_1 }[/math]
[math]\displaystyle{ S_1 = \frac{k_1 X_o}{k_2} }[/math]
This is the steady-state concentration of [math]\displaystyle{ S_1 }[/math].
The stability of this system can be determined by making a perturbation [math]\displaystyle{ \delta S_1 }[/math] in [math]\displaystyle{ S_1 }[/math] This can be expressed as:
[math]\displaystyle{ \frac{d (S_1 + \delta S_1)}{dt} = k_1 X_o - k_2 (S_1 + \delta S_1) }[/math]
Note that the [math]\displaystyle{ \delta S_1 }[/math] will elicit a change in the rate of change. At steady-state [math]\displaystyle{ k_1 X_o - k_2 S_1 = 0 }[/math], therefore the rate of change of [math]\displaystyle{ S_1 }[/math] as a result of this perturbation is:
[math]\displaystyle{ \frac{d \delta S_1}{dt} = - k_2 \delta S_1 }[/math]
This shows that the perturbation, [math]\displaystyle{ \delta S_1 }[/math] decays exponetially, hence the system is stable.
See also
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 Nelson, David L. (David Lee), 1942- (2008). Lehninger principles of biochemistry. Nelson, David L. (David Lee), 1942-, Lehninger, Albert L., Cox, Michael M. (5th ed.). New York: W.H. Freeman. ISBN 978-0716771081. OCLC 191854286. https://archive.org/details/lehningerprincip00lehn_1.
- ↑ 2.0 2.1 2.2 Harvey, Richard A., Ph. D. (2011). Biochemistry. Ferrier, Denise R. (5th ed.). Philadelphia: Wolters Kluwer Health/Lippincott Williams & Wilkins. ISBN 9781608314126. OCLC 551719648.
- ↑ Fridlyand, Leonid E.; Phillipson, Louis H. (September 2011). "Mechanisms of glucose sensing in the pancreatic β-cell: A computational systems-based analysis". Islets 3 (5): 224–230. doi:10.4161/isl.3.5.16409. ISSN 1938-2022. PMID 21814042.
- ↑ Leybaert, Luc; De Bock, Marijke; Van Moorhem, Marijke; Decrock, Elke; De Vuyst, Elke (2007-11-15). "Neurobarrier coupling in the brain: adjusting glucose entry with demand". Journal of Neuroscience Research 85 (15): 3213–3220. doi:10.1002/jnr.21189. ISSN 0360-4012. PMID 17265466.
- ↑ Driedzic, William R. (October 2018). "Low plasma glucose limits glucose metabolism by RBCs and heart in some species of teleosts". Comparative Biochemistry and Physiology. Part B, Biochemistry & Molecular Biology 224: 204–209. doi:10.1016/j.cbpb.2017.08.002. ISSN 1879-1107. PMID 28803129.
- ↑ Billat, Véronique L.; Sirvent, Pascal; Py, Guillaume; Koralsztein, Jean-Pierre; Mercier, Jacques (2003-05-01). "The Concept of Maximal Lactate Steady State". Sports Medicine 33 (6): 407–426. doi:10.2165/00007256-200333060-00003. ISSN 1179-2035. PMID 12744715.
- ↑ Helmreich, E.; Kipnis, D. M. (August 1962). "Amino acid transport in lymph node cells". The Journal of Biological Chemistry 237 (8): 2582–2589. doi:10.1016/S0021-9258(19)73792-2. ISSN 0021-9258. PMID 13906342.
- ↑ 8.0 8.1 8.2 Dubyak, George R. (December 2004). "Ion homeostasis, channels, and transporters: an update on cellular mechanisms". Advances in Physiology Education 28 (4): 143–154. doi:10.1152/advan.00046.2004. ISSN 1043-4046. PMID 15545343.
- ↑ 9.0 9.1 Physiology and Pathology of Chloride Transporters and Channels in the Nervous System. 2010. doi:10.1016/b978-0-12-374373-2.x0001-5. ISBN 9780123743732.
- ↑ 10.0 10.1 10.2 10.3 LANGER, G. A. (July 1972). "Effects of Digitalis on Myocardial Ionic Exchange". Circulation 46 (1): 180–187. doi:10.1161/01.cir.46.1.180. ISSN 0009-7322. PMID 4263007.
 |