Physics:Thermodynamic system
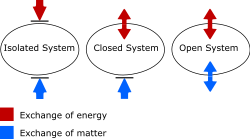
A thermodynamic system is a body of matter and/or radiation separate from its surroundings that can be studied using the laws of thermodynamics. A thermodynamic system may be an isolated system, a closed system, or an open system. An isolated system does not exchange matter or energy with its surroundings. A closed system may exchange heat, experience forces, and exert forces, but does not exchange matter. An open system can interact with its surroundings by exchanging both matter and energy.
The physical condition of a thermodynamic system at a given time is described by its state, which can be specified by the values of a set of thermodynamic state variables. A thermodynamic system is in thermodynamic equilibrium when there are no macroscopically apparent flows of matter or energy within it or between it and other systems.[1]

Overview
| Thermodynamics |
|---|
 |
Thermodynamic equilibrium is characterized by absence of flow of mass or energy. Equilibrium thermodynamics, as a subject in physics, considers macroscopic bodies of matter and energy in states of internal thermodynamic equilibrium. It uses the concept of thermodynamic processes, by which bodies pass from one equilibrium state to another by transfer of matter and energy between them. The term 'thermodynamic system' is used to refer to bodies of matter and energy in the special context of thermodynamics. The possible equilibria between bodies are determined by the physical properties of the walls that separate the bodies. Equilibrium thermodynamics in general does not measure time. Equilibrium thermodynamics is a relatively simple and well settled subject. One reason for this is the existence of a well defined physical quantity called 'the entropy of a body'.
Non-equilibrium thermodynamics, as a subject in physics, considers bodies of matter and energy that are not in states of internal thermodynamic equilibrium, but are usually participating in processes of transfer that are slow enough to allow description in terms of quantities that are closely related to thermodynamic state variables. It is characterized by presence of flows of matter and energy. For this topic, very often the bodies considered have smooth spatial inhomogeneities, so that spatial gradients, for example a temperature gradient, are well enough defined. Thus the description of non-equilibrium thermodynamic systems is a field theory, more complicated than the theory of equilibrium thermodynamics. Non-equilibrium thermodynamics is a growing subject, not an established edifice. In general, it is not possible to find an exactly defined entropy for non-equilibrium problems. For many non-equilibrium thermodynamical problems, an approximately defined quantity called 'time rate of entropy production' is very useful. Non-equilibrium thermodynamics is mostly beyond the scope of the present article.
Another kind of thermodynamic system is considered in most engineering. It takes part in a flow process. The account is in terms that approximate, well enough in practice in many cases, equilibrium thermodynamical concepts. This is mostly beyond the scope of the present article, and is set out in other articles, for example the article Flow process.
History
The first to create the concept of a thermodynamic system was the French physicist Sadi Carnot whose 1824 Reflections on the Motive Power of Fire studied what he called the working substance, e.g., typically a body of water vapor, in steam engines, in regards to the system's ability to do work when heat is applied to it. The working substance could be put in contact with either a heat reservoir (a boiler), a cold reservoir (a stream of cold water), or a piston (to which the working body could do work by pushing on it). In 1850, the German physicist Rudolf Clausius generalized this picture to include the concept of the surroundings, and began referring to the system as a "working body". In his 1850 paper On the Motive Power of Heat, Clausius wrote:
| “ | With every change of volume (to the working body) a certain amount work must be done by the gas or upon it, since by its expansion it overcomes an external pressure, and since its compression can be brought about only by an exertion of external pressure. To this excess of work done by the gas or upon it there must correspond, by our principle, a proportional excess of heat consumed or produced, and the gas cannot give up to the "surrounding medium" the same amount of heat as it receives. | ” |
The article Carnot heat engine shows the original piston-and-cylinder diagram used by Carnot in discussing his ideal engine; below, we see the Carnot engine as is typically modeled in current use:

In the diagram shown, the "working body" (system), a term introduced by Clausius in 1850, can be any fluid or vapor body through which heat Q can be introduced or transmitted through to produce work. In 1824, Sadi Carnot, in his famous paper Reflections on the Motive Power of Fire, had postulated that the fluid body could be any substance capable of expansion, such as vapor of water, vapor of alcohol, vapor of mercury, a permanent gas, or air, etc. Though, in these early years, engines came in a number of configurations, typically QH was supplied by a boiler, wherein water boiled over a furnace; QC was typically a stream of cold flowing water in the form of a condenser located on a separate part of the engine. The output work W was the movement of the piston as it turned a crank-arm, which typically turned a pulley to lift water out of flooded salt mines. Carnot defined work as "weight lifted through a height".
Systems in equilibrium
In isolated systems it is consistently observed that as time goes on internal rearrangements diminish and stable conditions are approached. Pressures and temperatures tend to equalize, and matter arranges itself into one or a few relatively homogeneous phases. A system in which all processes of change have gone practically to completion is considered in a state of thermodynamic equilibrium.[2] The thermodynamic properties of a system in equilibrium are unchanging in time. Equilibrium system states are much easier to describe in a deterministic manner than non-equilibrium states. In some cases, when analyzing a thermodynamic process, one can assume that each intermediate state in the process is at equilibrium. Such a process is called quasistatic.[3]
For a process to be reversible, each step in the process must be reversible. For a step in a process to be reversible, the system must be in equilibrium throughout the step. That ideal cannot be accomplished in practice because no step can be taken without perturbing the system from equilibrium, but the ideal can be approached by making changes slowly.
The very existence of thermodynamic equilibrium, defining states of thermodynamic systems, is the essential, characteristic, and most fundamental postulate of thermodynamics, though it is only rarely cited as a numbered law.[4][5][6] According to Bailyn, the commonly rehearsed statement of the zeroth law of thermodynamics is a consequence of this fundamental postulate.[7] In reality, practically nothing in nature is in strict thermodynamic equilibrium, but the postulate of thermodynamic equilibrium often provides very useful idealizations or approximations, both theoretically and experimentally; experiments can provide scenarios of practical thermodynamic equilibrium.
In equilibrium thermodynamics the state variables do not include fluxes because in a state of thermodynamic equilibrium all fluxes have zero values by definition. Equilibrium thermodynamic processes may involve fluxes but these must have ceased by the time a thermodynamic process or operation is complete bringing a system to its eventual thermodynamic state. Non-equilibrium thermodynamics allows its state variables to include non-zero fluxes, which describe transfers of mass or energy or entropy between a system and its surroundings.[8]
Walls
| type of wall | type of transfer | ||
|---|---|---|---|
| Matter | Work | Heat | |
| permeable to matter | |||
| permeable to energy but
impermeable to matter |
|||
| adiabatic | |||
| adynamic and
impermeable to matter |
|||
| isolating | |||
A system is enclosed by walls that bound it and connect it to its surroundings.[9][10][11][12][13] Often a wall restricts passage across it by some form of matter or energy, making the connection indirect. Sometimes a wall is no more than an imaginary two-dimensional closed surface through which the connection to the surroundings is direct.
A wall can be fixed (e.g. a constant volume reactor) or moveable (e.g. a piston). For example, in a reciprocating engine, a fixed wall means the piston is locked at its position; then, a constant volume process may occur. In that same engine, a piston may be unlocked and allowed to move in and out. Ideally, a wall may be declared adiabatic, diathermal, impermeable, permeable, or semi-permeable. Actual physical materials that provide walls with such idealized properties are not always readily available.
The system is delimited by walls or boundaries, either actual or notional, across which conserved (such as matter and energy) or unconserved (such as entropy) quantities can pass into and out of the system. The space outside the thermodynamic system is known as the surroundings, a reservoir, or the environment. The properties of the walls determine what transfers can occur. A wall that allows transfer of a quantity is said to be permeable to it, and a thermodynamic system is classified by the permeabilities of its several walls. A transfer between system and surroundings can arise by contact, such as conduction of heat, or by long-range forces such as an electric field in the surroundings.
A system with walls that prevent all transfers is said to be isolated. This is an idealized conception, because in practice some transfer is always possible, for example by gravitational forces. It is an axiom of thermodynamics that an isolated system eventually reaches internal thermodynamic equilibrium, when its state no longer changes with time.
The walls of a closed system allow transfer of energy as heat and as work, but not of matter, between it and its surroundings. The walls of an open system allow transfer both of matter and of energy.[14][15][16][17][18][19][20] This scheme of definition of terms is not uniformly used, though it is convenient for some purposes. In particular, some writers use 'closed system' where 'isolated system' is here used.[21][22]
Anything that passes across the boundary and effects a change in the contents of the system must be accounted for in an appropriate balance equation. The volume can be the region surrounding a single atom resonating energy, such as Max Planck defined in 1900; it can be a body of steam or air in a steam engine, such as Sadi Carnot defined in 1824. It could also be just one nuclide (i.e. a system of quarks) as hypothesized in quantum thermodynamics.
Surroundings
The system is the part of the universe being studied, while the surroundings is the remainder of the universe that lies outside the boundaries of the system. It is also known as the environment or the reservoir. Depending on the type of system, it may interact with the system by exchanging mass, energy (including heat and work), momentum, electric charge, or other conserved properties. The environment is ignored in the analysis of the system, except in regards to these interactions.
Closed system
In a closed system, no mass may be transferred in or out of the system boundaries. The system always contains the same amount of matter, but (sensible) heat and (boundary) work can be exchanged across the boundary of the system. Whether a system can exchange heat, work, or both is dependent on the property of its boundary.
- Adiabatic boundary – not allowing any heat exchange: A thermally isolated system
- Rigid boundary – not allowing exchange of work: A mechanically isolated system
One example is fluid being compressed by a piston in a cylinder. Another example of a closed system is a bomb calorimeter, a type of constant-volume calorimeter used in measuring the heat of combustion of a particular reaction. Electrical energy travels across the boundary to produce a spark between the electrodes and initiates combustion. Heat transfer occurs across the boundary after combustion but no mass transfer takes place either way.
The first law of thermodynamics for energy transfers for closed system may be stated:
where denotes the internal energy of the system, heat added to the system, the work done by the system. For infinitesimal changes the first law for closed systems may stated:
If the work is due to a volume expansion by at a pressure then:
For a quasi-reversible heat transfer, the second law of thermodynamics reads:
where denotes the thermodynamic temperature and the entropy of the system. With these relations the fundamental thermodynamic relation, used to compute changes in internal energy, is expressed as:
For a simple system, with only one type of particle (atom or molecule), a closed system amounts to a constant number of particles. For systems undergoing a chemical reaction, there may be all sorts of molecules being generated and destroyed by the reaction process. In this case, the fact that the system is closed is expressed by stating that the total number of each elemental atom is conserved, no matter what kind of molecule it may be a part of. Mathematically:
where denotes the number of -type molecules, the number of atoms of element in molecule , and the total number of atoms of element in the system, which remains constant, since the system is closed. There is one such equation for each element in the system.
Isolated system
An isolated system is more restrictive than a closed system as it does not interact with its surroundings in any way. Mass and energy remains constant within the system, and no energy or mass transfer takes place across the boundary. As time passes in an isolated system, internal differences in the system tend to even out and pressures and temperatures tend to equalize, as do density differences. A system in which all equalizing processes have gone practically to completion is in a state of thermodynamic equilibrium.
Truly isolated physical systems do not exist in reality (except perhaps for the universe as a whole), because, for example, there is always gravity between a system with mass and masses elsewhere.[23][24][25][26][27] However, real systems may behave nearly as an isolated system for finite (possibly very long) times. The concept of an isolated system can serve as a useful model approximating many real-world situations. It is an acceptable idealization used in constructing mathematical models of certain natural phenomena.
In the attempt to justify the postulate of entropy increase in the second law of thermodynamics, Boltzmann's H-theorem used equations, which assumed that a system (for example, a gas) was isolated. That is all the mechanical degrees of freedom could be specified, treating the walls simply as mirror boundary conditions. This inevitably led to Loschmidt's paradox. However, if the stochastic behavior of the molecules in actual walls is considered, along with the randomizing effect of the ambient, background thermal radiation, Boltzmann's assumption of molecular chaos can be justified.
The second law of thermodynamics for isolated systems states that the entropy of an isolated system not in equilibrium tends to increase over time, approaching maximum value at equilibrium. Overall, in an isolated system, the internal energy is constant and the entropy can never decrease. A closed system's entropy can decrease e.g. when heat is extracted from the system.
Isolated systems are not equivalent to closed systems. Closed systems cannot exchange matter with the surroundings, but can exchange energy. Isolated systems can exchange neither matter nor energy with their surroundings, and as such are only theoretical and do not exist in reality (except, possibly, the entire universe).
'Closed system' is often used in thermodynamics discussions when 'isolated system' would be correct – i.e. there is an assumption that energy does not enter or leave the system.
Selective transfer of matter
For a thermodynamic process, the precise physical properties of the walls and surroundings of the system are important, because they determine the possible processes.
An open system has one or several walls that allow transfer of matter. To account for the internal energy of the open system, this requires energy transfer terms in addition to those for heat and work. It also leads to the idea of the chemical potential.
A wall selectively permeable only to a pure substance can put the system in diffusive contact with a reservoir of that pure substance in the surroundings. Then a process is possible in which that pure substance is transferred between system and surroundings. Also, across that wall a contact equilibrium with respect to that substance is possible. By suitable thermodynamic operations, the pure substance reservoir can be dealt with as a closed system. Its internal energy and its entropy can be determined as functions of its temperature, pressure, and mole number.
A thermodynamic operation can render impermeable to matter all system walls other than the contact equilibrium wall for that substance. This allows the definition of an intensive state variable, with respect to a reference state of the surroundings, for that substance. The intensive variable is called the chemical potential; for component substance i it is usually denoted μi. The corresponding extensive variable can be the number of moles Ni of the component substance in the system.
For a contact equilibrium across a wall permeable to a substance, the chemical potentials of the substance must be same on either side of the wall. This is part of the nature of thermodynamic equilibrium, and may be regarded as related to the zeroth law of thermodynamics.[28]
Open system
In an open system, there is an exchange of energy and matter between the system and the surroundings. The presence of reactants in an open beaker is an example of an open system. Here the boundary is an imaginary surface enclosing the beaker and reactants. It is named closed, if borders are impenetrable for substance, but allow transit of energy in the form of heat, and isolated, if there is no exchange of heat and substances. The open system cannot exist in the equilibrium state. To describe deviation of the thermodynamic system from equilibrium, in addition to constitutive variables that was described above, a set of internal variables have been introduced. The equilibrium state is considered to be stable and the main property of the internal variables, as measures of non-equilibrium of the system, is their trending to disappear; the local law of disappearing can be written as relaxation equation for each internal variable
-
()
where is a relaxation time of a corresponding variable. It is convenient to consider the initial value equal to zero.
The specific contribution to the thermodynamics of open non-equilibrium systems was made by Ilya Prigogine, who investigated a system of chemically reacting substances.[29] In this case the internal variables appear to be measures of incompleteness of chemical reactions, that is measures of how much the considered system with chemical reactions is out of equilibrium. The theory can be generalized,[30][31][32] to consider any deviations from the equilibrium state, such as structure of the system, gradients of temperature, difference of concentrations of substances and so on, to say nothing of degrees of completeness of all chemical reactions, to be internal variables.
The increments of Gibbs free energy and entropy at and are determined as
-
()
-
()
The stationary states of the system exist due to exchange of both thermal energy and a stream of particles. The sum of the last terms in the equations presents the total energy coming into the system with the stream of particles of substances that can be positive or negative; the quantity is chemical potential of substance . The middle terms in equations (2) and (3) depict energy dissipation (entropy production) due to the relaxation of internal variables , while are thermodynamic forces.
This approach to the open system allows describing the growth and development of living objects in thermodynamic terms.[33]
See also
- Dynamical system
- Energy system
- Isolated system
- Mechanical system
- Physical system
- Quantum system
- Thermodynamic cycle
- Thermodynamic process
- Two-state quantum system
References
- ↑ Rex & Finn 2017, p. 1–4.
- ↑ Rex & Finn 2017, p. 1–2.
- ↑ Rex & Finn 2017, p. 20.
- ↑ Bailyn 1994, p. 20.
- ↑ Tisza 1966, p. 119.
- ↑ Marsland, R. III, Brown, H.R., Valente, G. (2015). Time and irreversibility in axiomatic thermodynamics, Am. J. Phys., 83(7): 628–634.
- ↑ Bailyn 1994, p. 22.
- ↑ Eu, B.C. (2002). Generalized Thermodynamics. The Thermodynamics of Irreversible Processes and Generalized Hydrodynamics, Kluwer Academic Publishers, Dordrecht, ISBN:1-4020-0788-4.
- ↑ Born, M. (1949). Natural Philosophy of Cause and Chance, Oxford University Press, London, p.44
- ↑ Tisza 1966, p. 109, 112.
- ↑ Haase 1971, p. 7.
- ↑ Callen 1985, p. 15, 17.
- ↑ Tschoegl 2000, p. 5.
- ↑ Prigogine, I., Defay, R. (1950/1954). Chemical Thermodynamics, Longmans, Green & Co, London, p. 66.
- ↑ Tisza 1966, p. 112–113.
- ↑ Guggenheim, E.A. (1949/1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, (1st edition 1949) 5th edition 1967, North-Holland, Amsterdam, p. 14.
- ↑ Münster, A. (1970). Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, pp. 6–7.
- ↑ Haase 1971, p. 1–97.
- ↑ Tschoegl 2000, p. 3.
- ↑ Silbey, R.J., Alberty, R.A., Bawendi, M.G. (1955/2005). Physical Chemistry, fourth edition, Wiley, Hoboken NJ, p. 4.
- ↑ Callen 1985, p. 17.
- ↑ ter Haar, D., Wergeland, H. (1966). Elements of Thermodynamics, Addison-Wesley Publishing, Reading MA, p. 43.
- ↑ I.M.Kolesnikov; V.A.Vinokurov; S.I.Kolesnikov (2001). Thermodynamics of Spontaneous and Non-Spontaneous Processes. Nova science Publishers. p. 136. ISBN 978-1-56072-904-4. https://books.google.com/books?id=2RzE2pCfijYC&pg=PA136.
- ↑ "A System and Its Surroundings". University of California - Davis. http://chemwiki.ucdavis.edu/Physical_Chemistry/Thermodynamics/A_System_And_Its_Surroundings#Isolated_System.
- ↑ "Hyperphysics". The Department of Physics and Astronomy of Georgia State University. http://hyperphysics.phy-astr.gsu.edu/hbase/conser.html#isosys.
- ↑ Bryan Sanctuary. "Open, Closed and Isolated Systems in Physical Chemistry". McGill University (Montreal). http://quantummechanics.mchmultimedia.com/2011/physical-chemistry/open-closed-and-isolated-systems-in-chemistry/.
- ↑ Material and Energy Balances for Engineers and Environmentalists. Imperial College Press. p. 7. http://www.icpress.co.uk/etextbook/p631/p631_chap01.pdf. Retrieved 9 May 2012.
- ↑ Bailyn 1994, p. 19–23.
- ↑ Prigogine, I. (1955/1961/1967). Introduction to Thermodynamics of Irreversible Processes. 3rd edition, Wiley Interscience, New York.
- ↑ Pokrovskii V.N. (2005) Extended thermodynamics in a discrete-system approach, Eur. J. Phys. vol. 26, 769–781.
- ↑ Pokrovskii V.N. (2013) A derivation of the main relations of non-equilibrium thermodynamics. Hindawi Publishing Corporation: ISRN Thermodynamics, vol. 2013, article ID 906136, 9 p. https://dx.doi.org/10.1155/2013/906136.
- ↑ Pokrovskii, Vladimir (2020) (in English). Thermodynamics of Complex Systems: Principles and applications.. IOP Publishing, Bristol, UK.. Bibcode: 2020tcsp.book.....P.
- ↑ Zotin, Alexei; Pokrovskii, Vladimir (2018). "The growth and development of living organisms from the thermodynamic point of view". Physica A: Statistical Mechanics and Its Applications 512: 359–366. doi:10.1016/j.physa.2018.08.094. Bibcode: 2018PhyA..512..359Z.
Sources
- Abbott, M.M.; van Hess, H. G. (1989). Thermodynamics with Chemical Applications (2nd ed.). McGraw Hill.
- Bailyn, M. (1994). A Survey of Thermodynamics. New York: American Institute of Physics Press. ISBN 0-88318-797-3.
- Callen, H. B. (1985). Thermodynamics and an Introduction to Thermostatistics (2nd ed.). New York: Wiley. ISBN 0-471-86256-8.
- Haase, R. (1971). "Survey of Fundamental Laws". Thermodynamics. Physical Chemistry: An Advanced Treatise. 1. New York: Academic Press. pp. 1–97.
- Halliday, David; Resnick, Robert; Walker, Jearl (2008). Fundamentals of Physics (8th ed.). Wiley.
- Moran, Michael J.; Shapiro, Howard N. (2008). Fundamentals of Engineering Thermodynamics (6th ed.). Wiley.
- Rex, Andrew; Finn, C. B. P. (2017). Finn's Thermal Physics (3rd ed.). Taylor & Francis. ISBN 978-1-498-71887-5.
- Tisza, László (1966). Generalized Thermodynamics. MIT Press.
- Tschoegl, N. W. (2000). Fundamentals of Equilibrium and Steady-State Thermodynamics. Amsterdam: Elsevier. ISBN 0-444-50426-5.
 |

